Kącik początkującego olimpijczyka
Jak przechytrzyć stereometrię
Rozpatrując siatkę, odpowiedni przekrój lub rzut, możemy niekiedy sprowadzić zadanie z geometrii przestrzennej do zadania z planimetrii.
Zadania z geometrii przestrzennej potrafią przysporzyć problemów, ale niektóre z nich można z powodzeniem sprowadzić do zadań z planimetrii. Najprotszą metodą jest rozważenie pewnego przekroju danej w zadaniu bryły. Jeśli zauważymy, że sporo punktów występujących w treści zadania leży na wspólnej płaszczyźnie, to rozważenie przekroju tą płaszczyzną daje realne szanse na rozwiązanie. Ćwiczymy to w zadaniach 1 i 2. Dobrze jest wykonać osobny rysunek dla wybranego przekroju - można wtedy więcej dostrzec.
W szkole składamy wielościany z ich siatek. Czasem warto zrobić na odwrót, a wtedy z obiektu przestrzennego otrzymamy łatwiejszy do analizy obiekt płaski. Takie podejście przynosi efekt w zadaniach 4 i 6. W szczególności dobrym pomysłem jest wyprostowanie pewnego kąta dwuściennego wielościanu, co pozwala dwie sąsiednie ściany i ich wspólną krawędź potraktować jako wielokąt i przekątną. Zadania 3 i 5 nadają się do tego wyśmienicie.
Rzut prostokątny na płaszczyznę 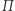 jest przekształceniem, w którym każdemu punktowi
jest przekształceniem, w którym każdemu punktowi 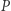 przyporządkujemy taki punkt
przyporządkujemy taki punkt 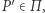 że
że 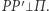 Jeśli
Jeśli 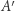 i
i 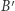 są rzutami prostokątnymi punktów, odpowiednio,
są rzutami prostokątnymi punktów, odpowiednio, 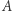 i
i 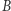 na płaszczyznę
na płaszczyznę 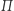 oraz prosta
oraz prosta 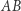 przecina tę płaszczyznę w punkcie
przecina tę płaszczyznę w punkcie 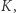 to trójkąty prostokątne
to trójkąty prostokątne 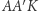 i
i 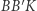 są podobne, a ponadto punkty
są podobne, a ponadto punkty 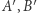 i
i 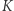 leżą na jednej prostej. Można zrobić z tego użytek, rozwiązując zadania 7 i 8.
leżą na jednej prostej. Można zrobić z tego użytek, rozwiązując zadania 7 i 8.