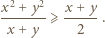Jego Wysokości (I)»Zadanie 2
o zadaniu...
- Zadanie pochodzi z artykułu Jego Wysokości (I)
- Publikacja w Delcie: wrzesień 2020
- Publikacja elektroniczna: 31 sierpnia 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (379 KB)
Udowodnić, że punkty 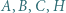 tworzą układ ortocentryczny, jeśli:
tworzą układ ortocentryczny, jeśli:
- (a)
- czworokąty
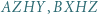 i
i 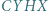 są rombami (kolejność wierzchołków niekoniecznie podana antyzegarowo);
są rombami (kolejność wierzchołków niekoniecznie podana antyzegarowo); - (b)
- przez punkt
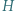 przechodzą trzy okręgi o jednakowych promieniach, a punkty
przechodzą trzy okręgi o jednakowych promieniach, a punkty 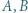 i
i 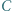 są różnymi od
są różnymi od 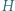 punktami przecięć tych okręgów;
punktami przecięć tych okręgów; - (c)
- punkt
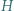 jest środkiem okręgu wpisanego w pewien trójkąt, a punkty
jest środkiem okręgu wpisanego w pewien trójkąt, a punkty 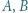 i
i 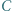 - środkami okręgów dopisanych do niego.
- środkami okręgów dopisanych do niego.
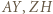 i
i 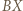 są równej długości i równoległe, więc czworokąt
są równej długości i równoległe, więc czworokąt 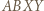 jest równoległobokiem. Mamy więc
jest równoległobokiem. Mamy więc 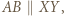 ale też
ale też 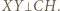
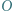 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 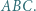 Punkty
Punkty 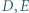 i
i 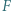 są symetryczne do punktu
są symetryczne do punktu 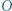 względem prostych odpowiednio
względem prostych odpowiednio 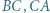 i
i 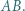 Dowieść, że punkt
Dowieść, że punkt 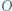 jest ortocentrum trójkąta
jest ortocentrum trójkąta 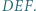
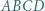 jest wpisany w okrąg. Punkty
jest wpisany w okrąg. Punkty 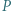 i
i 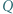 są ortocentrami trójkątów odpowiednio
są ortocentrami trójkątów odpowiednio 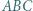 i
i 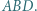 Udowodnić, że
Udowodnić, że 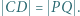
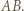 Okrąg o średnicy
Okrąg o średnicy 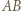 przecina proste
przecina proste 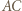 i
i 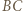 w punktach, które są spodkami wysokości trójkąta
w punktach, które są spodkami wysokości trójkąta 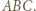
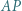 i
i 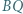 są wysokościami trójkąta nieprostokątnego
są wysokościami trójkąta nieprostokątnego 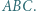 Punkty
Punkty 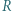 i
i 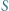 są rzutami prostokątnymi punktów odpowiednio
są rzutami prostokątnymi punktów odpowiednio 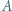 i
i 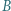 na prostą
na prostą 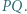 Udowodnić, że
Udowodnić, że 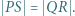
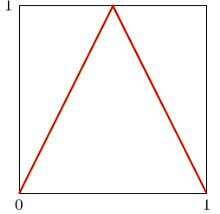
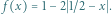
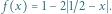
![| f [0,1] [0,1]](/math/temat/matematyka/analiza/zadania/2020/08/26/zm-20-09-gr-2/1x-6ef1c75cd7890fac5a5a10e6c2a3afccfa359dba-im-2C,6B,73-FF,FF,FF.gif) będzie dane wzorem
będzie dane wzorem 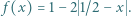 Niech ponadto
Niech ponadto 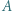 oraz
oraz 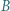 będą dowolnymi niepustymi przedziałami (otwartymi lub domkniętymi jedno- lub obustronnie), których końce są liczbami niewymiernymi. Uzasadnić, że istnieje takie
będą dowolnymi niepustymi przedziałami (otwartymi lub domkniętymi jedno- lub obustronnie), których końce są liczbami niewymiernymi. Uzasadnić, że istnieje takie 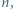 że
że 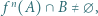 gdzie
gdzie 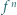 oznacza
oznacza  -krotne złożenie funkcji
-krotne złożenie funkcji 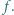
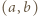 ma tę własność, że
ma tę własność, że ![fn((a,b)) = [0,1]](/math/temat/matematyka/analiza/zadania/2020/08/26/zm-20-09-gr-2/2x-3582530a21981c4662de24aae4547af0402ec105-im-66,57,43-FF,FF,FF.gif) dla pewnego
dla pewnego 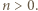 Niech
Niech 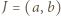 i
i 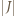 będzie długością tego przedziału. Zauważmy, że jeżeli
będzie długością tego przedziału. Zauważmy, że jeżeli 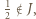 to
to 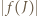 jest przedziałem dwukrotnie dłuższym niż
jest przedziałem dwukrotnie dłuższym niż 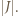 Tym samym kolejne przekształcenia
Tym samym kolejne przekształcenia 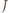 przez
przez 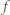 są przedziałami długości
są przedziałami długości 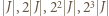 i tak dalej, o ile do żadnego z wymienionych zbiorów nie należy
i tak dalej, o ile do żadnego z wymienionych zbiorów nie należy 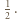 Wobec powyższego istnieje takie
Wobec powyższego istnieje takie 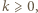 że
że 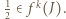 Ale
Ale 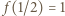 i
i 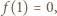 czyli
czyli 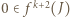 i wobec tego
i wobec tego 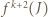 jest przedziałem postaci
jest przedziałem postaci 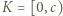 dla pewnego
dla pewnego 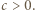 Teraz
Teraz 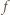 ponownie podwaja długość przedziału
ponownie podwaja długość przedziału 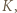 wobec tego dla pewnego
wobec tego dla pewnego 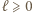 zachodzi
zachodzi 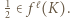 Tym samym
Tym samym ![[0, | 1/2]⊂ fℓ(K)](/math/temat/matematyka/analiza/zadania/2020/08/26/zm-20-09-gr-2/25x-3582530a21981c4662de24aae4547af0402ec105-im-66,57,43-FF,FF,FF.gif) i wystarczy jeszcze zauważyć, że
i wystarczy jeszcze zauważyć, że![[0,1] = f ([0,1/2]) ⊂ fℓ+1(K) = fℓ+1( fk+2(J)) = fk+ℓ+3(J).](/math/temat/matematyka/analiza/zadania/2020/08/26/zm-20-09-gr-2/26x-3582530a21981c4662de24aae4547af0402ec105-dm-66,57,43-FF,FF,FF.gif)
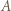 postulowany w treści zadania zawiera w sobie przedział otwarty oraz jeśli
postulowany w treści zadania zawiera w sobie przedział otwarty oraz jeśli 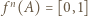 z przypadku ogólnego, to tym bardziej
z przypadku ogólnego, to tym bardziej 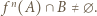
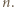
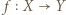 nazywamy iniekcją (funkcją różnowartościową), jeśli z warunku
nazywamy iniekcją (funkcją różnowartościową), jeśli z warunku 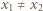 wynika, że
wynika, że 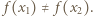 Funkcję
Funkcję 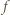 nazywamy surjekcją (funkcją na), gdy dla dowolnego
nazywamy surjekcją (funkcją na), gdy dla dowolnego 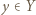 istnieje
istnieje 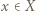 takie, że
takie, że 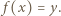 Funkcja, która jest jednocześnie iniekcją i surjekcją, to bijekcja.
Funkcja, która jest jednocześnie iniekcją i surjekcją, to bijekcja. jest skończony, gdy istnieje liczba
jest skończony, gdy istnieje liczba  oraz bijekcja między zbiorami
oraz bijekcja między zbiorami  oraz
oraz 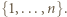 Piszemy wtedy również
Piszemy wtedy również 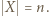
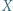 będzie zbiorem skończonym. Udowodnić, że dowolna iniekcja
będzie zbiorem skończonym. Udowodnić, że dowolna iniekcja 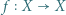 jest bijekcją.
jest bijekcją.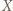 oraz
oraz 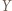 są zbiorami skończonymi o tej samej liczbie elementów oraz
są zbiorami skończonymi o tej samej liczbie elementów oraz 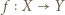 jest iniekcją, to
jest iniekcją, to 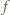 jest bijekcją. Rozwiązanie przebiega indukcyjnie ze względu na liczbę
jest bijekcją. Rozwiązanie przebiega indukcyjnie ze względu na liczbę 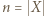 elementów zbioru
elementów zbioru 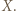 Oczywiście przypadek
Oczywiście przypadek 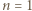 jest spełniony, przechodzimy zatem do kroku indukcyjnego. Niech
jest spełniony, przechodzimy zatem do kroku indukcyjnego. Niech 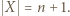 Niech
Niech 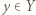 będzie takie, że
będzie takie, że 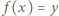 dla pewnego
dla pewnego 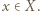 Takie
Takie 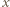 jest jedyne na mocy iniektywności, zatem można rozważyć funkcję
jest jedyne na mocy iniektywności, zatem można rozważyć funkcję 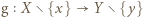 daną wzorem
daną wzorem 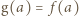 dla
dla 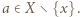 Wtedy
Wtedy 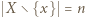 oraz
oraz 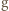 jest iniekcją. Istotnie, jeżeli
jest iniekcją. Istotnie, jeżeli 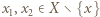 i
i 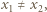 to
to 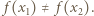 Zauważmy teraz, że
Zauważmy teraz, że 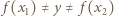 (ponownie korzystamy z iniektywności), zatem również
(ponownie korzystamy z iniektywności), zatem również 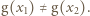 Tym samym
Tym samym 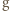 jest iniekcją, a więc z założenia indukcyjnego jest ona bijekcją. Stąd już łatwo wynika, że
jest iniekcją, a więc z założenia indukcyjnego jest ona bijekcją. Stąd już łatwo wynika, że 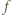 jest bijekcją (dorzucamy po różnym od pozostałych punkcie do dziedziny i przeciwdziedziny).
jest bijekcją (dorzucamy po różnym od pozostałych punkcie do dziedziny i przeciwdziedziny).
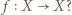 Usunięcie jednego elementu z dziedziny i przeciwdziedziny nie gwarantuje, że dziedzina i przeciwdziedzina
Usunięcie jednego elementu z dziedziny i przeciwdziedziny nie gwarantuje, że dziedzina i przeciwdziedzina 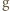 będą tym samym zbiorem, a tylko wtedy moglibyśmy skorzystać z założenia indukcyjnego!
będą tym samym zbiorem, a tylko wtedy moglibyśmy skorzystać z założenia indukcyjnego!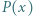 będzie wielomianem
będzie wielomianem 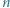 -tego stopnia
-tego stopnia 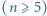 o współczynnikach całkowitych, mającym
o współczynnikach całkowitych, mającym 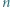 różnych pierwiastków całkowitych. Załóżmy, że 0 jest jednym z jego pierwiastków. Udowodnić, że wielomian
różnych pierwiastków całkowitych. Załóżmy, że 0 jest jednym z jego pierwiastków. Udowodnić, że wielomian 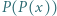 również ma dokładnie
również ma dokładnie  różnych pierwiastków całkowitych.
różnych pierwiastków całkowitych.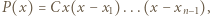 gdzie
gdzie 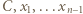 są liczbami całkowitymi. Oczywiście
są liczbami całkowitymi. Oczywiście 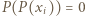 dla
dla 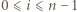 (przyjmujemy
(przyjmujemy 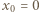 ). Załóżmy, że
). Załóżmy, że 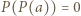 dla pewnego
dla pewnego 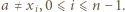 Wówczas
Wówczas 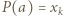 dla pewnego
dla pewnego 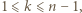 czyli
czyli 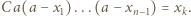 W tej sytuacji
W tej sytuacji 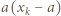 dzieli
dzieli 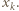 Załóżmy, że
Załóżmy, że 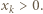 Z podzielności
Z podzielności 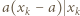 wnioskujemy kolejno
wnioskujemy kolejno 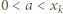 oraz
oraz 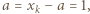 czyli
czyli 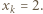 Jednak
Jednak 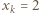 ma tylko 4 różne dzielniki całkowite, co przeczy równości
ma tylko 4 różne dzielniki całkowite, co przeczy równości 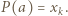 Przypadek
Przypadek 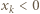 rozpatrujemy podobnie i w ten sposób kończymy dowód, że tylko pierwiastki wielomianu
rozpatrujemy podobnie i w ten sposób kończymy dowód, że tylko pierwiastki wielomianu 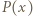 są całkowitymi pierwiastkami wielomianu
są całkowitymi pierwiastkami wielomianu 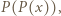 co dopełnia rozwiązanie.
co dopełnia rozwiązanie.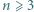 istnieją nieparzyste liczby
istnieją nieparzyste liczby 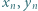 spełniające równanie
spełniające równanie 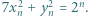
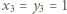 spełniają wymaganą w zadaniu równość. Załóżmy, że nieparzyste liczby
spełniają wymaganą w zadaniu równość. Załóżmy, że nieparzyste liczby 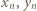 spełniają
spełniają 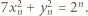 Wówczas
Wówczas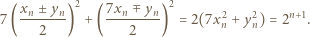
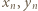 są nieparzyste, to jedna z par
są nieparzyste, to jedna z par 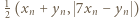 oraz
oraz 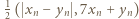 składa się z dwóch liczb nieparzystych, i tę parę wybieramy jako
składa się z dwóch liczb nieparzystych, i tę parę wybieramy jako 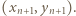 W ten indukcyjny sposób możemy skonstruować rozwiązanie wyjściowego równania dla dowolnej liczby naturalnej
W ten indukcyjny sposób możemy skonstruować rozwiązanie wyjściowego równania dla dowolnej liczby naturalnej 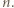

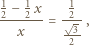
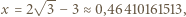 czyli stosunek pola kwadratu do pola trójkąta wynosi
czyli stosunek pola kwadratu do pola trójkąta wynosi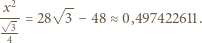
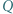 zawarty jest wielokąt o największym możliwym polu, podobny do danego wielokąta wypukłego
zawarty jest wielokąt o największym możliwym polu, podobny do danego wielokąta wypukłego 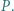 Jaką część pola
Jaką część pola 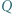 zajmuje ten wielokąt?
zajmuje ten wielokąt?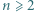 punktów czarnych i
punktów czarnych i 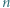 białych. Rysujemy
białych. Rysujemy 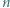 cięciw, z których każda ma jeden koniec biały a drugi czarny. Udowodnić, że można zrobić to tak, by każde dwie narysowane cięciwy przecinały się.
cięciw, z których każda ma jeden koniec biały a drugi czarny. Udowodnić, że można zrobić to tak, by każde dwie narysowane cięciwy przecinały się. cięciw "byle jak" i zastosować rozumowanie podobne do tego, które przedstawiono we wstępie.
cięciw "byle jak" i zastosować rozumowanie podobne do tego, które przedstawiono we wstępie.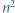 płytek w kształcie trójkąta równobocznego o boku 1 ułożono trójkąt równoboczny o boku
płytek w kształcie trójkąta równobocznego o boku 1 ułożono trójkąt równoboczny o boku 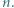 Każda płytka jest z jednej strony czerwona, a z drugiej niebieska. Ruch polega na wykonaniu następujących czynności: wybieramy płytkę
Każda płytka jest z jednej strony czerwona, a z drugiej niebieska. Ruch polega na wykonaniu następujących czynności: wybieramy płytkę 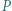 mającą wspólne boki z co najmniej dwiema płytkami, których widoczne strony mają kolor inny niż widoczna strona płytki
mającą wspólne boki z co najmniej dwiema płytkami, których widoczne strony mają kolor inny niż widoczna strona płytki 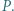 Następnie odwracamy płytkę
Następnie odwracamy płytkę 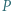 na drugą stronę. Czy ta zabawa może trwać bez końca?
na drugą stronę. Czy ta zabawa może trwać bez końca?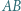 leżącej na zewnątrz tego wielokąta, przy czym cały wielokąt poza punktami
leżącej na zewnątrz tego wielokąta, przy czym cały wielokąt poza punktami 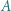 i
i 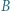 musi leżeć po jednej stronie prostej
musi leżeć po jednej stronie prostej 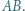 Następnie jedną z łamanych, na które punkty
Następnie jedną z łamanych, na które punkty 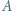 i
i 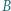 dzielą brzeg wielokąta, odbijamy środkowosymetrycznie względem środka odcinka
dzielą brzeg wielokąta, odbijamy środkowosymetrycznie względem środka odcinka 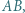 otrzymując nowy wielokąt. Dowieść, że po pewnej, skończonej liczbie takich operacji, otrzymamy wielokąt wypukły.
otrzymując nowy wielokąt. Dowieść, że po pewnej, skończonej liczbie takich operacji, otrzymamy wielokąt wypukły.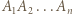 rozważmy wektory
rozważmy wektory 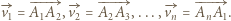 Wykonanie ruchu zmienia jedynie kolejność wektorów
Wykonanie ruchu zmienia jedynie kolejność wektorów 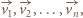 a ta jednoznacznie określa pole wielokąta.
a ta jednoznacznie określa pole wielokąta.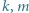 i zastępujemy je liczbami
i zastępujemy je liczbami 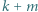 i
i 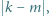 a trzecia liczba pozostaje bez zmiany. Z otrzymaną trójką postępujemy tak samo. Rozstrzygnąć, czy z każdej początkowej trójki liczb całkowitych nieujemnych można w ten sposób otrzymać trójkę, w której co najmniej dwie liczby są zerami.
a trzecia liczba pozostaje bez zmiany. Z otrzymaną trójką postępujemy tak samo. Rozstrzygnąć, czy z każdej początkowej trójki liczb całkowitych nieujemnych można w ten sposób otrzymać trójkę, w której co najmniej dwie liczby są zerami.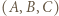 zapiszemy w postaci
zapiszemy w postaci 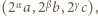 w której
w której 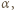
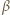 i
i 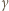 są całkowite nieujemne, zaś
są całkowite nieujemne, zaś 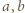 i
i  są nieparzyste lub równe
są nieparzyste lub równe 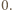 Jeśli w tej trójce jest najwyżej jedno zero, to stosując operacje z zadania, można doprowadzić do trójki
Jeśli w tej trójce jest najwyżej jedno zero, to stosując operacje z zadania, można doprowadzić do trójki 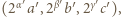 w której
w której 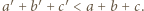 W tym celu przydatne są równości
W tym celu przydatne są równości 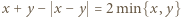 i
i 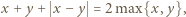 dzięki którym z trójki
dzięki którym z trójki 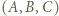 otrzymamy trójkę
otrzymamy trójkę 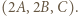
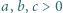 spełniają warunek
spełniają warunek 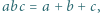 to
to 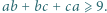
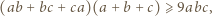
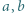 i
i  spełniają równość
spełniają równość 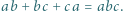 Dowieść, że
Dowieść, że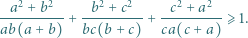
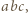 a prawą przez
a prawą przez 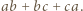 Następnie skorzystać z nierówności
Następnie skorzystać z nierówności