Składanie inwersji z symetrią»Zadanie 5
o zadaniu...
- Zadanie pochodzi z artykułu Składanie inwersji z symetrią
- Publikacja w Delcie: kwiecień 2020
- Publikacja elektroniczna: 1 kwietnia 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (390 KB)
Okrąg 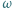 wpisany w trójkąt
wpisany w trójkąt 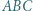 jest styczny do boku
jest styczny do boku 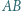 w punkcie
w punkcie 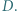 Okrąg
Okrąg 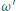 jest styczny do półprostych
jest styczny do półprostych 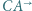 i
i 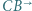 oraz jest styczny zewnętrznie w punkcie
oraz jest styczny zewnętrznie w punkcie 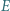 do okręgu opisanego na trójkącie
do okręgu opisanego na trójkącie 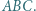 Wykazać, że
Wykazać, że 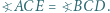
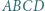 o podstawach
o podstawach 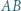 i
i 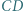 jest wpisany w okrąg
jest wpisany w okrąg 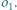 Okrąg
Okrąg 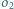 jest styczny do odcinków
jest styczny do odcinków 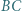 i
i 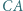 oraz jest styczny wewnętrznie do okręgu
oraz jest styczny wewnętrznie do okręgu 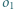 w punkcie
w punkcie 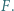 Okrąg wpisany w trójkąt
Okrąg wpisany w trójkąt 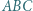 jest styczny do odcinka
jest styczny do odcinka 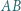 w punkcie
w punkcie 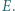 Dowieść, że punkty
Dowieść, że punkty 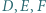 leżą na jednej prostej.
leżą na jednej prostej.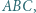 w którym
w którym 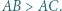 Punkty
Punkty 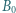 i
i 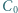 są odpowiednio środkami boków
są odpowiednio środkami boków 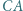 i
i 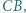 a punkt
a punkt 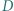 jest spodkiem wysokości opuszczonej z wierzchołka
jest spodkiem wysokości opuszczonej z wierzchołka 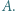 Okrąg przechodzący przez punkty
Okrąg przechodzący przez punkty 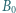 i
i 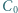 jest styczny do okręgu opisanego na trójkącie
jest styczny do okręgu opisanego na trójkącie 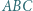 w punkcie
w punkcie 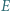 różnym od
różnym od 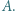 Udowodnić, że środek ciężkości trójkąta
Udowodnić, że środek ciężkości trójkąta 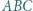 leży na prostej
leży na prostej 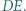
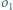 jest styczny do boków
jest styczny do boków 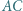 i
i 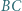 trójkąta
trójkąta 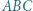 oraz do okręgu opisanego na tym trójkącie w punkcie
oraz do okręgu opisanego na tym trójkącie w punkcie 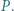 Okrąg
Okrąg 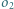 jest styczny do półprostych
jest styczny do półprostych 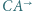 i
i 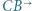 oraz jest styczny zewnętrznie do okręgu opisanego na trójkącie
oraz jest styczny zewnętrznie do okręgu opisanego na trójkącie 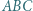 w punkcie
w punkcie 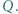 Wykazać, że
Wykazać, że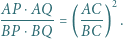
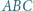 jest wpisany w okrąg
jest wpisany w okrąg 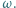 Prosta
Prosta 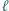 jest równoległa do prostej
jest równoległa do prostej 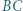 i przecina odcinki
i przecina odcinki 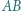 i
i 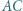 odpowiednio w punktach
odpowiednio w punktach 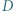 i
i 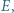 a okrąg
a okrąg 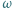 w punktach
w punktach 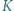 i
i 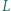 (gdzie
(gdzie 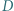 leży między punktami
leży między punktami 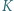 i
i 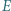 ). Okrąg
). Okrąg 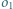 jest styczny do odcinków
jest styczny do odcinków 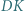 i
i 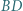 oraz do okręgu
oraz do okręgu  ; okrąg
; okrąg 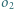 jest styczny do odcinków
jest styczny do odcinków 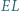 i
i 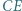 oraz do okręgu
oraz do okręgu  Wyznaczyć miejsce geometryczne punktów przecięcia wspólnych stycznych wewnętrznych okręgów
Wyznaczyć miejsce geometryczne punktów przecięcia wspólnych stycznych wewnętrznych okręgów 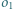 i
i 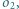 przy zmieniającym się położeniu prostej
przy zmieniającym się położeniu prostej 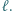
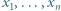 należą do odcinka
należą do odcinka ![[0,1].](/math/temat/matematyka/analiza/zadania/2020/02/29/zm-1632/2x-a703a273548e97ab80323cc80e76f4c2e0b71aa8-im-2C,6B,73-FF,FF,FF.gif) Udowodnić, że istnieje takie
Udowodnić, że istnieje takie 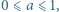 że
że 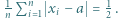
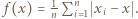 Ponieważ
Ponieważ 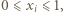 więc
więc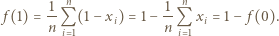
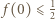 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 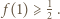 Teza wynika zatem z ciągłości funkcji
Teza wynika zatem z ciągłości funkcji 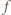 i własności Darboux funkcji ciągłych.
i własności Darboux funkcji ciągłych.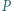 leży wewnątrz trójkąta ostrokątnego
leży wewnątrz trójkąta ostrokątnego 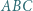 i nie jest środkiem okręgu
i nie jest środkiem okręgu 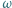 opisanego na tym trójkącie. Udowodnić, że wśród odcinków
opisanego na tym trójkącie. Udowodnić, że wśród odcinków 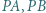 i
i 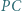 znajdują się odcinek krótszy oraz odcinek dłuższy od promienia okręgu
znajdują się odcinek krótszy oraz odcinek dłuższy od promienia okręgu 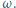
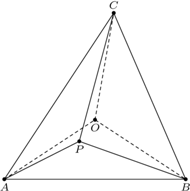
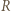 leży wewnątrz trójkąta
leży wewnątrz trójkąta 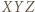 i
i 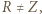 to
to 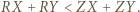 Aby go udowodnić, zauważmy najpierw, że
Aby go udowodnić, zauważmy najpierw, że 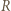 nie leży na co najmniej jednym z odcinków
nie leży na co najmniej jednym z odcinków 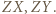 Bez straty ogólności przyjmijmy, że jest to
Bez straty ogólności przyjmijmy, że jest to 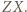 Niech
Niech 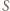 będzie punktem przecięcia prostych
będzie punktem przecięcia prostych 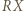 i
i 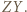 Wtedy z nierówności trójkąta:
Wtedy z nierówności trójkąta: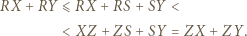
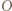 będzie środkiem okręgu
będzie środkiem okręgu 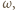 a
a  będzie promieniem tego okręgu. Punkt
będzie promieniem tego okręgu. Punkt 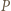 leży w co najmniej jednym z trójkątów
leży w co najmniej jednym z trójkątów 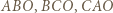 ; bez straty ogólności przyjmijmy, że jest to trójkąt
; bez straty ogólności przyjmijmy, że jest to trójkąt 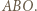 Podobnie,
Podobnie, 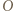 leży w którymś z trójkątów
leży w którymś z trójkątów 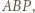
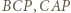 ; przyjmijmy, że jest to trójkąt
; przyjmijmy, że jest to trójkąt 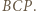 Zgodnie z lematem zachodzi
Zgodnie z lematem zachodzi 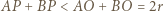 ; i analogicznie:
; i analogicznie: 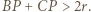 Zatem któryś z odcinków
Zatem któryś z odcinków 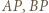 jest mniejszy od
jest mniejszy od  i któryś z odcinków
i któryś z odcinków 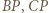 jest większy od
jest większy od 
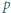 będzie liczbą pierwszą większą od 2. Udowodnić, że istnieje dokładnie jeden sposób przedstawienia
będzie liczbą pierwszą większą od 2. Udowodnić, że istnieje dokładnie jeden sposób przedstawienia 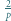 w postaci sumy
w postaci sumy 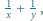 gdzie
gdzie 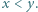
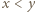 spełniają
spełniają 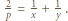 Równanie to można sprowadzić do postaci
Równanie to można sprowadzić do postaci 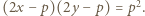 Ponieważ
Ponieważ 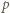 jest liczbą pierwszą, wynika stąd, że
jest liczbą pierwszą, wynika stąd, że 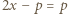 lub
lub 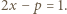 Pierwsza z tych możliwości oznaczałaby, że
Pierwsza z tych możliwości oznaczałaby, że 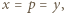 co przeczy zależności
co przeczy zależności 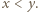 Musi być zatem
Musi być zatem 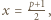 skąd
skąd 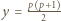 ; ponieważ
; ponieważ 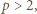 liczby te są całkowite i faktycznie spełniają wymaganą równość.
liczby te są całkowite i faktycznie spełniają wymaganą równość.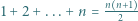 i
i 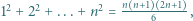 wyprowadzić wzór na
wyprowadzić wzór na 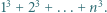
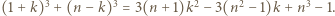
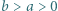 zachodzi nierówność
zachodzi nierówność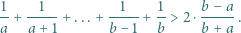
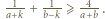
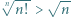 dla naturalnych
dla naturalnych 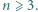
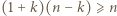 dla
dla 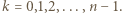 Ponadto dla
Ponadto dla 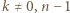 nierówność jest ostra.
nierówność jest ostra. zachodzą następujące równości:
zachodzą następujące równości: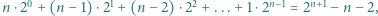
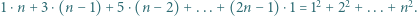
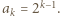
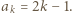 Przyda się też równość
Przyda się też równość 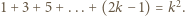
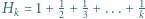 dla całkowitych dodatnich
dla całkowitych dodatnich 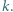 Udowodnić, że
Udowodnić, że 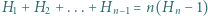 dla naturalnych
dla naturalnych 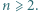
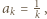 gdzie
gdzie 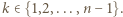
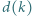 oznacza liczbę dzielników liczby naturalnej
oznacza liczbę dzielników liczby naturalnej 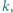 zaś
zaś 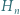 - jak w poprzednim zadaniu. Dowieść, że
- jak w poprzednim zadaniu. Dowieść, że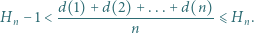
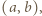 dla których
dla których 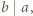 gdzie
gdzie 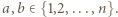 Po sporządzeniu tabeli w kolumnach mamy kolejno
Po sporządzeniu tabeli w kolumnach mamy kolejno 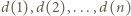 par, a w wierszach
par, a w wierszach 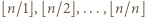 par. Trzeba jeszcze zastosować nierówność
par. Trzeba jeszcze zastosować nierówność 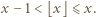
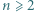 zachodzi równość
zachodzi równość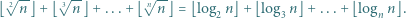
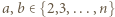 zaznaczamy takie pola
zaznaczamy takie pola 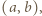 dla których
dla których 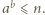 Wówczas w
Wówczas w 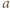 -tej kolumnie mamy
-tej kolumnie mamy 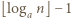 zaznaczonych pól, zaś w
zaznaczonych pól, zaś w 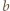 -tym wierszu jest ich
-tym wierszu jest ich 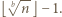
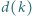 będzie jak w zadaniu 6. Ustalmy liczbę rzeczywistą
będzie jak w zadaniu 6. Ustalmy liczbę rzeczywistą 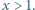 Dowieść, że dla wszystkich naturalnych
Dowieść, że dla wszystkich naturalnych 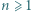 zachodzi nierówność
zachodzi nierówność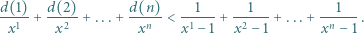
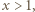 mamy
mamy 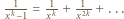 Dla
Dla 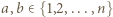 w polu
w polu 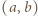 tabeli umieszczamy liczbę
tabeli umieszczamy liczbę 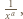 jeśli
jeśli 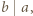 w przeciwnym razie umieszczamy 0. Sumując kolumnami, otrzymamy lewą stronę dowodzonej nierówności, natomiast wierszami - liczbę mniejszą od prawej strony.
w przeciwnym razie umieszczamy 0. Sumując kolumnami, otrzymamy lewą stronę dowodzonej nierówności, natomiast wierszami - liczbę mniejszą od prawej strony.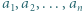 spełniają równości
spełniają równości 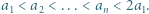 Udowodnić, że jeśli
Udowodnić, że jeśli 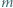 jest liczbą różnych dzielników pierwszych iloczynu
jest liczbą różnych dzielników pierwszych iloczynu 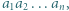 to
to 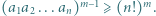
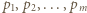 będą różnymi dzielnikami pierwszymi iloczynu
będą różnymi dzielnikami pierwszymi iloczynu 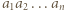 oraz niech
oraz niech 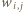 oznacza wykładnik liczby
oznacza wykładnik liczby 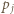 w rozkładzie
w rozkładzie 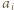 na czynniki pierwsze dla
na czynniki pierwsze dla 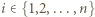 i
i 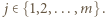 W pole tabeli o współrzędnych
W pole tabeli o współrzędnych 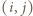 wpisujemy
wpisujemy 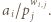 Należy zaobserwować, że w każdym wierszu są różne liczby całkowite dodatnie, więc ich iloczyn wynosi co najmniej
Należy zaobserwować, że w każdym wierszu są różne liczby całkowite dodatnie, więc ich iloczyn wynosi co najmniej 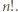 Ponadto iloczyny liczb w kolejnych kolumnach są równe
Ponadto iloczyny liczb w kolejnych kolumnach są równe 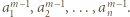
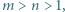 przy czym
przy czym 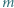 jest liczbą parzystą. Udowodnić, że równanie
jest liczbą parzystą. Udowodnić, że równanie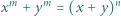
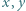 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 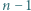 dzieli się przez
dzieli się przez 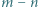 .
.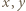 spełniają podane równanie. Oznaczmy przez
spełniają podane równanie. Oznaczmy przez 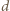 ich największy wspólny dzielnik; tak więc
ich największy wspólny dzielnik; tak więc 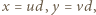 gdzie
gdzie 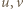 to liczby naturalne względnie pierwsze. Wstawiając to do równania i dzieląc stronami przez
to liczby naturalne względnie pierwsze. Wstawiając to do równania i dzieląc stronami przez 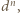 otrzymujemy
otrzymujemy
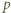 będzie dowolnym dzielnikiem pierwszym liczby
będzie dowolnym dzielnikiem pierwszym liczby 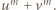 Wobec związku (1)
Wobec związku (1) 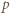 jest też dzielnikiem sumy
jest też dzielnikiem sumy 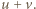 To znaczy, że
To znaczy, że 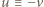 (mod
(mod 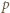 ); a skoro
); a skoro 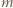 jest liczbą parzystą, mamy stąd
jest liczbą parzystą, mamy stąd 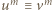 (mod
(mod 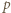 ), i dalej
), i dalej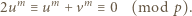
 nie dzieli się przez
nie dzieli się przez 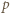 (bo
(bo 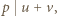 zaś
zaś 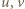 są względnie pierwsze); zatem
są względnie pierwsze); zatem 
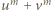 nie ma innych dzielników pierwszych, znaczy to, że
nie ma innych dzielników pierwszych, znaczy to, że
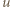 i
i  (względnie pierwsze) są obie nieparzyste; stąd
(względnie pierwsze) są obie nieparzyste; stąd 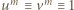 (mod 4), bo
(mod 4), bo 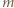 jest liczbą parzystą. W równości (2) mamy więc
jest liczbą parzystą. W równości (2) mamy więc 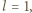 skąd
skąd 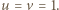 Wracamy do równania (1):
Wracamy do równania (1): 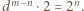 To pokazuje, że
To pokazuje, że 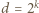 (dla pewnego
(dla pewnego 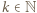 ); przy tym
); przy tym 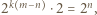 czyli
czyli 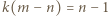 : liczba
: liczba 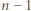 dzieli się przez
dzieli się przez 
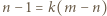 dla pewnego
dla pewnego 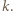 Wówczas para
Wówczas para 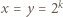 jest rozwiązaniem zadanego równania:
jest rozwiązaniem zadanego równania: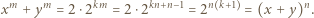
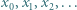 jest określony rekurencyjnie:
jest określony rekurencyjnie: 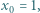
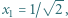
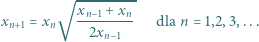
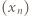 wynika (przez oczywistą indukcję), że wszystkie jego wyrazy są dobrze określonymi liczbami dodatnimi. Weźmy pod uwagę ilorazy
wynika (przez oczywistą indukcję), że wszystkie jego wyrazy są dobrze określonymi liczbami dodatnimi. Weźmy pod uwagę ilorazy 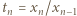 ; ciąg liczb dodatnich
; ciąg liczb dodatnich 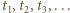 z wyrazem początkowym
z wyrazem początkowym 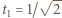 spełnia zależność rekurencyjną
spełnia zależność rekurencyjną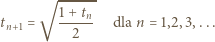
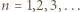 zachodzi równość
zachodzi równość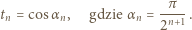
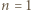 tak jest. Przyjmijmy równość
tak jest. Przyjmijmy równość 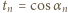 dla pewnego
dla pewnego 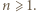 Ponieważ
Ponieważ 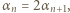 mamy wówczas
mamy wówczas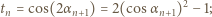
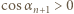 ):
):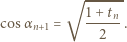
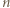 zastąpionym przez
zastąpionym przez 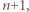 czyli tezę indukcyjną.
czyli tezę indukcyjną.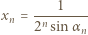
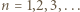 Znów indukcja: dla
Znów indukcja: dla 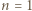 zgadza się (bo
zgadza się (bo 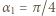 ). Ustalmy
). Ustalmy 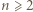 i przyjmijmy słuszność (3) z
i przyjmijmy słuszność (3) z 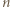 zastąpionym przez
zastąpionym przez 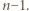 Z takiego założenia indukcyjnego i ze wzoru (2) otrzymujemy
Z takiego założenia indukcyjnego i ze wzoru (2) otrzymujemy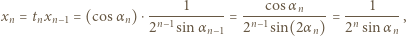
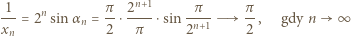
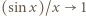 przy
przy 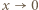 ). Stąd, ostatecznie,
). Stąd, ostatecznie, 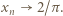
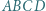 zachodzi równość
zachodzi równość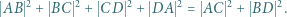
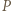 będzie punktem przecięcia przekątnych równoległoboku. Wyznaczyć
będzie punktem przecięcia przekątnych równoległoboku. Wyznaczyć 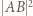 z twierdzenia cosinusów dla trójkąta
z twierdzenia cosinusów dla trójkąta 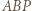 , podobnie trzy pozostałe kwadraty długości boków.
, podobnie trzy pozostałe kwadraty długości boków.