Zadanie ZM-1552
o zadaniu...
- Publikacja w Delcie: styczeń 2018
- Publikacja elektroniczna: 1 stycznia 2018
Wykazać, że istnieje nieskończenie wiele par liczb całkowitych dodatnich 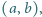 dla których liczba
dla których liczba

jest kwadratem liczby całkowitej.
Wykazać, że istnieje nieskończenie wiele par liczb całkowitych dodatnich 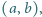 dla których liczba
dla których liczba

jest kwadratem liczby całkowitej.
Zadanie 754 zaproponował pan Mikołaj Pater.
Znaleźć wszystkie trójki liczb rzeczywistych 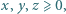 spełniające układ równań
spełniające układ równań
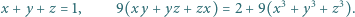
Wewnątrz trójkąta 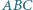 leży punkt
leży punkt 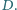 Proste
Proste 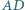 i
i 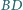 przecinają boki
przecinają boki 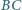 i
i 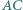 odpowiednio w punktach
odpowiednio w punktach 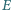 i
i 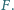 Udowodnić, że jeśli
Udowodnić, że jeśli 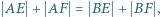 to
to 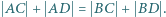
Na okrągłym stoliku gracze kładą złotówki, przy czym nie mogą one wystawać poza stolik ani nachodzić na siebie oraz nie wolno przesuwać leżących już monet.
Gracze rysują takie przekątne 12-kąta foremnego, które się nie przecinają.
Na płaszczyźnie danych jest 20 wektorów. Gracze wybierają po jednym z nich. Wygrywa ten, kto na końcu ma dłuższą sumę wybranych wektorów.
Gracze stawiają pionki, po jednym, na polach nieskończonej szachownicy. Gracz wygrywa, jeżeli utworzy ze swoich pionków kwadrat 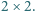
Planszą do gry są wierzchołki trójkąta oraz 7 punktów z jego wnętrza, żadne trzy punkty planszy nie są współliniowe. Gracze rysują nieprzecinające się odcinki łączące dwa z danych 10 punktów.
Dana jest tablica  Dwaj gracze na przemian wykonują ruchy, z których każdy polega na wybraniu białego albo czarnego pionka i postawieniu go na wybranym wolnym polu. Wygrywa ten, którego ruch doprowadził do powstania ciągu 5 kolejnych pionków tego samego koloru w linii pionowej, poziomej lub ukośnej. Zbadaj, czy dla gracza rozpoczynającego grę istnieje strategia zapewniająca mu zwycięstwo.
Dwaj gracze na przemian wykonują ruchy, z których każdy polega na wybraniu białego albo czarnego pionka i postawieniu go na wybranym wolnym polu. Wygrywa ten, którego ruch doprowadził do powstania ciągu 5 kolejnych pionków tego samego koloru w linii pionowej, poziomej lub ukośnej. Zbadaj, czy dla gracza rozpoczynającego grę istnieje strategia zapewniająca mu zwycięstwo.
Wykazać, że każdą dodatnią liczbę całkowitą można zapisać w postaci różnicy dwóch dodatnich liczb całkowitych, które mają tę samą liczbę różnych dzielników pierwszych.
Dodatnie liczby rzeczywiste 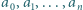 są takie, że
są takie, że 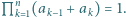 Udowodnić, że
Udowodnić, że
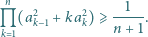
Dany jest okrąg 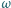 o średnicy
o średnicy 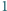 oraz łamana
oraz łamana  o końcach należących do tego okręgu, której długość jest mniejsza od
o końcach należących do tego okręgu, której długość jest mniejsza od  Udowodnić, że istnieje średnica okręgu
Udowodnić, że istnieje średnica okręgu 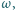 która jest rozłączna z
która jest rozłączna z 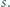
Zadanie 752 zaproponował pan Witold Bednarek z Łodzi.
Znaleźć wszystkie pary liczb całkowitych dodatnich, których średnia arytmetyczna i średnia geometryczna różnią się o 1.
Trójkąt równoboczny o boku długości 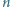 został podzielony (prostymi równoległymi do boków) na
został podzielony (prostymi równoległymi do boków) na 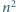 trójkątów o boku 1 (trójkątów jednostkowych). Wierzchołkom powstałej siatki zostały przyporządkowane różne liczby rzeczywiste (
trójkątów o boku 1 (trójkątów jednostkowych). Wierzchołkom powstałej siatki zostały przyporządkowane różne liczby rzeczywiste ( 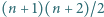 różnych liczb). Trójkąt jednostkowy nazwiemy zorientowanym dodatnio, jeśli - idąc wzdłuż jego brzegu, w kierunku wzrastania liczb przy wierzchołkach (tj. startując od najmniejszej i idąc przez średnią do największej) - mamy jego wnętrze po lewej stronie. Dla ustalonej liczby naturalnej
różnych liczb). Trójkąt jednostkowy nazwiemy zorientowanym dodatnio, jeśli - idąc wzdłuż jego brzegu, w kierunku wzrastania liczb przy wierzchołkach (tj. startując od najmniejszej i idąc przez średnią do największej) - mamy jego wnętrze po lewej stronie. Dla ustalonej liczby naturalnej  wyznaczyć najmniejszą i największą możliwą wartość liczby trójkątów jednostkowych zorientowanych dodatnio.
wyznaczyć najmniejszą i największą możliwą wartość liczby trójkątów jednostkowych zorientowanych dodatnio.
Ciąg liczb całkowitych 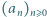 definiujemy rekurencyjnie:
definiujemy rekurencyjnie: 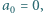
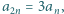
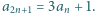 Scharakteryzuj wszystkie liczby całkowite
Scharakteryzuj wszystkie liczby całkowite 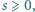 dla których istnieje dokładnie jedna para
dla których istnieje dokładnie jedna para 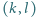 spełniająca warunki
spełniająca warunki 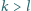 oraz
oraz 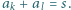
Oblicz 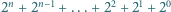 oraz
oraz 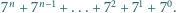
Rozważmy ciąg 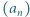 zadany przez
zadany przez 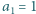 oraz
oraz 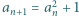 dla
dla 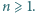 Rozstrzygnąć, czy istnieje dodatnia liczba całkowita
Rozstrzygnąć, czy istnieje dodatnia liczba całkowita 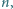 dla której
dla której
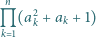
jest kwadratem liczby całkowitej.
Zadanie 750 zaproponował pan Tomasz Ordowski.
Znaleźć wszystkie pary liczb pierwszych 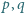
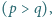 dla których także liczby
dla których także liczby 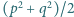 oraz
oraz 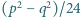 są pierwsze.
są pierwsze.
Trójkąt 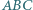 jest opisany na okręgu o środku
jest opisany na okręgu o środku 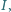 stycznym do boków
stycznym do boków 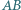 i
i 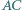 w punktach
w punktach 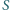 i
i 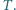 Na boku
Na boku 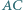 leży taki punkt
leży taki punkt 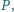 że
że 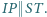 Proste
Proste 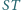 i
i 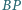 przecinają się w punkcie
przecinają się w punkcie 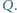 Dowieść, że
Dowieść, że