Klub 44M - zadania XII 2012»Zadanie 652
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania XII 2012
- Publikacja w Delcie: grudzień 2012
- Publikacja elektroniczna: 30 listopada 2012
- Artykuł źródłowy w wersji do druku [application/pdf]: (74 KB)
Zadanie 652 zaproponował pan Witold Bednarek z Łodzi.
Udowodnić nierówność
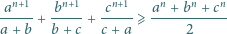
dla liczb rzeczywistych
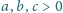 oraz liczb całkowitych
oraz liczb całkowitych
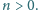
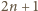 liczb, mianowicie
liczb, mianowicie
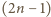 -krotnie powtórzonej liczby
-krotnie powtórzonej liczby
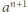 oraz liczb
oraz liczb
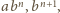 jest nie mniejsza od ich średniej geometrycznej, równej
jest nie mniejsza od ich średniej geometrycznej, równej
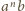 :
:
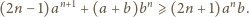
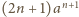 i po prostym przekształceniu
otrzymujemy
i po prostym przekształceniu
otrzymujemy
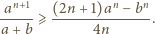
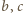 oraz
oraz
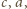 po czym dodać te trzy nierówności, by uzyskać tezę
zadania.
po czym dodać te trzy nierówności, by uzyskać tezę
zadania.
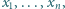 które są nie mniejsze niż
które są nie mniejsze niż
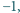 spełniają
równość
spełniają
równość
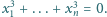 Udowodnić, że
Udowodnić, że
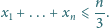
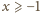 zachodzi
zachodzi
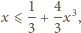
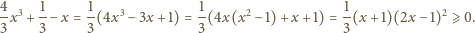
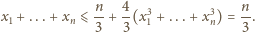
 o podstawach
o podstawach
 i
i
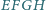 będących kwadratami, przy czym
będących kwadratami, przy czym
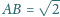 i
i
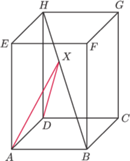
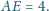 Punkt
Punkt
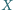 przesuwamy po przekątnej
przesuwamy po przekątnej
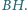 Znaleźć
minimalną wartość wyrażenia
Znaleźć
minimalną wartość wyrażenia
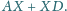
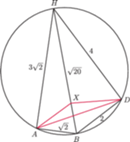
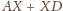 wynosi
wynosi
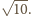
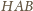 i
i
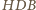 na jednej
płaszczyźnie, dostajemy czworokąt
na jednej
płaszczyźnie, dostajemy czworokąt
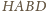 wpisany w okrąg.
wpisany w okrąg.
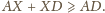 Równość zachodzi wtedy i tylko
wtedy, gdy
Równość zachodzi wtedy i tylko
wtedy, gdy
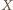 jest punktem przecięcia przekątnych tego czworokąta.
Szukana minimalna wartość wyrażenia
jest punktem przecięcia przekątnych tego czworokąta.
Szukana minimalna wartość wyrażenia
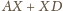 to długość
odcinka
to długość
odcinka
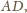 którą możemy obliczyć z twierdzenia Ptolemeusza:
którą możemy obliczyć z twierdzenia Ptolemeusza:
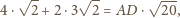
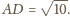
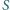 o środku w środku okręgu opisanego na trójkącie
o środku w środku okręgu opisanego na trójkącie
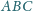 przecina krawędzie
przecina krawędzie
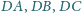 czworościanu
czworościanu
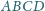 odpowiednio w punktach
odpowiednio w punktach
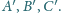 Płaszczyzny styczne
do tej sfery odpowiednio w punktach
Płaszczyzny styczne
do tej sfery odpowiednio w punktach
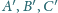 przecinają się w punkcie
przecinają się w punkcie
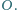 Wykazać, że punkt
Wykazać, że punkt
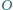 jest środkiem sfery opisanej na
czworościanie
jest środkiem sfery opisanej na
czworościanie
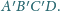
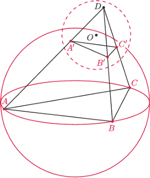
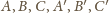 i sfera
opisana na czworościanie
i sfera
opisana na czworościanie
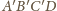 są prostopadłe. Zauważmy,
że
są prostopadłe. Zauważmy,
że
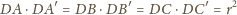
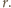 Rozważmy inwersję o środku
Rozważmy inwersję o środku
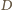 i promieniu
i promieniu
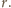 Zauważmy, że sfera
Zauważmy, że sfera
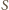 przechodzi na siebie, a punkty
przechodzi na siebie, a punkty
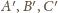 odpowiednio na
odpowiednio na
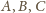 (i na odwrót). Obrazem
drugiej z rozważanych sfer będzie więc płaszczyzna przechodząca przez
punkty
(i na odwrót). Obrazem
drugiej z rozważanych sfer będzie więc płaszczyzna przechodząca przez
punkty
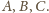 Jednakże środek sfery
Jednakże środek sfery
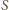 leży właśnie na
płaszczyźnie
leży właśnie na
płaszczyźnie
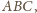 skąd wniosek, że płaszczyzna ta jest do niej
prostopadła. A skoro inwersja zachowuje kąty między powierzchniami, to sfera
przechodząca przez punkty
skąd wniosek, że płaszczyzna ta jest do niej
prostopadła. A skoro inwersja zachowuje kąty między powierzchniami, to sfera
przechodząca przez punkty
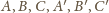 i sfera opisana na
czworościanie
i sfera opisana na
czworościanie
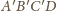 też są prostopadłe.
też są prostopadłe.
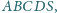 którego podstawą jest czworokąt wypukły
którego podstawą jest czworokąt wypukły
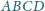 o prostopadłych przekątnych
o prostopadłych przekątnych
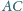 i
i
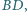 a rzutem
prostokątnym wierzchołka
a rzutem
prostokątnym wierzchołka
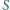 na podstawę jest punkt
na podstawę jest punkt
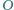 przecięcia
przekątnych podstawy. Udowodnić, że rzuty prostokątne punktu
przecięcia
przekątnych podstawy. Udowodnić, że rzuty prostokątne punktu
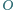 na
ściany boczne ostrosłupa leżą na jednym okręgu.
na
ściany boczne ostrosłupa leżą na jednym okręgu.
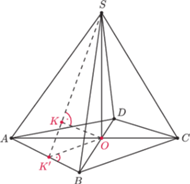
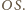 Weźmy rzut stereograficzny tej sfery z punktu
Weźmy rzut stereograficzny tej sfery z punktu
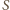 na
płaszczyznę
na
płaszczyznę
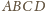 (
(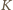 będzie rzutem prostokątnym
punktu
będzie rzutem prostokątnym
punktu
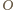 na ścianę
na ścianę
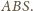 Płaszczyzna
Płaszczyzna
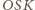 jest
prostopadła do krawędzi
jest
prostopadła do krawędzi
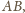 skąd wynika, że obraz
skąd wynika, że obraz
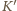 punktu
punktu
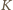 w tym przekształceniu będzie rzutem prostokątnym punktu
w tym przekształceniu będzie rzutem prostokątnym punktu
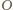 na krawędź
na krawędź
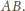 Analogicznie udowodnimy, że obrazami
pozostałych rzutów są rzuty punktu
Analogicznie udowodnimy, że obrazami
pozostałych rzutów są rzuty punktu
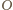 na pozostałe boki czworokąta
na pozostałe boki czworokąta
 Jednakże w czworokącie o prostopadłych przekątnych rzuty
prostokątne punktu przecięcia przekątnych leżą na jednym okręgu (łatwy
dowód tego faktu pozostawiamy Czytelnikowi –
Jednakże w czworokącie o prostopadłych przekątnych rzuty
prostokątne punktu przecięcia przekątnych leżą na jednym okręgu (łatwy
dowód tego faktu pozostawiamy Czytelnikowi – 
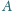 czworościanu
czworościanu
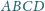 poprowadzono
płaszczyznę styczną do sfery opisanej na tym czworościanie. Udowodnić, że
proste, wzdłuż których płaszczyzna ta przecina płaszczyzny ścian
poprowadzono
płaszczyznę styczną do sfery opisanej na tym czworościanie. Udowodnić, że
proste, wzdłuż których płaszczyzna ta przecina płaszczyzny ścian
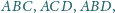 tworzą sześć równych kątów wtedy i tylko wtedy,
gdy
tworzą sześć równych kątów wtedy i tylko wtedy,
gdy

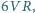 gdzie
gdzie
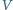 i
i
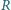 oznaczają odpowiednio objętość i promień sfery
opisanej na czworościanie (wzór Crellego).
oznaczają odpowiednio objętość i promień sfery
opisanej na czworościanie (wzór Crellego).

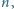 dla których kwadrat
złożony z
dla których kwadrat
złożony z
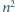 kwadracików jednostkowych można pokryć
płytkami powstałymi z płytki pokazanej na rysunku przez obrót o kąt
kwadracików jednostkowych można pokryć
płytkami powstałymi z płytki pokazanej na rysunku przez obrót o kąt
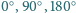 lub
lub
 w ten sposób, by płytki nie zachodziły na
siebie.
w ten sposób, by płytki nie zachodziły na
siebie.

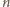 jest
podzielne przez
jest
podzielne przez
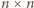 udało się
pokryć dostępnymi płytkami. Skoro pole płytki wynosi
udało się
pokryć dostępnymi płytkami. Skoro pole płytki wynosi
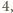 to
to
 musi być parzyste, powiedzmy
musi być parzyste, powiedzmy
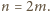 Rozważmy
kolorowanie naszego kwadratu jak standardowej szachownicy i zauważmy, że
każda płytka jest jednego z dwóch rodzajów: zawiera
Rozważmy
kolorowanie naszego kwadratu jak standardowej szachownicy i zauważmy, że
każda płytka jest jednego z dwóch rodzajów: zawiera
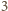 czarne pola
lub
czarne pola
lub
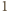 czarne pole. Niech liczba płytek pierwszego rodzaju wynosi
czarne pole. Niech liczba płytek pierwszego rodzaju wynosi
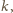 a drugiego
a drugiego
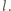 Zliczając czarne i białe pola, otrzymujemy
Zliczając czarne i białe pola, otrzymujemy
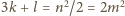 oraz
oraz
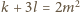 (dzięki temu, że
(dzięki temu, że
 jest parzyste, mamy po równo pól czarnych i białych!). Stąd
w szczególności
jest parzyste, mamy po równo pól czarnych i białych!). Stąd
w szczególności
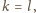 więc
więc
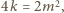 zatem
zatem
 jest
parzyste, a
jest
parzyste, a
 – podzielne przez
– podzielne przez
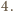
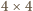 spełniające
warunki zadania, więc także dowolnego kwadratu
spełniające
warunki zadania, więc także dowolnego kwadratu
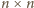 dla
dla
 będącego wielokrotnością
będącego wielokrotnością
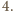
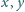 spełniają równość
spełniają równość
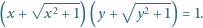
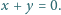
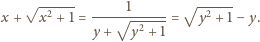
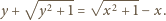
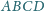 kąt
kąt
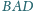 jest prosty. Wykaż, że
jest prosty. Wykaż, że

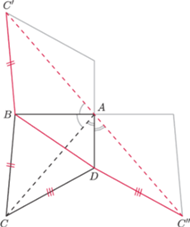
 symetrycznie względem prostych
symetrycznie względem prostych
 oraz
oraz
 i przyjmijmy oznaczenia jak na rysunku.
Wówczas
i przyjmijmy oznaczenia jak na rysunku.
Wówczas
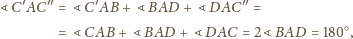
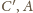 i
i
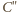 leżą, w tej właśnie kolejności, na
jednej prostej. Ponadto
leżą, w tej właśnie kolejności, na
jednej prostej. Ponadto
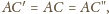 stąd
stąd
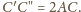
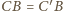 oraz
oraz
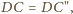 zatem
zatem
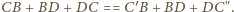 Teza wynika z faktu, że łamana
Teza wynika z faktu, że łamana
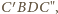 łącząca punkty
łącząca punkty
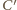 i
i
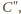 nie może być krótsza
niż odcinek
nie może być krótsza
niż odcinek
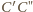 pomiędzy nimi:
pomiędzy nimi:
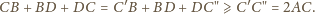
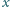 istnieją takie liczby niewymierne
istnieją takie liczby niewymierne
 i
i
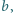 że
że
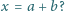
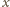 można wskazać odpowiednie liczby
można wskazać odpowiednie liczby
 i
i
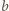 w następujący sposób.
w następujący sposób.
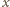 jest niewymierna, to niewymierne są także liczby
jest niewymierna, to niewymierne są także liczby
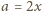 oraz
oraz
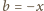 (dlaczego?). Wówczas, oczywiście,
(dlaczego?). Wówczas, oczywiście,
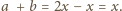
 jest wymierna, to liczba
jest wymierna, to liczba
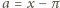 jest
niewymierna (dlaczego?). Wówczas, przyjmując
jest
niewymierna (dlaczego?). Wówczas, przyjmując
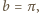 mamy
mamy
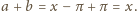
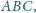 wpisane w ustalony
okrąg
wpisane w ustalony
okrąg
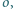 spełniające następujący warunek: środek ciężkości
spełniające następujący warunek: środek ciężkości
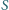 trójkąta
trójkąta
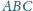 pokrywa się z ortocentrum
pokrywa się z ortocentrum
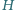 trójkąta
trójkąta
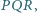 gdzie
gdzie
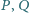 i
i
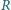 to odpowiednio punkty przecięcia
półprostych
to odpowiednio punkty przecięcia
półprostych
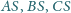 z okręgiem
z okręgiem
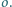

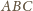 musi być równoboczny.
musi być równoboczny.
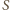 jest ortocentrum trójkąta
jest ortocentrum trójkąta
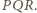 Mamy
równość kątów
Mamy
równość kątów
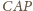 i
i
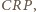 jako wpisanych opartych na tym
samym łuku. Skoro jednak
jako wpisanych opartych na tym
samym łuku. Skoro jednak
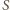 jest ortocentrum, to kąt
jest ortocentrum, to kąt
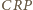 jest
równy kątowi
jest
równy kątowi
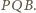 Ten z kolei jest oparty na tym samym łuku co kąt
Ten z kolei jest oparty na tym samym łuku co kąt
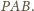 Zatem
Zatem
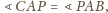 czyli
czyli
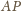 jest dwusieczną
i zarazem środkową w trójkącie
jest dwusieczną
i zarazem środkową w trójkącie
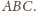 Zatem
Zatem
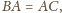 co
wynika np. z twierdzenia o dwusiecznej. Analogicznie dowodzimy, że
co
wynika np. z twierdzenia o dwusiecznej. Analogicznie dowodzimy, że
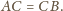
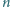 będzie liczbą pięciocyfrową w zapisie dziesiętnym (pierwsza
cyfra jest różna od
będzie liczbą pięciocyfrową w zapisie dziesiętnym (pierwsza
cyfra jest różna od
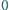 ) i niech
) i niech
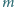 będzie liczbą czterocyfrową
powstałą z
będzie liczbą czterocyfrową
powstałą z
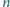 przez wyrzucenie jej środkowej cyfry. Znaleźć wszystkie
takie liczby
przez wyrzucenie jej środkowej cyfry. Znaleźć wszystkie
takie liczby
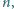 że liczba
że liczba
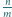 jest całkowita.
jest całkowita.
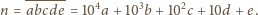
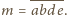 Załóżmy, że
Załóżmy, że
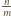 jest liczbą całkowitą.
Gdyby było
jest liczbą całkowitą.
Gdyby było
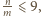 to przyjmując oznaczenia
to przyjmując oznaczenia
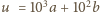 oraz
oraz
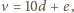 mielibyśmy
mielibyśmy
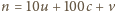 i
i
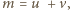 a stąd
sprzeczność:
a stąd
sprzeczność:
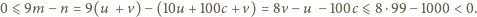
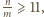 to
to
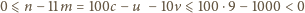
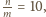 co daje
co daje
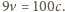 Stąd,
gdyby
Stąd,
gdyby
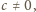 liczba
liczba
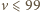 byłaby podzielna przez 100. Wobec tego
byłaby podzielna przez 100. Wobec tego
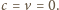 Wtedy mamy
Wtedy mamy
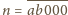 – wówczas
– wówczas

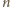 postaci
postaci
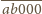 są wszystkimi liczbami
pięciocyfrowymi o własności z treści zadania.
są wszystkimi liczbami
pięciocyfrowymi o własności z treści zadania.
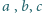 takie, że
takie, że
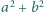 dzieli się przez
dzieli się przez

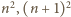 będą końcami danego przedziału. Wymagane warunki
spełniają na przykład liczby
będą końcami danego przedziału. Wymagane warunki
spełniają na przykład liczby
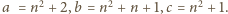 Rzeczywiście,
Rzeczywiście,
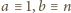 (mod
(mod
 ), więc
), więc
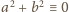 (mod
(mod
 ).
).
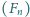 będzie ciągiem Fibonacciego:
będzie ciągiem Fibonacciego:

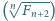 jest malejący.
jest malejący.
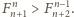 Dla
Dla
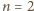 to prawda
to prawda
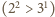 . Dalej przyjmujemy
. Dalej przyjmujemy
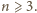 Korzystamy ze wzoru
Korzystamy ze wzoru
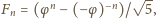 gdzie
gdzie
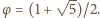 Oznaczmy:
Oznaczmy:
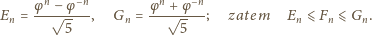
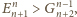 czyli
czyli
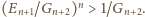 A ponieważ
A ponieważ
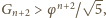 wystarczy dowieść, że
wystarczy dowieść, że
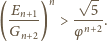
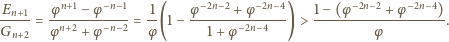
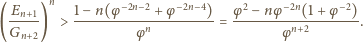
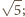 jest to równoważne nierówności
jest to równoważne nierówności
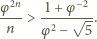
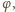 sprawdzamy, że nierówność (2)
zachodzi dla
sprawdzamy, że nierówność (2)
zachodzi dla
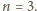 Zachodzi więc dla wszystkich
Zachodzi więc dla wszystkich
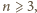 bo
wyrażenie po lewej stronie (2) przedstawia ciąg rosnący. To kończy
dowód.
bo
wyrażenie po lewej stronie (2) przedstawia ciąg rosnący. To kończy
dowód.
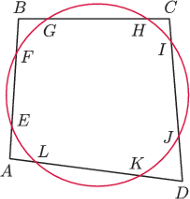
 przecina boki
przecina boki
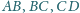 i
i
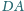 czworokąta
wypukłego
czworokąta
wypukłego
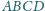 w punktach
w punktach
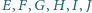 oraz
oraz
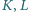 (patrz rysunek 3). Wykaż, że na czworokącie
(patrz rysunek 3). Wykaż, że na czworokącie
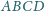 można opisać
okrąg wtedy i tylko wtedy, gdy suma długości łuków
można opisać
okrąg wtedy i tylko wtedy, gdy suma długości łuków
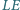 i
i
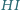 jest równa sumie długości łuków
jest równa sumie długości łuków
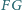 i
i
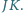
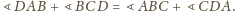 Z faktu
wnioskujemy, że
Z faktu
wnioskujemy, że
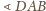 jest równy różnicy kątów wpisanych
w okrąg
jest równy różnicy kątów wpisanych
w okrąg
 i opartych na łukach
i opartych na łukach
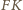 oraz
oraz
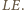 Podobnie
Podobnie
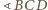 jest równy różnicy kątów wpisanych opartych na łukach
jest równy różnicy kątów wpisanych opartych na łukach
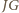 oraz
oraz
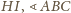 jest równy różnicy kątów wpisanych opartych
na łukach
jest równy różnicy kątów wpisanych opartych
na łukach
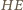 i
i
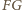 i
i
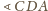 jest równy różnicy
kątów wpisanych opartych na łukach
jest równy różnicy
kątów wpisanych opartych na łukach
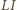 i
i
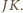 Oznaczmy przez
Oznaczmy przez
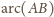 długość łuku
długość łuku
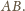 Zatem teza zadania zachodzi wtedy
i tylko wtedy, gdy
Zatem teza zadania zachodzi wtedy
i tylko wtedy, gdy
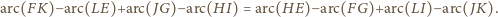
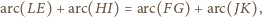
 płaszczyznami
przechodzącymi przez środki trzech jego krawędzi, z których żadne dwie nie
są równoległe i nie mają punktów wspólnych, są równe. Udowodnić, że
równoległościan
płaszczyznami
przechodzącymi przez środki trzech jego krawędzi, z których żadne dwie nie
są równoległe i nie mają punktów wspólnych, są równe. Udowodnić, że
równoległościan
 jest prostopadłościanem.
jest prostopadłościanem.
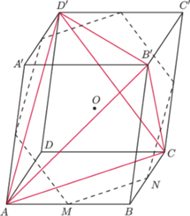
 będzie równoległościanem
będzie równoległościanem
 rozważanym
w zadaniu. Jak wiemy z poprzedniego odcinka, wystarczy, jeśli wykażemy, że
czworościan
rozważanym
w zadaniu. Jak wiemy z poprzedniego odcinka, wystarczy, jeśli wykażemy, że
czworościan
 wpisany w ten równoległościan jest
równościenny, a to będzie udowodnione, gdy uzasadnimy, że pola jego ścian
są równe.
wpisany w ten równoległościan jest
równościenny, a to będzie udowodnione, gdy uzasadnimy, że pola jego ścian
są równe.
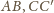 i
i
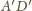 (rysunek). Nietrudno udowodnić, że
przekrój ten jest sześciokątem przechodzącym także przez środki
krawędzi
(rysunek). Nietrudno udowodnić, że
przekrój ten jest sześciokątem przechodzącym także przez środki
krawędzi
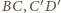 i
i
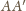 oraz zawierającym środek symetrii
oraz zawierającym środek symetrii
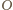 danego równoległościanu. Punkt
danego równoległościanu. Punkt
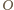 jest także środkiem
symetrii tego sześciokąta, więc pole rozważanego przekroju jest 6 razy
większe niż pole trójkąta
jest także środkiem
symetrii tego sześciokąta, więc pole rozważanego przekroju jest 6 razy
większe niż pole trójkąta
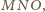 gdzie
gdzie
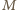 i
i
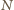 są
środkami odcinków
są
środkami odcinków
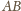 i
i
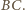 Z drugiej strony pole tego
trójkąta jest 4 razy mniejsze niż pole trójkąta
Z drugiej strony pole tego
trójkąta jest 4 razy mniejsze niż pole trójkąta
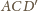 będącego
ścianą czworościanu
będącego
ścianą czworościanu
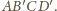 Stąd wniosek, że pole ściany
Stąd wniosek, że pole ściany
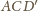 stanowi
stanowi
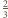 pola rozważanego przekroju.
pola rozważanego przekroju.
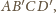 to z równości pól danych przekrojów
wynika równość pól ścian tego czworościanu – a to właśnie chcieliśmy
wykazać.
to z równości pól danych przekrojów
wynika równość pól ścian tego czworościanu – a to właśnie chcieliśmy
wykazać.
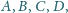 dla których spełnione są warunki:
dla których spełnione są warunki:

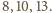 W poprzednim kąciku
jednak stwierdziliśmy, że ściany takiego czworościanu muszą być trójkątami
ostrokątnymi, zaś z nierówności
W poprzednim kąciku
jednak stwierdziliśmy, że ściany takiego czworościanu muszą być trójkątami
ostrokątnymi, zaś z nierówności
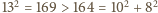 wynika,
że trójkąt o bokach
wynika,
że trójkąt o bokach
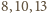 jest rozwartokątny. Zatem taka czwórka
punktów w przestrzeni nie istnieje.
jest rozwartokątny. Zatem taka czwórka
punktów w przestrzeni nie istnieje.
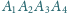 . Przez
. Przez
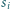 oznaczmy długość
odcinka będącego częścią wspólną środkowej czworościanu poprowadzonej
z wierzchołka
oznaczmy długość
odcinka będącego częścią wspólną środkowej czworościanu poprowadzonej
z wierzchołka
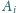 i kuli wpisanej w ten czworościan. Wiadomo, że
i kuli wpisanej w ten czworościan. Wiadomo, że
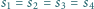 . Rozstrzygnąć, czy czworościan ten musi być
foremny.
. Rozstrzygnąć, czy czworościan ten musi być
foremny.
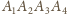 będzie dowolnym nieforemnym czworościanem
równościennym. Ponieważ odcinek łączący środki krawędzi
będzie dowolnym nieforemnym czworościanem
równościennym. Ponieważ odcinek łączący środki krawędzi
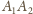 i
i
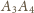 jest do nich prostopadły, to przekształcenie będące obrotem wokół
tego odcinka o
jest do nich prostopadły, to przekształcenie będące obrotem wokół
tego odcinka o
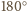 przeprowadza dany czworościan na siebie. W
szczególności kula wpisana w ten czworościan również musi przejść na
siebie. Przy tym przekształceniu punkt
przeprowadza dany czworościan na siebie. W
szczególności kula wpisana w ten czworościan również musi przejść na
siebie. Przy tym przekształceniu punkt
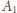 przechodzi na
przechodzi na
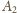 zaś
zaś
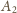 na
na
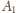 i podobnie
i podobnie
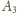 przechodzi na
przechodzi na
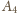 i
na odwrót. W takim razie środkowa poprowadzona z wierzchołka
i
na odwrót. W takim razie środkowa poprowadzona z wierzchołka
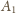 przechodzi na środkową poprowadzoną z wierzchołka
przechodzi na środkową poprowadzoną z wierzchołka
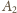 .
Skoro jednak kula wpisana jest zachowywana, to część wspólna jednej
środkowej z kulą przechodzi na część wspólną drugiej środkowej z tą
kulą. To oznacza, że
.
Skoro jednak kula wpisana jest zachowywana, to część wspólna jednej
środkowej z kulą przechodzi na część wspólną drugiej środkowej z tą
kulą. To oznacza, że
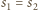 . Podobnie udowodnimy pozostałe
równości.
. Podobnie udowodnimy pozostałe
równości.