Numerowanie»Zadanie 4
o zadaniu...
- Zadanie pochodzi z artykułu Numerowanie
- Publikacja w Delcie: kwiecień 2011
- Publikacja elektroniczna: 31-03-2011
- Artykuł źródłowy w wersji do druku [application/pdf]: (109 KB)
Zadanie pochodzi z broszury Przed konkursem matematycznym Stowarzyszenia na rzecz Edukacji Matematycznej (Wyd. Szkolne Omega, Kraków 2010).
Na każdej ścianie sześcianu zapisano dodatnią liczbę całkowitą, a w każdym wierzchołku iloczyn liczb występujących na trzech ścianach z danym wierzchołkiem. Suma wszystkich liczb zapisanych w wierzchołkach tego sześcianu jest równa 2009. Jaka jest suma liczb zapisanych na jego ścianach?
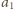 i
i
 i
i
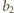 oraz
oraz
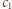 i
i
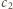 liczby zapisane na parach przeciwległych ścian sześcianu.
Zauważmy, że w każdym wierzchołku występuje inny spośród ośmiu
możliwych iloczynów
liczby zapisane na parach przeciwległych ścian sześcianu.
Zauważmy, że w każdym wierzchołku występuje inny spośród ośmiu
możliwych iloczynów
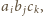 gdzie
gdzie
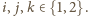 Suma liczb
w wierzchołkach jest więc sumą tych ośmiu iloczynów i można ją zapisać
jako
Suma liczb
w wierzchołkach jest więc sumą tych ośmiu iloczynów i można ją zapisać
jako
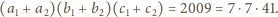
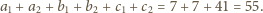
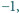 a każdej ścianie – iloczyn liczb przyporządkowanych wierzchołkom tej
ściany. Wyznacz zbiór wartości, które może przyjąć suma 14 liczb
przyporządkowanych ścianom i wierzchołkom.
a każdej ścianie – iloczyn liczb przyporządkowanych wierzchołkom tej
ściany. Wyznacz zbiór wartości, które może przyjąć suma 14 liczb
przyporządkowanych ścianom i wierzchołkom.
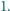 Udowodnij, że w tym czworościanie można umieścić 6 kul o promieniu
Udowodnij, że w tym czworościanie można umieścić 6 kul o promieniu
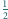 w taki sposób, aby każde dwie kule miały co najwyżej jeden punkt
wspólny.
w taki sposób, aby każde dwie kule miały co najwyżej jeden punkt
wspólny.
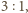 licząc od wierzchołka. Punkt ten jest jednocześnie środkiem kuli wpisanej i
opisanej na czworościanie foremnym.
licząc od wierzchołka. Punkt ten jest jednocześnie środkiem kuli wpisanej i
opisanej na czworościanie foremnym.
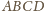 można wpisać kulę
można wpisać kulę
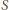 o środku
o środku
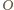 i promieniu 1, wysokość tego czworościanu wynosi 4
(na podstawie przytoczonej własności). Przekształćmy czworościan
foremny
i promieniu 1, wysokość tego czworościanu wynosi 4
(na podstawie przytoczonej własności). Przekształćmy czworościan
foremny
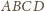 przez jednokładność względem punktu
przez jednokładność względem punktu
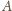 o skali
o skali
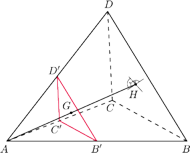
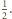 W efekcie otrzymamy czworościan
W efekcie otrzymamy czworościan
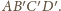 Korzystając z własności jednokładności, wnioskujemy, że płaszczyzna
Korzystając z własności jednokładności, wnioskujemy, że płaszczyzna
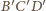 przecina wysokość
przecina wysokość
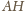 w punkcie
w punkcie
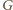 w taki
sposób, że
w taki
sposób, że
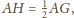 a kula
a kula
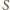 jest również styczna do
płaszczyzny
jest również styczna do
płaszczyzny
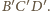 Zatem kula
Zatem kula
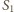 wpisana w czworościan
wpisana w czworościan
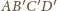 ma promień
ma promień
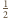 i ma tylko jeden punkt wspólny z kulą
i ma tylko jeden punkt wspólny z kulą
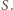
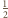 umieszczone w każdym „rogu” czworościanu
umieszczone w każdym „rogu” czworościanu
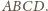 Każda z tych kul
ma tylko jeden punkt wspólny z kulą
Każda z tych kul
ma tylko jeden punkt wspólny z kulą
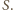 Ponieważ kula
Ponieważ kula
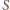 ma
promień 1, więc można umieścić w niej dwie kule o promieniu
ma
promień 1, więc można umieścić w niej dwie kule o promieniu
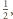 które mają tylko jeden punkt wspólny.
które mają tylko jeden punkt wspólny.
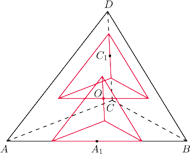
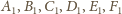 będą odpowiednio środkami krawędzi
będą odpowiednio środkami krawędzi
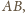
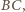
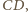
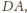
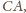
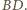 Przekształćmy kulę
Przekształćmy kulę
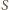 i czworościan
i czworościan
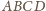 przez
przez 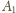 i skali
i skali
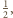
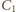 i skali
i skali
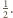
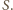 Zatem kule wpisane w te
czworościany nie mają punktów wspólnych.
Zatem kule wpisane w te
czworościany nie mają punktów wspólnych.
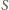 przez
przez 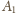 i skali
i skali
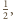
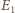 i skali
i skali
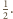
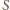 będą środki kul o promieniach
będą środki kul o promieniach
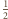 znajdujące się w połowie odcinków
znajdujące się w połowie odcinków
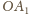 i
i
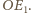 Wykażemy teraz,
że kule te nie mają punktów wspólnych.
Wykażemy teraz,
że kule te nie mają punktów wspólnych.
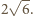 Zatem odległość
punktów
Zatem odległość
punktów
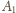 i
i
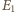 wynosi
wynosi
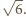 Środki boków
Środki boków
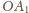 i
i
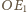 w trójkącie
w trójkącie
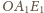 pozostają w odległości
pozostają w odległości
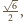 która
jest większa od 1.
która
jest większa od 1.
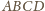 można umieścić sześć
kul: każda z nich jest obrazem kuli wpisanej w czworościan
można umieścić sześć
kul: każda z nich jest obrazem kuli wpisanej w czworościan
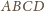 w
jednokładności o skali
w
jednokładności o skali
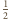 i środku będącym środkiem krawędzi
czworościanu.
i środku będącym środkiem krawędzi
czworościanu.
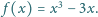 Definiujemy indukcyjnie
Definiujemy indukcyjnie
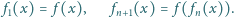
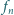 ma
ma
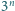 pierwiastków rzeczywistych.
pierwiastków rzeczywistych.
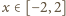 możemy napisać
możemy napisać
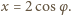
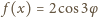
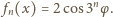
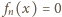 dla
dla
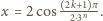 Ponieważ
funkcja
Ponieważ
funkcja
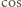 jest malejąca w przedziale
jest malejąca w przedziale
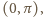 więc pierwiastki
otrzymane dla
więc pierwiastki
otrzymane dla
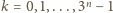 będą różne, a więcej pierwiastków
będą różne, a więcej pierwiastków
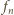 mieć nie może.
mieć nie może.
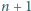 liczb ze zbioru
liczb ze zbioru
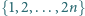 można wybrać dwie, tak żeby jedna była
dzielnikiem drugiej.
można wybrać dwie, tak żeby jedna była
dzielnikiem drugiej.
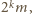 gdzie
gdzie
 jest nieparzyste.
Wówczas
jest nieparzyste.
Wówczas
 może przyjąć wartość
może przyjąć wartość
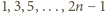 – łącznie
– łącznie
 różnych wartości. W takim razie, wśród dowolnych
różnych wartości. W takim razie, wśród dowolnych
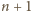 liczb znajdą się takie dwie, które mają ten sam czynnik nieparzysty, spełniają
więc warunek zadania.
liczb znajdą się takie dwie, które mają ten sam czynnik nieparzysty, spełniają
więc warunek zadania.
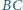 trójkąta
trójkąta
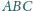 wybrano punkt
wybrano punkt
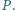 Punkty
Punkty
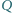 i
i
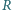 są środkami okręgów wpisanych w trójkąty
są środkami okręgów wpisanych w trójkąty
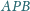 i
i
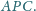 Punkt
Punkt
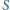 jest punktem styczności okręgu wpisanego w trójkąt
jest punktem styczności okręgu wpisanego w trójkąt
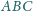 do boku
do boku
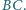 Wykazać, że punkty
Wykazać, że punkty
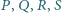 leżą na
jednym okręgu.
leżą na
jednym okręgu.
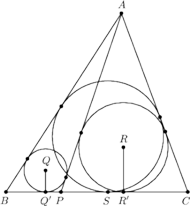
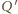 i
i
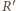 oznaczają rzuty punktów
oznaczają rzuty punktów
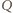 i
i
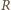 na
prostą
na
prostą
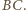 Z przyrównania odcinków stycznych do okręgu wpisanego
w trójkącie
Z przyrównania odcinków stycznych do okręgu wpisanego
w trójkącie
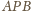 wynika równość
wynika równość
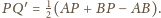 Podobnie mamy
Podobnie mamy
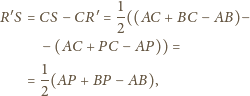
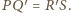 Stąd również
Stąd również
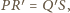 czyli
czyli
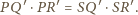
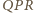 między dwusiecznymi kątów przyległych jest prosty,
więc trójkąty prostokątne
między dwusiecznymi kątów przyległych jest prosty,
więc trójkąty prostokątne
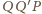 i
i
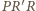 są podobne. W takim
razie
są podobne. W takim
razie
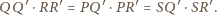
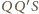 i
i
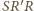 są podobne, więc kąt
są podobne, więc kąt
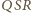 też
jest prosty. To oznacza, że punkty
też
jest prosty. To oznacza, że punkty
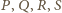 leżą na jednym
okręgu.
leżą na jednym
okręgu.
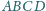 jest styczna do ścian
jest styczna do ścian
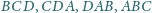 odpowiednio w punktach
odpowiednio w punktach
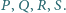 Odcinek
Odcinek
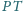 jest średnicą tej sfery, zaś punkty
jest średnicą tej sfery, zaś punkty
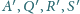 są
punktami przecięcia prostych
są
punktami przecięcia prostych
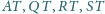 z płaszczyzną
z płaszczyzną
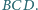 Dowieść , że punkt
Dowieść , że punkt
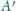 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie
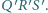
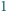 od jego wierzchołków jest
nie większa niż
od jego wierzchołków jest
nie większa niż
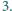
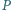 leżącego
wewnątrz trójkąta równobocznego
leżącego
wewnątrz trójkąta równobocznego
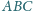 o boku
o boku
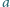 od jego
wierzchołków jest nie większa niż
od jego
wierzchołków jest nie większa niż
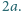
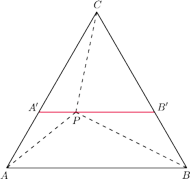
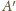 i
i
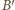 będą punktami przecięcia prostej równoległej
do
będą punktami przecięcia prostej równoległej
do
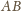 i przechodzącej przez punkt
i przechodzącej przez punkt
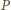 odpowiednio z bokami
odpowiednio z bokami
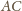 i
i
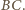 Trójkąt
Trójkąt
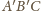 jest równoboczny i
jest równoboczny i
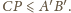 Ponadto stosując nierówność trójkąta, dostaniemy
Ponadto stosując nierówność trójkąta, dostaniemy
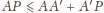 oraz
oraz
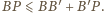 Dodając te trzy nierówności stronami,
otrzymujemy
Dodając te trzy nierówności stronami,
otrzymujemy
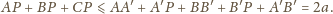
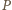 jest jednym z wierzchołków trójkąta
jest jednym z wierzchołków trójkąta
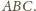
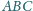 jest styczny do boków
jest styczny do boków
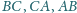 odpowiednio w punktach
odpowiednio w punktach
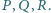 Odcinek
Odcinek
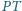 jest średnicą tego
okręgu. Proste
jest średnicą tego
okręgu. Proste
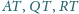 przecinają prostą
przecinają prostą
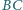 odpowiednio
w punktach
odpowiednio
w punktach
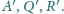 Wykazać, że
Wykazać, że
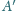 jest środkiem odcinka
jest środkiem odcinka
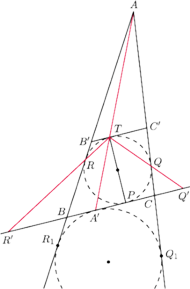
 jest średnicą, to styczna do okręgu wpisanego w punkcie
jest średnicą, to styczna do okręgu wpisanego w punkcie
 jest równoległa do
jest równoległa do
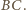 Niech
Niech
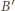 i
i
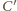 będą punktami
przecięcia tej stycznej z bokami
będą punktami
przecięcia tej stycznej z bokami
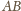 i
i
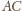 (
(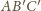 i
i
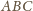 są jednokładne, skąd natychmiast wynika, że
punkt
są jednokładne, skąd natychmiast wynika, że
punkt
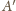 jest punktem styczności okręgu dopisanego z bokiem
jest punktem styczności okręgu dopisanego z bokiem
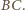 Z równoległości
Z równoległości
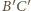 i
i
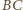 wynika też, że trójkąty
wynika też, że trójkąty
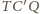 i
i
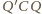 są podobne, a skoro
są podobne, a skoro
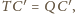 to
to
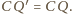 Niech
Niech
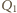 będzie punktem styczności okręgu
dopisanego, stycznego do
będzie punktem styczności okręgu
dopisanego, stycznego do
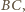 z prostą
z prostą
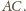 W takim razie
W takim razie
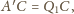 a stąd natychmiast wynika, że
a stąd natychmiast wynika, że
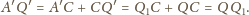
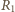 punkt styczności okręgu dopisanego
z bokiem
punkt styczności okręgu dopisanego
z bokiem
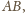 udowodnimy, że
udowodnimy, że
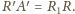 Ale
Ale
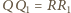 – dowód jest więc zakończony.
– dowód jest więc zakończony.
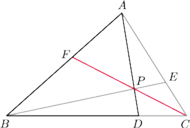
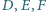 należą odpowiednio do boków
należą odpowiednio do boków
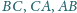 trójkąta
trójkąta
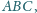 proste
proste
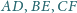 przecinają się w punkcie
przecinają się w punkcie
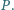 Wykaż, że
Wykaż, że

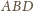 i prostej
i prostej
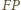 zachodzi
zachodzi
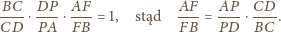
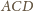 i prostej
i prostej
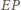 otrzymujemy
otrzymujemy

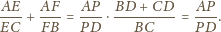
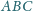 punkty
punkty
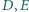 są spodkami dwusiecznych
odpowiednio
są spodkami dwusiecznych
odpowiednio
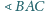 i
i
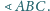 Punkt
Punkt
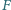 jest spodkiem
dwusiecznej kąta zewnętrznego przy wierzchołku
jest spodkiem
dwusiecznej kąta zewnętrznego przy wierzchołku
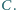 Udowodnij, że
punkty
Udowodnij, że
punkty
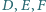 leżą na jednej prostej.
leżą na jednej prostej.
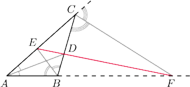
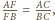
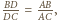
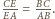 Zachodzi więc równość z Twierdzenie Menelaosa, co
kończy dowód.
Zachodzi więc równość z Twierdzenie Menelaosa, co
kończy dowód.
 jest styczna do krawędzi
jest styczna do krawędzi
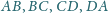 czworościanu
czworościanu
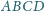 dpowiednio w punktach
dpowiednio w punktach
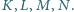 Wykaż, że leżą one
na jednej płaszczyźnie.
Wykaż, że leżą one
na jednej płaszczyźnie.
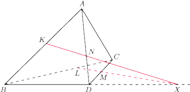
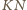 przecina prostą
przecina prostą
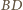 w pewnym punkcie
w pewnym punkcie
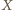 (poza odcinkiem
(poza odcinkiem
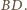 Wtedy z twierdzenia Menelaosa dla
trójkąta
Wtedy z twierdzenia Menelaosa dla
trójkąta
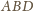 i prostej
i prostej
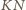 mamy
mamy
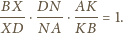
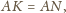
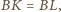
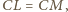
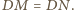 Wobec powyższego
Wobec powyższego
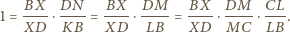
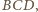 prosta
prosta
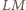 przecina prostą
przecina prostą
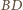 w punkcie
w punkcie
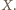 Stąd proste
Stąd proste
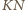 i
i
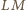 przecinają się, więc punkty
przecinają się, więc punkty
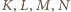 leżą na jednej
płaszczyźnie. Prostszy przypadek
leżą na jednej
płaszczyźnie. Prostszy przypadek
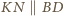 pozostawiam jako
ćwiczenie.
pozostawiam jako
ćwiczenie.
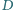 i
i
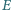 leżą odpowiednio na bokach
leżą odpowiednio na bokach
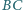 i
i
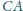 trójkąta
trójkąta
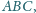 a punkt
a punkt
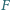 na przedłużeniu boku
na przedłużeniu boku
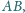 przy czym punkty
przy czym punkty
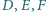 są współliniowe. Punkty
są współliniowe. Punkty
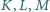 są odpowiednio środkami boków
są odpowiednio środkami boków
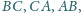 zaś punkty
zaś punkty
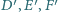 – obrazami symetrycznymi punktów
– obrazami symetrycznymi punktów
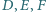 w symetriach względem
w symetriach względem
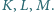 Wykaż, że punkty
Wykaż, że punkty
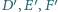 są
współliniowe.
są
współliniowe.
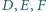
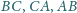
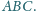
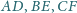

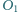 i skali
i skali
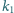 z jednokładnością o środku
z jednokładnością o środku
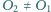 i skali
i skali
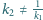 jest
jednokładnością o środku na prostej
jest
jednokładnością o środku na prostej
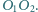
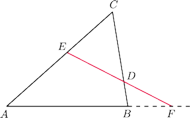
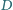
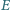
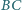
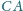
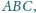
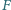
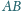
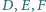
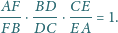
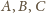 na prostą
na prostą
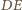 i zastosuj twierdzenie
Talesa.
i zastosuj twierdzenie
Talesa.
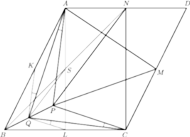
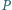 leży wewnątrz równoległoboku
leży wewnątrz równoległoboku
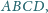 przy czym
środek odcinka
przy czym
środek odcinka
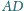 jest jednakowo odległy od punktów
jest jednakowo odległy od punktów
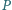 i
i
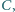 a środek odcinka
a środek odcinka
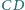 jest jednakowo odległy od punktów
jest jednakowo odległy od punktów
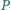 i
i
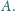 Punkt
Punkt
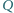 jest środkiem odcinka
jest środkiem odcinka
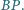 Wykazać, że
Wykazać, że
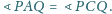
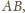
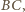
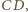
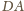 odpowiednio przez
odpowiednio przez
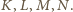 W myśl założenia,
W myśl założenia,
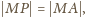
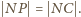 Niech
Niech
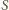 będzie wspólnym środkiem przekątnych
będzie wspólnym środkiem przekątnych
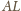 i
i
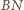 równoległoboku
równoległoboku
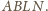 Odcinek
Odcinek
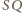 łączy środki
dwóch boków trójkąta
łączy środki
dwóch boków trójkąta
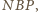 więc
więc
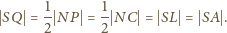
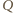 leży na okręgu o średnicy
leży na okręgu o średnicy
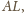 wobec czego kąt
wobec czego kąt
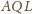 jest prosty. Analogicznie, kąt
jest prosty. Analogicznie, kąt
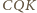 jest prosty. Stąd
wynika, że
jest prosty. Stąd
wynika, że
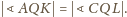 Punkty
Punkty
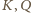 są środkami
dwóch boków trójkąta
są środkami
dwóch boków trójkąta
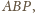 więc
więc
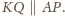 Analogicznie,
Analogicznie,
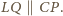 Stąd, ostatecznie,
Stąd, ostatecznie,
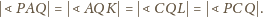
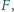 określone na zbiorze wszystkich
liczb całkowitych dodatnich, o wartościach rzeczywistych, spełniające
równanie
określone na zbiorze wszystkich
liczb całkowitych dodatnich, o wartościach rzeczywistych, spełniające
równanie
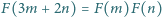 dla każdej pary liczb
całkowitych
dla każdej pary liczb
całkowitych
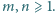
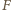 będzie jedną z szukanych funkcji. Oznaczmy wartości
będzie jedną z szukanych funkcji. Oznaczmy wartości
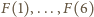 kolejno przez
kolejno przez
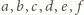 ; oznaczmy ponadto
; oznaczmy ponadto
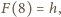
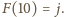 Kładąc w równaniu
Kładąc w równaniu
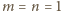 oraz
oraz
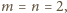 dostajemy
dostajemy

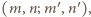 w której
w której
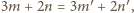 daje
informację w postaci równości
daje
informację w postaci równości
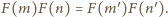 Biorąc czwórki
Biorąc czwórki
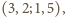
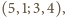
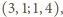
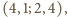
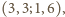 otrzymujemy
w ten sposób związki
otrzymujemy
w ten sposób związki
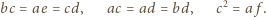
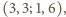
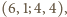
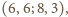
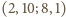 dają
zależności
dają
zależności
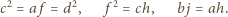
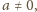 to z pierwszej równości (1) oraz ze związków (2)
wnosimy kolejno, że
to z pierwszej równości (1) oraz ze związków (2)
wnosimy kolejno, że
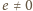 ;
;
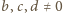 ;
;
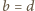 ;
;
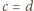 ;
;
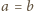 ;
;
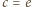 ;
;
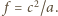 Tak więc
Tak więc
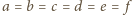 ;
skoro zaś
;
skoro zaś
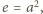 ta wspólna wartość wynosi 1.
ta wspólna wartość wynosi 1.
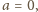 to korzystamy z zależności (3) oraz (1) i łatwo
stwierdzamy, że
to korzystamy z zależności (3) oraz (1) i łatwo
stwierdzamy, że
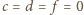 ;
;
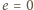 ;
;
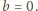 Zatem na
zbiorze
Zatem na
zbiorze
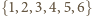 funkcja
funkcja
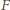 jest stała, o wartości
1 lub 0. Każda liczba naturalna
jest stała, o wartości
1 lub 0. Każda liczba naturalna
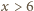 daje się zapisać w postaci
daje się zapisać w postaci
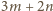 dla pewnych
dla pewnych
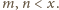 Przez oczywistą indukcję
uzyskujemy wniosek, że
Przez oczywistą indukcję
uzyskujemy wniosek, że
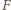 jest funkcją tożsamościowo równą
1 lub 0. Każda z nich spełnia zadane równanie.
jest funkcją tożsamościowo równą
1 lub 0. Każda z nich spełnia zadane równanie.
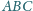 obrano punkt
obrano punkt
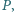 taki że
taki że
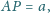

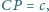 gdzie
gdzie
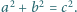 Wyznaczyć długość boku trójkąta
Wyznaczyć długość boku trójkąta
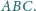
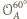 oraz punkt
oraz punkt
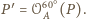 Zauważmy, że
Zauważmy, że
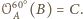 Tak więc
Tak więc
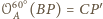 i w szczególności
i w szczególności
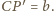 Trójkąt
Trójkąt
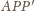 jest równoboczny, więc
jest równoboczny, więc
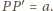 Z założeń wynika, iż
Z założeń wynika, iż
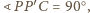 czyli
czyli
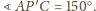 Stosując twierdzenie kosinusów
do trójkąta
Stosując twierdzenie kosinusów
do trójkąta
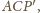 uzyskujemy
uzyskujemy