Nie tracimy ogólności, rozważając jedynie niemalejące ciągi 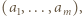 dzięki czemu wyrazy sumy
dzięki czemu wyrazy sumy
 |
(1) |
są uporządkowane nierosnąco. Niech 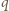 oraz
oraz  oznaczają iloraz i resztę z dzielenia
oznaczają iloraz i resztę z dzielenia 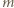 przez
przez 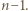 Wykażemy, że ciąg
Wykażemy, że ciąg
 |
(2) |
jest tym, dla którego suma (1) - pozostając mniejszą od 1 - jest maksymalna. Wynosi ona
 |
(3) |
Niech więc 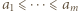 będzie dowolnym ciągiem, dla którego wartość sumy (1) jest mniejsza od 1. Przypuśćmy, że pewien wyraz
będzie dowolnym ciągiem, dla którego wartość sumy (1) jest mniejsza od 1. Przypuśćmy, że pewien wyraz 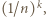 z wykładnikiem
z wykładnikiem 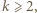 powtarza się co najmniej
powtarza się co najmniej 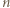 razy. Przyjmijmy, że
razy. Przyjmijmy, że 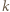 jest największym takim numerem. Wykreślamy
jest największym takim numerem. Wykreślamy 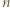 składników równych
składników równych 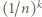 i zastępujemy je pojedynczym wyrazem
i zastępujemy je pojedynczym wyrazem 
Wartość sumy nie uległa zmianie, ale ciąg skrócił się o 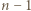 wyrazów. Dopisujemy więc na końcu
wyrazów. Dopisujemy więc na końcu 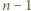 ułamków, z wykładnikami tak dużymi, by wartość sumy (1) (która się powiększa!) pozostała mniejsza od 1 - bacząc jedynie, by żaden wyraz (z wykładnikiem
ułamków, z wykładnikami tak dużymi, by wartość sumy (1) (która się powiększa!) pozostała mniejsza od 1 - bacząc jedynie, by żaden wyraz (z wykładnikiem 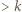 ) nie powtórzył się
) nie powtórzył się 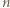 -krotnie.
-krotnie.
Powtarzamy tę modyfikację tak długo, dopóki istnieje blok jednakowych składników 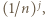 długości co najmniej
długości co najmniej 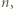 z jakimkolwiek wykładnikiem
z jakimkolwiek wykładnikiem 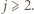 Mógłby ewentualnie pozostać taki blok dla wykładnika
Mógłby ewentualnie pozostać taki blok dla wykładnika 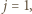 czyli złożony ze składników równych
czyli złożony ze składników równych 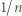 - ale to też nie jest możliwe, skoro przez cały czas była prowadzona kontrola, by suma nie osiągnęła wartości 1. Stąd wynika, że w dalszym ciągu dowodu można ograniczać uwagę do ciągów
- ale to też nie jest możliwe, skoro przez cały czas była prowadzona kontrola, by suma nie osiągnęła wartości 1. Stąd wynika, że w dalszym ciągu dowodu można ograniczać uwagę do ciągów 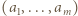 o własnościach:
o własnościach:
 |
(4) |
Ciąg (2) spełnia te warunki. Dla wykazania jego optymalności weźmy pod uwagę dowolny inny ciąg 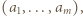 także spełniający powyższe warunki, i oznaczmy przez
także spełniający powyższe warunki, i oznaczmy przez 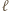 najwcześniejszy numer, dla którego
najwcześniejszy numer, dla którego 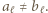 Zatem odcinki
Zatem odcinki 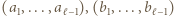 są identyczne.
są identyczne.
Nietrudno zauważyć, że 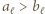 ; w przeciwnym przypadku mielibyśmy
; w przeciwnym przypadku mielibyśmy 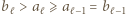 ; to by oznaczało, że
; to by oznaczało, że 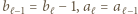 i że w ciągu (2)
i że w ciągu (2) 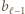 jest wyrazem kończącym blok złożony z
jest wyrazem kończącym blok złożony z 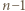 równych liczb. Skoro zaś
równych liczb. Skoro zaś 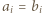 dla
dla 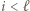 oraz
oraz 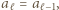 mielibyśmy w ciągu
mielibyśmy w ciągu 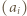 blok złożony z
blok złożony z  równych liczb, wbrew warunkowi (4). Tak więc
równych liczb, wbrew warunkowi (4). Tak więc 
Dokonujemy kolejnej modyfikacji ciągu 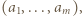 zastępując wyraz
zastępując wyraz 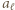 liczbą
liczbą 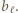 Warunki (4) pozostają spełnione, wartość sumy (1) zwiększa się, zaś nowy ciąg pokrywa się z ciągiem (2) na odcinku
Warunki (4) pozostają spełnione, wartość sumy (1) zwiększa się, zaś nowy ciąg pokrywa się z ciągiem (2) na odcinku 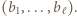 Po skończenie wielu takich krokach dochodzimy do ciągu
Po skończenie wielu takich krokach dochodzimy do ciągu 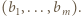 To pokazuje, że wartość sumy (1) dla wyjściowego ciągu
To pokazuje, że wartość sumy (1) dla wyjściowego ciągu 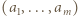 była mniejsza niż jej wartość dla ciągu
była mniejsza niż jej wartość dla ciągu 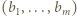 - czyli liczba dana wzorem (3), która wobec tego jest szukanym kresem górnym.
- czyli liczba dana wzorem (3), która wobec tego jest szukanym kresem górnym.
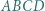 o osi symetrii
o osi symetrii 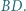 Punkty
Punkty 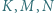 są odpowiednio punktami styczności okręgu wpisanego z bokami
są odpowiednio punktami styczności okręgu wpisanego z bokami 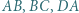 ; proste
; proste 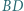 i
i 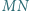 przecinają się w punkcie
przecinają się w punkcie 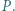 Wykaż, że punkty
Wykaż, że punkty 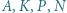 leżą na jednym okręgu.
leżą na jednym okręgu.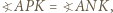 korzystając np. z
korzystając np. z 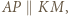 z równoramienności trójkąta
z równoramienności trójkąta 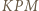 i z twierdzenia o stycznej i cięciwie.
i z twierdzenia o stycznej i cięciwie.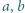 i
i 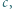 które spełniałyby równość
które spełniałyby równość 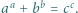
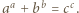 Bez straty ogólności
Bez straty ogólności 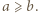 Można z tego wywnioskować nierówność
Można z tego wywnioskować nierówność 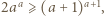 która prowadzi do sprzeczności.
która prowadzi do sprzeczności.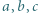 oraz
oraz 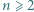 spełniają równość
spełniają równość 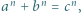 to
to 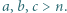
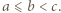 Należy uzasadnić i wykorzystać nierówność
Należy uzasadnić i wykorzystać nierówność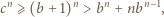
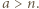
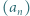 liczb naturalnych spełnia warunki
liczb naturalnych spełnia warunki 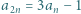 i
i 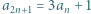 dla wszystkich naturalnych
dla wszystkich naturalnych 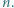 Dowieść, że jest to ciąg rosnący.
Dowieść, że jest to ciąg rosnący.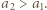 Załóżmy indukcyjnie, przy ustalonym
Załóżmy indukcyjnie, przy ustalonym 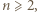 że
że 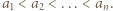 Trzeba dowieść, że
Trzeba dowieść, że 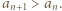 Należy tu rozważyć dwa przypadki:
Należy tu rozważyć dwa przypadki: 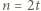 oraz
oraz 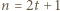 dla pewnego całkowitego dodatniego
dla pewnego całkowitego dodatniego 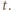 Pierwszy przypadek jest natychmiastowy i nie wymaga nawet skorzystania z założenia indukcyjnego. W drugim korzystamy z nierówności
Pierwszy przypadek jest natychmiastowy i nie wymaga nawet skorzystania z założenia indukcyjnego. W drugim korzystamy z nierówności 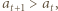 którą zapiszemy w postaci
którą zapiszemy w postaci 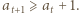
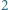 można przedstawić w postaci iloczynu trzech liczb naturalnych większych od
można przedstawić w postaci iloczynu trzech liczb naturalnych większych od 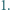
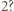
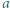 i
i 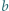 są naturalne. Dowieść, że istnieje taka liczba naturalna
są naturalne. Dowieść, że istnieje taka liczba naturalna 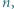 dla której
dla której 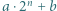 nie jest kwadratem liczby naturalnej.
nie jest kwadratem liczby naturalnej.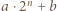 jest kwadratem dla każdego naturalnego
jest kwadratem dla każdego naturalnego 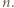 Wtedy liczby
Wtedy liczby 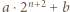 i
i 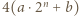 też są kwadratami, a różnica między nimi dla odpowiednio dużych
też są kwadratami, a różnica między nimi dla odpowiednio dużych  jest za mała.
jest za mała.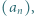 który spełnia warunki:
który spełnia warunki:

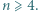
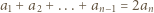
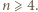 Z tego trzeba wywnioskować równość
Z tego trzeba wywnioskować równość 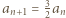 dla wszystkich
dla wszystkich 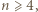 a to prowadzi do sprzeczności.
a to prowadzi do sprzeczności. zachodzi podzielność
zachodzi podzielność
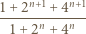
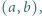 dla których liczby
dla których liczby 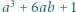 i
i 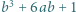 są sześcianami liczb naturalnych.
są sześcianami liczb naturalnych.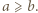 Wtedy
Wtedy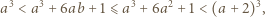
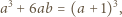
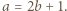 Podstawiając tę wartość, uzyskujemy oszacowania
Podstawiając tę wartość, uzyskujemy oszacowania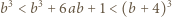
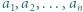 będą liczbami naturalnymi. Dowieść, że
będą liczbami naturalnymi. Dowieść, że
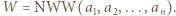 Liczby
Liczby 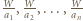 są naturalne i różne.
są naturalne i różne.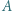 stanowi
stanowi 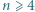 liczb naturalnych, przy czym spełniony jest warunek
liczb naturalnych, przy czym spełniony jest warunek 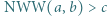 dla wszystkich parami różnych
dla wszystkich parami różnych 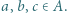 Dowieść, że suma odwrotności elementów zbioru
Dowieść, że suma odwrotności elementów zbioru 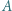 jest mniejsza od
jest mniejsza od 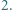
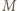 będzie największą liczbą w zbiorze
będzie największą liczbą w zbiorze 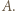 Każde
Każde 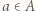 ma
ma 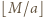 wielokrotności, które nie przekraczają
wielokrotności, które nie przekraczają 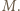 Z treści zadania wynika, że wszystkie te wielokrotności są różne.
Z treści zadania wynika, że wszystkie te wielokrotności są różne.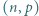 o tej własności, że
o tej własności, że 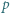 jest liczbą pierwszą większą od
jest liczbą pierwszą większą od 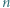 oraz
oraz 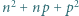 jest kwadratem liczby całkowitej.
jest kwadratem liczby całkowitej.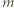 będzie taką dodatnią liczbą całkowitą, że
będzie taką dodatnią liczbą całkowitą, że 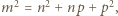 czyli
czyli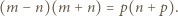
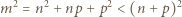
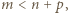 czyli
czyli 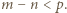 W szczególności liczba
W szczególności liczba 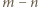 nie jest podzielna przez
nie jest podzielna przez 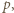 skąd wobec podzielności iloczynu
skąd wobec podzielności iloczynu 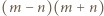 przez
przez 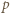 uzyskujemy
uzyskujemy 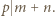 Ponadto skoro
Ponadto skoro 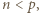 to
to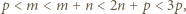
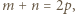 czyli
czyli 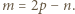 Zatem
Zatem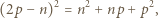
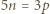 i wobec pierwszości liczby
i wobec pierwszości liczby 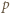 prowadzi do wniosku, że
prowadzi do wniosku, że 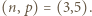 Jest to jedyna para o zadanych własnościach.
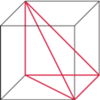
Jest to jedyna para o zadanych własnościach.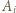 będzie wierzchołkiem kostki, odległym od stołu o
będzie wierzchołkiem kostki, odległym od stołu o 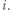 Oznaczmy długość krawędzi kostki przez
Oznaczmy długość krawędzi kostki przez  Łatwo zauważyć, że odcinki
Łatwo zauważyć, że odcinki 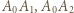 oraz
oraz 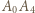 muszą być krawędziami sześcianu (wynika to z faktu, że jeśli krawędziami są
muszą być krawędziami sześcianu (wynika to z faktu, że jeśli krawędziami są 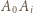 i
i 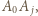 to
to 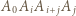 jest ścianą). Niech
jest ścianą). Niech 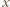 będzie długością krawędzi sześcianu. Dobierzmy układ współrzędnych tak, by
będzie długością krawędzi sześcianu. Dobierzmy układ współrzędnych tak, by 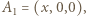
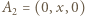 i
i 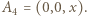 Oznaczmy przez
Oznaczmy przez 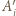 rzut prostokątny punktu
rzut prostokątny punktu 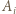 na prostą prostopadłą do stołu, przechodzącą przez
na prostą prostopadłą do stołu, przechodzącą przez 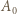 ; wówczas
; wówczas 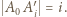 Przyjmijmy
Przyjmijmy 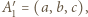 wtedy
wtedy 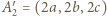 i
i 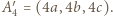 Korzystając z twierdzenia Pitagorasa dla trójkątów prostokątnych
Korzystając z twierdzenia Pitagorasa dla trójkątów prostokątnych 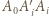 dla
dla 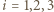 dostajemy
dostajemy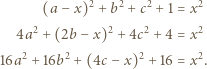
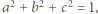 dostajemy
dostajemy 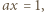
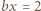 i
i 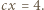 Po podniesieniu ostatnich trzech równości do kwadratu i zsumowaniu, otrzymamy
Po podniesieniu ostatnich trzech równości do kwadratu i zsumowaniu, otrzymamy 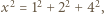 zatem
zatem 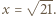
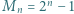 dla
dla 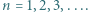 Udowodnić, że następujące dwa warunki są równoważne:
Udowodnić, że następujące dwa warunki są równoważne: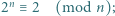
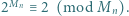
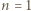 oba warunki są spełnione. Dalej przyjmujemy
oba warunki są spełnione. Dalej przyjmujemy 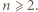 Zapiszmy liczbę
Zapiszmy liczbę 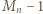 jako
jako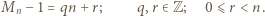
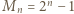 mamy kongruencję
mamy kongruencję 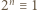 (mod
(mod 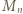 ), którą podnosimy do potęgi
), którą podnosimy do potęgi 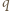 :
: 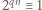 (mod
(mod 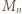 ); stąd po pomnożeniu przez
); stąd po pomnożeniu przez 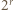 (i uwzględnieniu (1)):
(i uwzględnieniu (1)):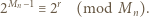
 jest dzielnikiem liczby
jest dzielnikiem liczby 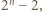 równej
równej 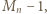 czyli w równości (1) jest
czyli w równości (1) jest 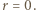 Ze związku (2) dostajemy
Ze związku (2) dostajemy 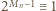 (mod
(mod 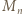 ); pomnożenie przez 2 daje warunek (ii).
); pomnożenie przez 2 daje warunek (ii).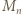 ) dzielimy stronami przez 2 (to dozwolone, bo
) dzielimy stronami przez 2 (to dozwolone, bo 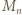 jest liczbą nieparzystą), otrzymując
jest liczbą nieparzystą), otrzymując 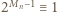 (mod
(mod 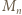 ). W połączeniu z (2) dostajemy
). W połączeniu z (2) dostajemy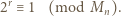
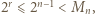 więc kongruencja (3) jest równością, skąd
więc kongruencja (3) jest równością, skąd 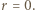 To znaczy, w myśl (1), że
To znaczy, w myśl (1), że  dzieli liczbę
dzieli liczbę 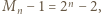 i mamy warunek (i).
i mamy warunek (i).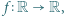 spełniające równanie
spełniające równanie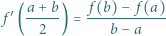
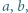 których różnica jest liczbą całkowitą.
których różnica jest liczbą całkowitą.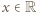 uzyskujemy z podanego równania (po podstawieniu
uzyskujemy z podanego równania (po podstawieniu 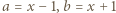 ) równość
) równość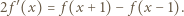
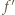 jest różniczkowalna. Możemy więc zróżniczkować (1) stronami, otrzymując
jest różniczkowalna. Możemy więc zróżniczkować (1) stronami, otrzymując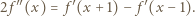
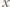 przez
przez 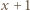 oraz
oraz 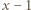 :
: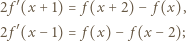
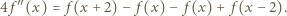
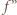 ma pochodną. Różniczkujemy (3) stronami:
ma pochodną. Różniczkujemy (3) stronami: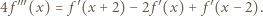
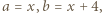 następnie
następnie 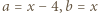 i wreszcie
i wreszcie 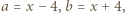 otrzymując kolejno
otrzymując kolejno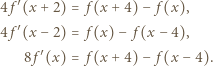
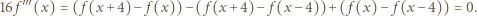
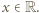 To znaczy, że
To znaczy, że 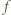 jest wielomianem stopnia najwyżej drugiego.
jest wielomianem stopnia najwyżej drugiego.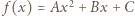 spełnia równanie dane w założeniu zadania (i to nawet dla każdej pary różnych liczb
spełnia równanie dane w założeniu zadania (i to nawet dla każdej pary różnych liczb 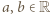 ) - co łatwo sprawdzić.
) - co łatwo sprawdzić.
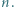
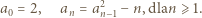
 warunek
warunek 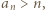 co można sprawdzić indukcyjnie: dla 1, 2 i 3 sprawdzamy bezpośrednio, ponadto jeśli
co można sprawdzić indukcyjnie: dla 1, 2 i 3 sprawdzamy bezpośrednio, ponadto jeśli 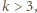 to mamy
to mamy 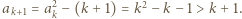 Kolejno otrzymujemy zatem
Kolejno otrzymujemy zatem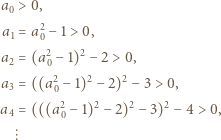
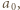 otrzymujemy kolejno
otrzymujemy kolejno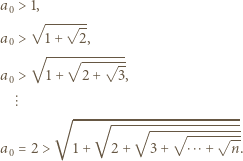

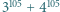 jest podzielna przez 13, 49, 181, 379, a nie jest podzielna przez 5 ani 11.
jest podzielna przez 13, 49, 181, 379, a nie jest podzielna przez 5 ani 11.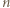 jest nieparzyste,
jest nieparzyste, 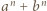 dzieli się przez
dzieli się przez 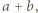 i wystarczy zauważyć, że
i wystarczy zauważyć, że 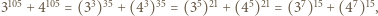 a więc
a więc 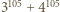 dzieli się przez
dzieli się przez 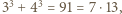 przez
przez 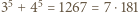 oraz przez
oraz przez 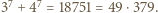
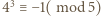 i
i 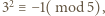 podobnie
podobnie 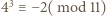 i
i 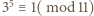 ).
).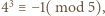 to
to 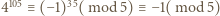 ; podobnie z
; podobnie z 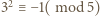 wynika
wynika 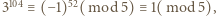 a więc
a więc 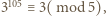 skąd
skąd 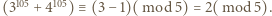
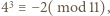 więc
więc 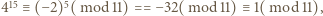 stąd
stąd 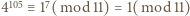 ; podobnie z
; podobnie z 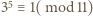 mamy
mamy 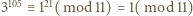 ; wobec tego
; wobec tego 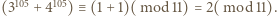
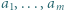 oraz
oraz 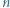 rozważamy sumę
rozważamy sumę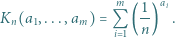
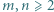 wyznaczyć kres górny zbioru tych wartości wyrażenia
wyznaczyć kres górny zbioru tych wartości wyrażenia 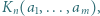 które są mniejsze od 1.
które są mniejsze od 1.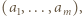 dzięki czemu wyrazy sumy
dzięki czemu wyrazy sumy
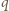 oraz
oraz  oznaczają iloraz i resztę z dzielenia
oznaczają iloraz i resztę z dzielenia 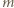 przez
przez 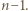 Wykażemy, że ciąg
Wykażemy, że ciąg

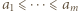 będzie dowolnym ciągiem, dla którego wartość sumy (1) jest mniejsza od 1. Przypuśćmy, że pewien wyraz
będzie dowolnym ciągiem, dla którego wartość sumy (1) jest mniejsza od 1. Przypuśćmy, że pewien wyraz 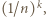 z wykładnikiem
z wykładnikiem 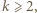 powtarza się co najmniej
powtarza się co najmniej 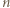 razy. Przyjmijmy, że
razy. Przyjmijmy, że 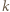 jest największym takim numerem. Wykreślamy
jest największym takim numerem. Wykreślamy 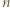 składników równych
składników równych 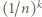 i zastępujemy je pojedynczym wyrazem
i zastępujemy je pojedynczym wyrazem 
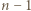 wyrazów. Dopisujemy więc na końcu
wyrazów. Dopisujemy więc na końcu 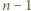 ułamków, z wykładnikami tak dużymi, by wartość sumy (1) (która się powiększa!) pozostała mniejsza od 1 - bacząc jedynie, by żaden wyraz (z wykładnikiem
ułamków, z wykładnikami tak dużymi, by wartość sumy (1) (która się powiększa!) pozostała mniejsza od 1 - bacząc jedynie, by żaden wyraz (z wykładnikiem 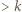 ) nie powtórzył się
) nie powtórzył się 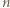 -krotnie.
-krotnie.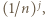 długości co najmniej
długości co najmniej 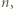 z jakimkolwiek wykładnikiem
z jakimkolwiek wykładnikiem 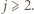 Mógłby ewentualnie pozostać taki blok dla wykładnika
Mógłby ewentualnie pozostać taki blok dla wykładnika 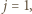 czyli złożony ze składników równych
czyli złożony ze składników równych 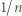 - ale to też nie jest możliwe, skoro przez cały czas była prowadzona kontrola, by suma nie osiągnęła wartości 1. Stąd wynika, że w dalszym ciągu dowodu można ograniczać uwagę do ciągów
- ale to też nie jest możliwe, skoro przez cały czas była prowadzona kontrola, by suma nie osiągnęła wartości 1. Stąd wynika, że w dalszym ciągu dowodu można ograniczać uwagę do ciągów 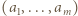 o własnościach:
o własnościach:
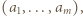 także spełniający powyższe warunki, i oznaczmy przez
także spełniający powyższe warunki, i oznaczmy przez 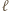 najwcześniejszy numer, dla którego
najwcześniejszy numer, dla którego 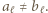 Zatem odcinki
Zatem odcinki 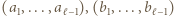 są identyczne.
są identyczne.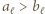 ; w przeciwnym przypadku mielibyśmy
; w przeciwnym przypadku mielibyśmy 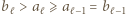 ; to by oznaczało, że
; to by oznaczało, że 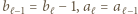 i że w ciągu (2)
i że w ciągu (2) 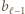 jest wyrazem kończącym blok złożony z
jest wyrazem kończącym blok złożony z 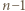 równych liczb. Skoro zaś
równych liczb. Skoro zaś 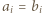 dla
dla 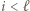 oraz
oraz 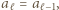 mielibyśmy w ciągu
mielibyśmy w ciągu 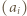 blok złożony z
blok złożony z  równych liczb, wbrew warunkowi (4). Tak więc
równych liczb, wbrew warunkowi (4). Tak więc 
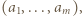 zastępując wyraz
zastępując wyraz 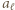 liczbą
liczbą 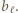 Warunki (4) pozostają spełnione, wartość sumy (1) zwiększa się, zaś nowy ciąg pokrywa się z ciągiem (2) na odcinku
Warunki (4) pozostają spełnione, wartość sumy (1) zwiększa się, zaś nowy ciąg pokrywa się z ciągiem (2) na odcinku 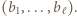 Po skończenie wielu takich krokach dochodzimy do ciągu
Po skończenie wielu takich krokach dochodzimy do ciągu 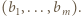 To pokazuje, że wartość sumy (1) dla wyjściowego ciągu
To pokazuje, że wartość sumy (1) dla wyjściowego ciągu 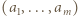 była mniejsza niż jej wartość dla ciągu
była mniejsza niż jej wartość dla ciągu 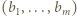 - czyli liczba dana wzorem (3), która wobec tego jest szukanym kresem górnym.
- czyli liczba dana wzorem (3), która wobec tego jest szukanym kresem górnym.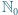 oznacza zbiór nieujemnych liczb całkowitych.
oznacza zbiór nieujemnych liczb całkowitych.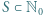 o tej własności, że każdy element zbioru
o tej własności, że każdy element zbioru 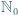 ma dokładnie jedno przedstawienie w postaci sumy dwóch (niekoniecznie różnych) elementów
ma dokładnie jedno przedstawienie w postaci sumy dwóch (niekoniecznie różnych) elementów 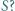
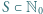 o tej własności, że każdy element niepustego zbioru
o tej własności, że każdy element niepustego zbioru 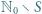 ma dokładnie jedno przedstawienie w postaci sumy dwóch (niekoniecznie różnych) elementów
ma dokładnie jedno przedstawienie w postaci sumy dwóch (niekoniecznie różnych) elementów 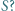
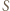 istnieje. Aby liczby 0 oraz
istnieje. Aby liczby 0 oraz 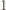 miały przedstawienia w postaci odpowiednich sum, musimy mieć
miały przedstawienia w postaci odpowiednich sum, musimy mieć 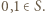 Gdyby
Gdyby 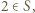 to mielibyśmy dwa przedstawienia tej liczby jako sumy elementów
to mielibyśmy dwa przedstawienia tej liczby jako sumy elementów 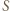 :
: 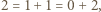 a zatem
a zatem 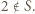 Podobne rozważania prowadzą kolejno do wniosków, że
Podobne rozważania prowadzą kolejno do wniosków, że 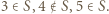 Ale
Ale 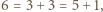 sprzeczność.
sprzeczność.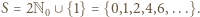 Wówczas każda liczba nieparzysta większa od
Wówczas każda liczba nieparzysta większa od 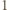 (czyli każdy element zbioru
(czyli każdy element zbioru 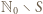 ) postaci
) postaci 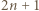 ma dokładnie jedno przedstawienie w postaci sumy dwóch elementów
ma dokładnie jedno przedstawienie w postaci sumy dwóch elementów 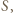 mianowicie
mianowicie 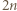 oraz
oraz