Najważniejsza nierówność na świecie»Zadanie 1
o zadaniu...
- Zadanie pochodzi z artykułu Najważniejsza nierówność na świecie
- Publikacja w Delcie: maj 2019
- Publikacja elektroniczna: 30 kwietnia 2019
- Artykuł źródłowy w wersji do druku [application/pdf]: (350 KB)
Udowodnić, że dla liczb dodatnich 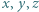 prawdziwa jest nierówność
prawdziwa jest nierówność

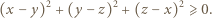

 i
i 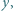 niebędących jednocześnie zerami.
niebędących jednocześnie zerami.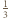 oraz
oraz  Rozwiązanie ułatwia spostrzeżenie, że szacowany ułamek ma dodatni licznik i mianownik, bo
Rozwiązanie ułatwia spostrzeżenie, że szacowany ułamek ma dodatni licznik i mianownik, bo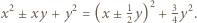
 zachodzi nierówność
zachodzi nierówność
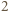 i przeniesieniu wszystkich wyrazów na lewą stronę nierówności otrzymamy
i przeniesieniu wszystkich wyrazów na lewą stronę nierówności otrzymamy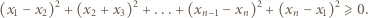

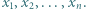
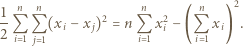
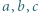 jest równa
jest równa 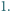 Udowodnić, że
Udowodnić, że
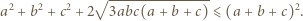
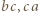 i
i 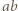 ułatwia dalsze rachunki.
ułatwia dalsze rachunki.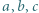 spełniają równość
spełniają równość 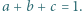 Wykazać, że
Wykazać, że
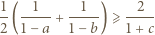
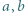 i
i  zachodzi nierówność
zachodzi nierówność
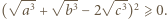
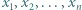 będą liczbami dodatnimi. Przyjmijmy
będą liczbami dodatnimi. Przyjmijmy 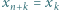 dla całkowitych
dla całkowitych 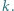 Dowieść, że prawdziwa jest co najmniej jedna z nierówności:
Dowieść, że prawdziwa jest co najmniej jedna z nierówności:
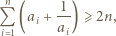
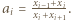
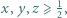 spełniających warunek
spełniających warunek 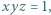 zachodzi nierówność
zachodzi nierówność
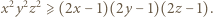
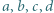 spełniają nierówność
spełniają nierówność
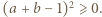
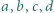 zachodzi nierówność
zachodzi nierówność
![x ,x ,...,x ∈ [−1,1] 1 2 n](/math/temat/matematyka/analiza/zadania/2019/04/29/zm-19_05-kpm-12/1x-e242253ed078688e97a06aead3aec19a78e70a97-im-2C,6B,73-FF,FF,FF.gif) spełniają warunek
spełniają warunek 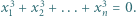 Dowieść, że
Dowieść, że
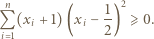
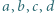 zachodzi nierówność
zachodzi nierówność

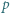 będzie nieparzystą liczbą pierwszą oraz
będzie nieparzystą liczbą pierwszą oraz 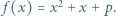 Przypuśćmy, że liczba
Przypuśćmy, że liczba 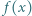 jest pierwsza dla każdej dodatniej liczby całkowitej
jest pierwsza dla każdej dodatniej liczby całkowitej  nie większej od
nie większej od 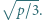 Wykazać, że liczba
Wykazać, że liczba 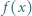 jest pierwsza dla każdej dodatniej liczby całkowitej
jest pierwsza dla każdej dodatniej liczby całkowitej 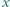 nie większej od
nie większej od 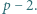
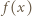 jest liczbą złożoną dla pewnego
jest liczbą złożoną dla pewnego 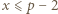 i oznaczmy przez
i oznaczmy przez  najmniejszą taką dodatnią liczbę całkowitą, że
najmniejszą taką dodatnią liczbę całkowitą, że 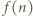 jest liczbą złożoną. Z założeń zadania wynika, że
jest liczbą złożoną. Z założeń zadania wynika, że 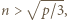 czyli
czyli 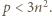
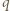 najmniejszy dzielnik pierwszy liczby
najmniejszy dzielnik pierwszy liczby 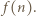 Zauważmy, że
Zauważmy, że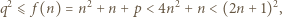
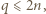 czyli istnieje liczba całkowita
czyli istnieje liczba całkowita 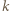 o tej własności, że
o tej własności, że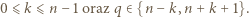
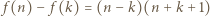
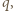 więc skoro
więc skoro 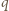 dzieli
dzieli 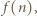 to również
to również 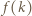 jest liczbą podzielną przez
jest liczbą podzielną przez 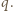 Pozostaje zauważyć, że
Pozostaje zauważyć, że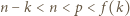
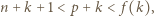
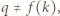 a co za tym idzie -
a co za tym idzie - 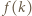 jest liczbą złożoną. Jednak
jest liczbą złożoną. Jednak 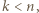 więc stoi to w sprzeczności z wyborem liczby
więc stoi to w sprzeczności z wyborem liczby 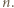
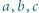 spełniają równości
spełniają równości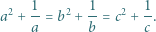
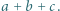
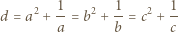
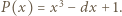 Skoro
Skoro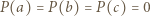
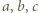 są różne, to są one różnymi pierwiastkami wielomianu
są różne, to są one różnymi pierwiastkami wielomianu 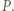 Stąd na mocy wzorów Viéte'a uzyskujemy
Stąd na mocy wzorów Viéte'a uzyskujemy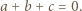
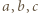 spełniające założenia zadania rzeczywiście istnieją, np.
spełniające założenia zadania rzeczywiście istnieją, np.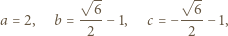
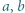 spełniają równość
spełniają równość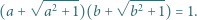
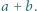
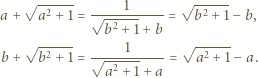
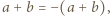 czyli
czyli 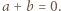
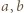 spełniające założenia zadania rzeczywiście istnieją (np.
spełniające założenia zadania rzeczywiście istnieją (np. 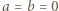 ), więc znaleziona wartość 0 istotnie jest osiągalna.
), więc znaleziona wartość 0 istotnie jest osiągalna.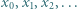 jest określony wzorami:
jest określony wzorami: 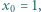

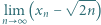 lub wykazać, że ta granica nie istnieje.
lub wykazać, że ta granica nie istnieje.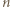 literką
literką 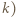 i dostajemy równoważną zależność
i dostajemy równoważną zależność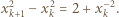
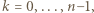 otrzymując
otrzymując
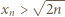 (dla
(dla 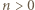 ), i wobec tego
), i wobec tego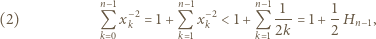
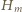 oznacza sumę odwrotności liczb naturalnych od 1 do
oznacza sumę odwrotności liczb naturalnych od 1 do  Zależności (1) i (2) dają oszacowanie
Zależności (1) i (2) dają oszacowanie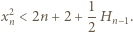
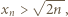 mamy stąd
mamy stąd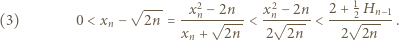
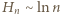 ; albo - bardziej elementarnie - z nierówności
; albo - bardziej elementarnie - z nierówności 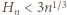 (nietrudnej do wykazania przez indukcję). Dwustronne oszacowanie (3) pokazuje, że
(nietrudnej do wykazania przez indukcję). Dwustronne oszacowanie (3) pokazuje, że 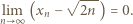
 jest nieparzysta. Dowieść, że zbiór
jest nieparzysta. Dowieść, że zbiór 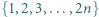 ma tyle samo
ma tyle samo  -elementowych podzbiorów o parzystej sumie elementów, co
-elementowych podzbiorów o parzystej sumie elementów, co 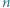 -elementowych podzbiorów o nieparzystej sumie elementów.
-elementowych podzbiorów o nieparzystej sumie elementów.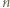 -elementowy o parzystej sumie elementów można sparować z jego dopełnieniem w zbiorze
-elementowy o parzystej sumie elementów można sparować z jego dopełnieniem w zbiorze 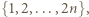 które również ma
które również ma 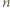 elementów, a ich suma jest nieparzysta.
elementów, a ich suma jest nieparzysta. -kąta wypukłego nie przecinają się w jednym punkcie. Ile jest punktów przecięcia się przekątnych wewnątrz tego wielokąta?
-kąta wypukłego nie przecinają się w jednym punkcie. Ile jest punktów przecięcia się przekątnych wewnątrz tego wielokąta?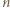 -kąta należy dobrać w parę z czwórką (nieuporządkowaną) wierzchołków
-kąta należy dobrać w parę z czwórką (nieuporządkowaną) wierzchołków  -kąta, które są końcami tych przekątnych.
-kąta, które są końcami tych przekątnych.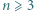 punktów niebieskich leży na wspólnym okręgu. Których wielokątów jest więcej: posiadających wyłącznie niebieskie wierzchołki, czy tych, które posiadają jeden czerwony wierzchołek, a pozostałe niebieskie?
punktów niebieskich leży na wspólnym okręgu. Których wielokątów jest więcej: posiadających wyłącznie niebieskie wierzchołki, czy tych, które posiadają jeden czerwony wierzchołek, a pozostałe niebieskie?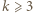 każdy
każdy 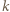 -kąt o niebieskich wierzchołkach parujemy z
-kąt o niebieskich wierzchołkach parujemy z 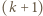 -kątem o jednym wierzchołkiem czerwonym, powstającym przez dołączenie tego wierzchołka. Bez pary pozostaną jedynie trójkąty z czerwonym wierzchołkiem, zatem wielokątów z czerwonym wierzchołkiem jest więcej.
-kątem o jednym wierzchołkiem czerwonym, powstającym przez dołączenie tego wierzchołka. Bez pary pozostaną jedynie trójkąty z czerwonym wierzchołkiem, zatem wielokątów z czerwonym wierzchołkiem jest więcej.