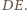Dla ustalonego, skończonego zbioru punktów na płaszczyźnie wyrażenie
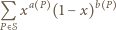
jest wielomianem zmiennej 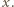 Aby wykazać, że jest to wielomian stale równy
Aby wykazać, że jest to wielomian stale równy 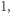 wystarczy sprawdzić, że żądana równość zachodzi dla liczb
wystarczy sprawdzić, że żądana równość zachodzi dla liczb 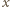 w przedziale
w przedziale 
Rozważmy losowe kolorowanie każdego z danych punktów na biało lub czarno. Załóżmy przy tym, że dowolny punkt malujemy na biało z prawdopodobieństwem 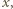 na czarno z prawdopodobieństwem
na czarno z prawdopodobieństwem 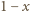 oraz że wszystkie losowania odbywają się niezależnie. Zauważmy, że wówczas dla ustalonego wielokąta
oraz że wszystkie losowania odbywają się niezależnie. Zauważmy, że wówczas dla ustalonego wielokąta 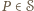 liczba
liczba 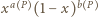 jest prawdopodobieństwem zdarzenia, w którym wszystkie wierzchołki
jest prawdopodobieństwem zdarzenia, w którym wszystkie wierzchołki 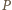 zostały pomalowane na biało, a punkty leżące na zewnątrz
zostały pomalowane na biało, a punkty leżące na zewnątrz 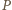 na czarno. Co więcej, dla dwóch różnych wielokątów
na czarno. Co więcej, dla dwóch różnych wielokątów 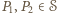 tego typu zdarzenia wykluczają się wzajemnie. Dla dowolnych dwóch różnych wielokątów wypukłych istnieje bowiem wierzchołek jednego z nich, który nie należy do drugiego. Gdyby opisane zdarzenia nie były rozłączne, to wierzchołek ten musiałby być pomalowany na dwa kolory, co jest, oczywiście, niemożliwe.
tego typu zdarzenia wykluczają się wzajemnie. Dla dowolnych dwóch różnych wielokątów wypukłych istnieje bowiem wierzchołek jednego z nich, który nie należy do drugiego. Gdyby opisane zdarzenia nie były rozłączne, to wierzchołek ten musiałby być pomalowany na dwa kolory, co jest, oczywiście, niemożliwe.
Suma
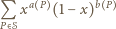
jest w tej sytuacji prawdopodobieństwem zdarzenia, w którym wierzchołki jednego z wielokątów 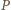 ze zbioru
ze zbioru 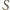 zostały pomalowane na biało, zaś punkty leżące na zewnątrz
zostały pomalowane na biało, zaś punkty leżące na zewnątrz 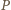 na czarno. Do rozwiązania zadania wystarczy więc stwierdzić, że jest to zdarzenie pewne - co oznacza, że w dowolnym pokolorowaniu taki wielokąt istnieje.
na czarno. Do rozwiązania zadania wystarczy więc stwierdzić, że jest to zdarzenie pewne - co oznacza, że w dowolnym pokolorowaniu taki wielokąt istnieje.
Szukanym wielokątem jest wielokąt 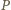 będący otoczką wypukłą białych punktów - czyli najmniejszym wielokątem wypukłym, który zawiera punkty białe (w przypadku gdy liczba punktów białych jest równa
będący otoczką wypukłą białych punktów - czyli najmniejszym wielokątem wypukłym, który zawiera punkty białe (w przypadku gdy liczba punktów białych jest równa 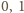 lub
lub 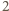 ich otoczką wypukłą jest odpowiednio zbiór pusty, punkt i odcinek). Jego wierzchołki są koloru białego, a każdy inny punkt biały znajduje się w jego wnętrzu.
ich otoczką wypukłą jest odpowiednio zbiór pusty, punkt i odcinek). Jego wierzchołki są koloru białego, a każdy inny punkt biały znajduje się w jego wnętrzu.
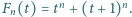 Udowodnić, że istnieje nieskończenie wiele liczb całkowitych
Udowodnić, że istnieje nieskończenie wiele liczb całkowitych 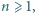 dla których równanie
dla których równanie 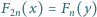 nie ma rozwiązań w liczbach całkowitych
nie ma rozwiązań w liczbach całkowitych 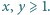
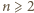 równanie może mieć w liczbach całkowitych
równanie może mieć w liczbach całkowitych 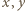 co najwyżej skończenie wiele rozwiązań (autor: Marcin Mazur); zaś w rocznym omówieniu (Delta 2/1992) pozostało otwarte pytanie, czy to równanie w ogóle ma rozwiązania poza trywialnymi
co najwyżej skończenie wiele rozwiązań (autor: Marcin Mazur); zaś w rocznym omówieniu (Delta 2/1992) pozostało otwarte pytanie, czy to równanie w ogóle ma rozwiązania poza trywialnymi 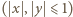 ; obecna propozycja to mały krok w kierunku próby badania tego problemu.
; obecna propozycja to mały krok w kierunku próby badania tego problemu.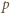 jest nieparzystą liczbą pierwszą, równanie
jest nieparzystą liczbą pierwszą, równanie 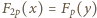 nie ma rozwiązań w liczbach całkowitych dodatnich.
nie ma rozwiązań w liczbach całkowitych dodatnich.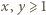 jest rozwiązaniem. Zgodnie z małym twierdzeniem Fermata,
jest rozwiązaniem. Zgodnie z małym twierdzeniem Fermata,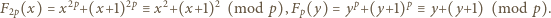
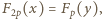 to
to 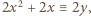 czyli
czyli 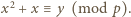
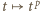 (w zbiorze liczb dodatnich) wynika nierówność
(w zbiorze liczb dodatnich) wynika nierówność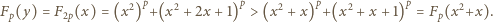
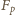 jest rosnąca; stąd
jest rosnąca; stąd 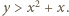 Skoro zaś
Skoro zaś 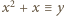 (mod
(mod 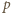 ), widzimy, że
), widzimy, że 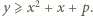 A zatem
A zatem 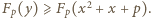 Aby uzyskać oczekiwaną sprzeczność, wystarczy wykazać, że
Aby uzyskać oczekiwaną sprzeczność, wystarczy wykazać, że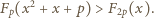
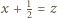 ; wtedy
; wtedy 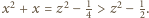 Ponownie korzystając z wypukłości funkcji
Ponownie korzystając z wypukłości funkcji 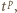 mamy nierówność
mamy nierówność 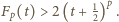 Wobec tego
Wobec tego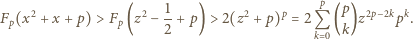
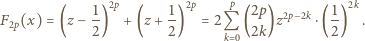
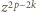 jest nie mniejszy niż analogiczny współczynnik w wyrażeniu (3); czyli, że
jest nie mniejszy niż analogiczny współczynnik w wyrażeniu (3); czyli, że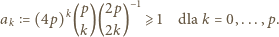
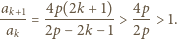
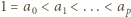 ; oszacowanie (4) gotowe, dowód zakończony.
; oszacowanie (4) gotowe, dowód zakończony. będzie ustaloną dodatnią liczbą nieparzystą. Wyznaczyć największą możliwą liczność zbioru złożonego z liczb całkowitych dodatnich, mniejszych od
będzie ustaloną dodatnią liczbą nieparzystą. Wyznaczyć największą możliwą liczność zbioru złożonego z liczb całkowitych dodatnich, mniejszych od  w którym każde dwa różne elementy mają i różnicę, i sumę różną od
w którym każde dwa różne elementy mają i różnicę, i sumę różną od 
 jest nieparzysta, zatem zbiór wszystkich liczb parzystych, mniejszych od
jest nieparzysta, zatem zbiór wszystkich liczb parzystych, mniejszych od  ma własność, o którą chodzi. Jest ich
ma własność, o którą chodzi. Jest ich 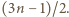 Wykażemy, że jest to największa możliwa liczność.
Wykażemy, że jest to największa możliwa liczność.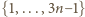 na rozłączne pary:
na rozłączne pary: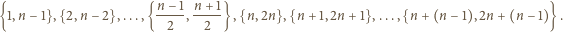
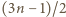 par liczb. Zbiór o większej liczności (zawarty w
par liczb. Zbiór o większej liczności (zawarty w 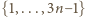 ) musi zawierać jedną z wymienionych par. Ale w każdej parze albo suma, albo różnica elementów jest równa
) musi zawierać jedną z wymienionych par. Ale w każdej parze albo suma, albo różnica elementów jest równa 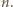 Stąd nasza teza.
Stąd nasza teza.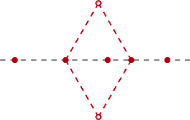
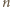 swoich ruchach Maja maluje na kolorowo
swoich ruchach Maja maluje na kolorowo 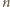 punktów z jednej prostej. Każdą parę takich kolorowych punktów można na dwa sposoby uzupełnić do trójkąta równobocznego, par punktów spośród
punktów z jednej prostej. Każdą parę takich kolorowych punktów można na dwa sposoby uzupełnić do trójkąta równobocznego, par punktów spośród  jest
jest 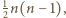 więc łącznie po
więc łącznie po 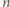 ruchach na płaszczyźnie jest
ruchach na płaszczyźnie jest 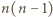 takich punktów, że pomalowanie dowolnego z nich na kolorowo da Mai zwycięstwo.
takich punktów, że pomalowanie dowolnego z nich na kolorowo da Mai zwycięstwo.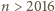 mamy
mamy 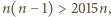 zatem Gucio nie może w swoich początkowych
zatem Gucio nie może w swoich początkowych 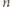 ruchach wszystkich opisanych powyżej punktów pomalować na czarno i Maja może wygrać w ruchu numer
ruchach wszystkich opisanych powyżej punktów pomalować na czarno i Maja może wygrać w ruchu numer 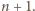
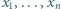 będą liczbami rzeczywistymi dodatnimi, przy czym
będą liczbami rzeczywistymi dodatnimi, przy czym 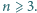 Dla wygody przyjmijmy dodatkowo, że
Dla wygody przyjmijmy dodatkowo, że 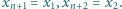 Udowodnić, że
Udowodnić, że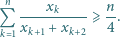
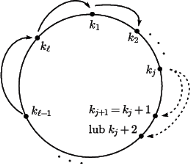
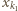 oznacza największą z liczb
oznacza największą z liczb 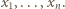 Popatrzmy na wyraz
Popatrzmy na wyraz 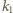 naszej sumy:
naszej sumy: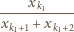
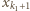 lub
lub 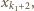 przez
przez 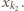 Popatrzmy teraz na wyraz
Popatrzmy teraz na wyraz 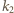 naszej sumy:
naszej sumy: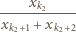
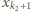 lub
lub 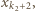 przez
przez 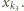 Kontynuując to postępowanie, otrzymujemy ciąg indeksów
Kontynuując to postępowanie, otrzymujemy ciąg indeksów 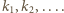
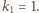 Z definicji mamy
Z definicji mamy 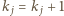 lub
lub 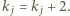 Zatem po pewnej liczbie kroków po raz pierwszy otrzymamy
Zatem po pewnej liczbie kroków po raz pierwszy otrzymamy 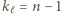 lub
lub 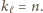 Ponadto
Ponadto 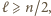 bo w każdym kroku przesuwamy się o co najwyżej dwa. Zauważmy też, że
bo w każdym kroku przesuwamy się o co najwyżej dwa. Zauważmy też, że 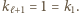
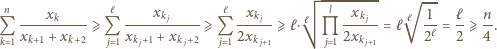

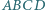 boki
boki 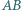 i
i 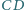 są równoległe oraz
są równoległe oraz 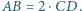 Punkt
Punkt 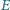 jest środkiem boku
jest środkiem boku 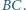 Udowodnić, że jeśli
Udowodnić, że jeśli 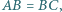 to w czworokąt
to w czworokąt 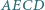 można wpisać okrąg.
można wpisać okrąg.
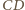 punkt
punkt 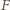 w taki sposób, aby czworokąt
w taki sposób, aby czworokąt 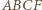 był równoległobokiem.
był równoległobokiem.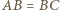 możemy wywnioskować, że
możemy wywnioskować, że 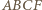 jest rombem. Ponadto, skoro
jest rombem. Ponadto, skoro 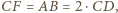 to punkt
to punkt 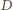 jest środkiem boku
jest środkiem boku 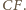 Ponieważ punkt
Ponieważ punkt 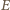 jest środkiem boku
jest środkiem boku 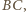 więc punkty
więc punkty 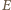 i
i 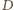 są symetryczne względem prostej
są symetryczne względem prostej 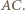 Oznacza to, że czworokąt
Oznacza to, że czworokąt 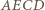 jest deltoidem, zatem w szczególności można w niego wpisać okrąg.
jest deltoidem, zatem w szczególności można w niego wpisać okrąg.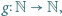 spełniającej warunek
spełniającej warunek 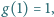 istnieje funkcja
istnieje funkcja 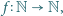 spełniająca warunki
spełniająca warunki 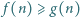 dla
dla 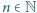 oraz
oraz 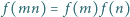 dla każdej pary liczb względnie pierwszych
dla każdej pary liczb względnie pierwszych 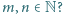 (
( 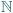 to zbiór wszystkich liczb całkowitych dodatnich).
to zbiór wszystkich liczb całkowitych dodatnich).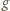 łatwo wskazać funkcję
łatwo wskazać funkcję 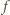 o wymaganych własnościach. Niech
o wymaganych własnościach. Niech 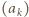 będzie rosnącym ciągiem wszystkich potęg liczb pierwszych:
będzie rosnącym ciągiem wszystkich potęg liczb pierwszych: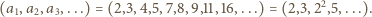
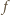 (o własności
(o własności 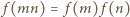 gdy
gdy 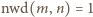 ) jest wyznaczona przez ciąg wartości
) jest wyznaczona przez ciąg wartości 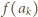 ; zaś podany warunek multyplikatywności nie stawia na owe wartości żadnych ograniczeń. Wobec tego konstruujemy taki ciąg indukcyjnie. Niech
; zaś podany warunek multyplikatywności nie stawia na owe wartości żadnych ograniczeń. Wobec tego konstruujemy taki ciąg indukcyjnie. Niech 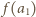 będzie dowolną liczbą naturalną większą od
będzie dowolną liczbą naturalną większą od 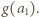
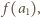 …,
…, 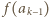 zostały już określone. Patrzymy na zbiór wszystkich liczb postaci
zostały już określone. Patrzymy na zbiór wszystkich liczb postaci 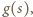 gdzie
gdzie  jest iloczynem różnych liczb ze zbioru
jest iloczynem różnych liczb ze zbioru 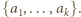 Określamy
Określamy 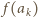 jako dowolną liczbę naturalną większą od wszystkich takich liczb
jako dowolną liczbę naturalną większą od wszystkich takich liczb 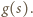
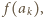 wraz z warunkiem multyplikatywności, jednoznacznie generuje funkcję
wraz z warunkiem multyplikatywności, jednoznacznie generuje funkcję 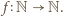 Spełnia ona także pozostały z zadanych warunków; jeśli bowiem liczba
Spełnia ona także pozostały z zadanych warunków; jeśli bowiem liczba 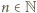 zostanie zapisana jako iloczyn
zostanie zapisana jako iloczyn 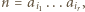 gdzie
gdzie 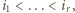 wówczas
wówczas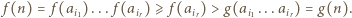
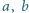 i
i  różne od zera, że liczba
różne od zera, że liczba 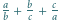 jest całkowita. Wykazać, że iloczyn
jest całkowita. Wykazać, że iloczyn 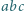 jest sześcianem liczby całkowitej.
jest sześcianem liczby całkowitej.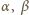 i
i 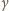 są niepodzielne przez liczbę pierwszą
są niepodzielne przez liczbę pierwszą 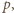 oraz że dla pewnej trójki liczb całkowitych nieujemnych
oraz że dla pewnej trójki liczb całkowitych nieujemnych 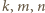 zachodzą równości
zachodzą równości 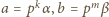 i
i 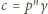 (w dalszym ciągu myślę, że zadanie nie jest trudne). Aby wykazać, że iloczyn
(w dalszym ciągu myślę, że zadanie nie jest trudne). Aby wykazać, że iloczyn 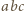 jest sześcianem pewnej liczby całkowitej, wystarczy przecież wykazać, iż każdy czynnik pierwszy występuje w rozkładzie tej liczby z wykładnikiem podzielnym przez
jest sześcianem pewnej liczby całkowitej, wystarczy przecież wykazać, iż każdy czynnik pierwszy występuje w rozkładzie tej liczby z wykładnikiem podzielnym przez 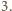 Mamy
Mamy 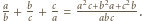 Mianownik tego ułamka jest podzielny przez liczbę
Mianownik tego ułamka jest podzielny przez liczbę 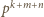 i niepodzielny przez
i niepodzielny przez 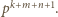 Zastąpienie uporządkowanej trójki liczb
Zastąpienie uporządkowanej trójki liczb 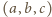 trójką
trójką 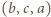 lub
lub 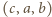 powoduje, że liczba
powoduje, że liczba 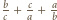 lub
lub 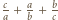 - więc ta z treści zadania - ma być całkowita (trójka
- więc ta z treści zadania - ma być całkowita (trójka 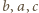 to jednak coś innego, bo na ogół
to jednak coś innego, bo na ogół 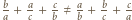 ). Można więc założyć, że
). Można więc założyć, że 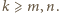 Mamy
Mamy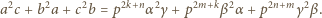
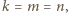 to
to 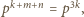 więc
więc 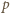 występuje w rozkładzie iloczynu
występuje w rozkładzie iloczynu 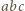 na czynniki pierwsze z wykładnikiem
na czynniki pierwsze z wykładnikiem 
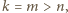 to
to 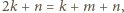
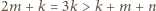 i
i 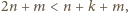 więc dwa z trzech składników licznika dzielą się przez
więc dwa z trzech składników licznika dzielą się przez 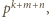 a trzeci nie, co oznacza, że liczba
a trzeci nie, co oznacza, że liczba 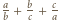 nie jest całkowita, wbrew założeniu.
nie jest całkowita, wbrew założeniu.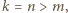 to
to 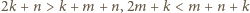 i
i 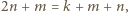 więc znów liczba
więc znów liczba 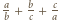 nie jest całkowita.
nie jest całkowita.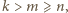 to
to 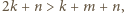
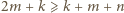 i
i 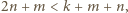 więc znów liczba
więc znów liczba 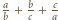 nie jest całkowita.
nie jest całkowita.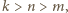 to
to 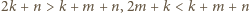 i
i 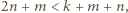 to teraz dwa składniki nie dzielą się przez
to teraz dwa składniki nie dzielą się przez 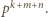 Ich suma może dzielić się przez
Ich suma może dzielić się przez 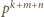 tylko wtedy, gdy
tylko wtedy, gdy 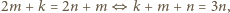 więc w tym wypadku liczba
więc w tym wypadku liczba 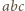 jest podzielna przez
jest podzielna przez 
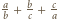 jest całkowita, to liczba pierwsza
jest całkowita, to liczba pierwsza 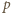 wchodzi w rozkład liczby
wchodzi w rozkład liczby 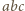 na czynniki pierwsze z wykładnikiem podzielnym przez
na czynniki pierwsze z wykładnikiem podzielnym przez 
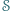 oznacza zbiór wszystkich wielokątów wypukłych o wierzchołkach w tym zbiorze (jako wielokąty wypukłe traktujemy również zbiór pusty, pojedyncze punkty oraz odcinki). Dla dowolnego wielokąta
oznacza zbiór wszystkich wielokątów wypukłych o wierzchołkach w tym zbiorze (jako wielokąty wypukłe traktujemy również zbiór pusty, pojedyncze punkty oraz odcinki). Dla dowolnego wielokąta 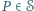 przez
przez 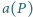 i
i 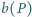 oznaczamy odpowiednio liczbę punktów z danego zbioru, które leżą na obwodzie i na zewnątrz wielokąta
oznaczamy odpowiednio liczbę punktów z danego zbioru, które leżą na obwodzie i na zewnątrz wielokąta 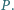 Wykazać, że dla każdej liczby rzeczywistej
Wykazać, że dla każdej liczby rzeczywistej  zachodzi równość
zachodzi równość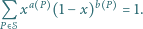
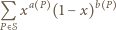
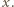 Aby wykazać, że jest to wielomian stale równy
Aby wykazać, że jest to wielomian stale równy 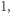 wystarczy sprawdzić, że żądana równość zachodzi dla liczb
wystarczy sprawdzić, że żądana równość zachodzi dla liczb 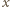 w przedziale
w przedziale 
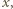 na czarno z prawdopodobieństwem
na czarno z prawdopodobieństwem 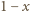 oraz że wszystkie losowania odbywają się niezależnie. Zauważmy, że wówczas dla ustalonego wielokąta
oraz że wszystkie losowania odbywają się niezależnie. Zauważmy, że wówczas dla ustalonego wielokąta 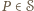 liczba
liczba 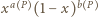 jest prawdopodobieństwem zdarzenia, w którym wszystkie wierzchołki
jest prawdopodobieństwem zdarzenia, w którym wszystkie wierzchołki 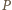 zostały pomalowane na biało, a punkty leżące na zewnątrz
zostały pomalowane na biało, a punkty leżące na zewnątrz 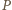 na czarno. Co więcej, dla dwóch różnych wielokątów
na czarno. Co więcej, dla dwóch różnych wielokątów 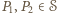 tego typu zdarzenia wykluczają się wzajemnie. Dla dowolnych dwóch różnych wielokątów wypukłych istnieje bowiem wierzchołek jednego z nich, który nie należy do drugiego. Gdyby opisane zdarzenia nie były rozłączne, to wierzchołek ten musiałby być pomalowany na dwa kolory, co jest, oczywiście, niemożliwe.
tego typu zdarzenia wykluczają się wzajemnie. Dla dowolnych dwóch różnych wielokątów wypukłych istnieje bowiem wierzchołek jednego z nich, który nie należy do drugiego. Gdyby opisane zdarzenia nie były rozłączne, to wierzchołek ten musiałby być pomalowany na dwa kolory, co jest, oczywiście, niemożliwe.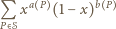
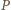 ze zbioru
ze zbioru 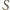 zostały pomalowane na biało, zaś punkty leżące na zewnątrz
zostały pomalowane na biało, zaś punkty leżące na zewnątrz 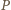 na czarno. Do rozwiązania zadania wystarczy więc stwierdzić, że jest to zdarzenie pewne - co oznacza, że w dowolnym pokolorowaniu taki wielokąt istnieje.
na czarno. Do rozwiązania zadania wystarczy więc stwierdzić, że jest to zdarzenie pewne - co oznacza, że w dowolnym pokolorowaniu taki wielokąt istnieje.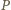 będący otoczką wypukłą białych punktów - czyli najmniejszym wielokątem wypukłym, który zawiera punkty białe (w przypadku gdy liczba punktów białych jest równa
będący otoczką wypukłą białych punktów - czyli najmniejszym wielokątem wypukłym, który zawiera punkty białe (w przypadku gdy liczba punktów białych jest równa 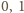 lub
lub 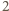 ich otoczką wypukłą jest odpowiednio zbiór pusty, punkt i odcinek). Jego wierzchołki są koloru białego, a każdy inny punkt biały znajduje się w jego wnętrzu.
ich otoczką wypukłą jest odpowiednio zbiór pusty, punkt i odcinek). Jego wierzchołki są koloru białego, a każdy inny punkt biały znajduje się w jego wnętrzu.

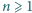 znaleźć wartość sumy
znaleźć wartość sumy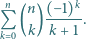
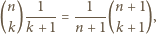
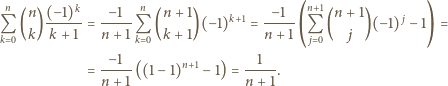
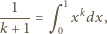
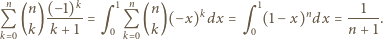

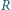 i
i  są styczne zewnętrznie. Poprowadzono ich wspólną styczną i w obszar ograniczony przez nią i okręgi wpisano okrąg. Ile wynosi jego promień?
są styczne zewnętrznie. Poprowadzono ich wspólną styczną i w obszar ograniczony przez nią i okręgi wpisano okrąg. Ile wynosi jego promień?
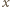 oznacza szukany promień. Jeden z trójkątów prostokątnych widocznych na rysunku ma przeciwprostokątną będącą sumą promieni o długościach
oznacza szukany promień. Jeden z trójkątów prostokątnych widocznych na rysunku ma przeciwprostokątną będącą sumą promieni o długościach 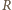 i
i  oraz przyprostokątną o długości
oraz przyprostokątną o długości 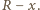 Z twierdzenia Pitagorasa otrzymujemy, że długość drugiej przyprostokątnej, a więc również długość odcinka pomiędzy odpowiednimi punktami styczności jest równa
Z twierdzenia Pitagorasa otrzymujemy, że długość drugiej przyprostokątnej, a więc również długość odcinka pomiędzy odpowiednimi punktami styczności jest równa 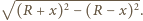
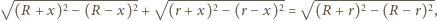
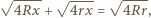
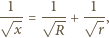
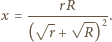

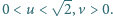
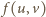 to kwadrat odległości między punktami
to kwadrat odległości między punktami 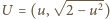 oraz
oraz 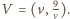
 zadanym równaniem
zadanym równaniem 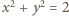 (a dokładniej na jego części znajdującej się w pierwszej ćwiartce układu współrzędnych), a drugi na gałęzi hiperboli
(a dokładniej na jego części znajdującej się w pierwszej ćwiartce układu współrzędnych), a drugi na gałęzi hiperboli 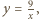 dla
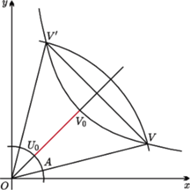
dla 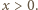 Aby znaleźć najmniejszą wartość funkcji
Aby znaleźć najmniejszą wartość funkcji 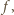 wystarczy znaleźć odległość okręgu
wystarczy znaleźć odległość okręgu 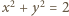 od hiperboli
od hiperboli 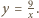 Niech
Niech 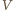 będzie wybranym punktem na hiperboli, a punkt
będzie wybranym punktem na hiperboli, a punkt 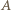 punktem przecięcia
punktem przecięcia  z odcinkiem
z odcinkiem 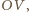 gdzie
gdzie 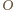 jest środkiem układu współrzędnych (patrz rysunek). Odległość punktu
jest środkiem układu współrzędnych (patrz rysunek). Odległość punktu 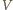 od
od  jest równa długości odcinka
jest równa długości odcinka 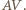 Niech punkt
Niech punkt 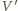 będzie symetryczny do
będzie symetryczny do 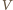 względem prostej
względem prostej 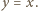 Odległość
Odległość 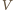 od
od  jest równa odległości
jest równa odległości 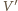 od
od 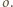 Ponadto, z wypukłości funkcji
Ponadto, z wypukłości funkcji 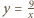 dla
dla 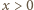 wynika, że punkt
wynika, że punkt 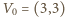 znajduje się po przeciwnej stronie prostej
znajduje się po przeciwnej stronie prostej 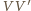 niż łuk okręgu o środku w punkcie
niż łuk okręgu o środku w punkcie 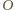 i promieniu równym długości odcinka
i promieniu równym długości odcinka 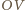 łączący punkty
łączący punkty 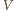 i
i 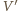 (patrz rysunek). Zatem odległość
(patrz rysunek). Zatem odległość 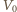 od
od  jest mniejsza niż odległość
jest mniejsza niż odległość 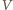 od
od 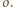 Z dowolności
Z dowolności 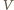 wynika, że najmniejsza wartość funkcji
wynika, że najmniejsza wartość funkcji 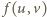 jest równa kwadratowi długości odcinka
jest równa kwadratowi długości odcinka 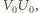 gdzie
gdzie 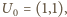 czyli
czyli 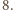
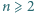 znaleźć najmniejszą wartość sumy
znaleźć najmniejszą wartość sumy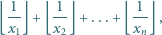
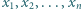 są dowolnymi liczbami rzeczywistymi dodatnimi, spełniającymi warunek
są dowolnymi liczbami rzeczywistymi dodatnimi, spełniającymi warunek 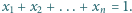
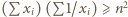 ; we wszystkich symbolach sumowania przyjmujemy
; we wszystkich symbolach sumowania przyjmujemy 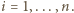 Przy warunku
Przy warunku 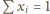 mamy więc
mamy więc 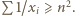 Dla każdej liczby rzeczywistej
Dla każdej liczby rzeczywistej 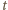 słuszne jest oszacowanie
słuszne jest oszacowanie 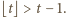 Stąd
Stąd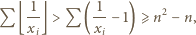
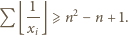
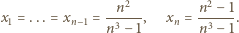
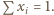 Dla
Dla 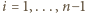 mamy przy tym
mamy przy tym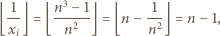
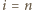 :
: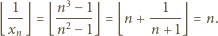
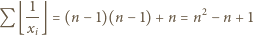
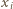 ; można dać wiele innych przykładów). Wniosek: liczba
; można dać wiele innych przykładów). Wniosek: liczba 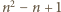 to szukane minimum.
to szukane minimum.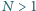 bezkwadratowa (tj. niepodzielna przez kwadrat żadnej liczby naturalnej większej od 1). Spośród wszystkich dodatnich dzielników liczby
bezkwadratowa (tj. niepodzielna przez kwadrat żadnej liczby naturalnej większej od 1). Spośród wszystkich dodatnich dzielników liczby 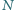 losujemy kolejno, bez zwracania, dwa dzielniki:
losujemy kolejno, bez zwracania, dwa dzielniki: 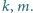 Rozważamy zdarzenia:
Rozważamy zdarzenia: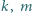 są względnie pierwsze;
są względnie pierwsze; jest podzielna przez
jest podzielna przez 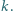
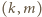 dzielników liczby
dzielników liczby 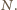 Zdarzenia
Zdarzenia 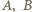 identyfikujemy z odpowiednimi podzbiorami zbioru wszystkich takich par. Gdy para
identyfikujemy z odpowiednimi podzbiorami zbioru wszystkich takich par. Gdy para 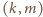 należy do
należy do 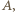 liczby
liczby 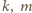 są względnie pierwszymi dzielnikami liczby
są względnie pierwszymi dzielnikami liczby 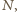 zatem także iloczyn
zatem także iloczyn 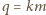 jest dzielnikiem
jest dzielnikiem 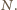 Oczywiście
Oczywiście 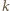 dzieli
dzieli 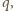 więc para
więc para 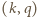 należy do
należy do 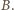
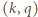 jest dowolną parą ze zbioru
jest dowolną parą ze zbioru 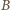 (więc
(więc 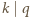 ), wtedy iloraz
), wtedy iloraz 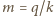 też jest dzielnikiem
też jest dzielnikiem 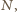 i to względnie pierwszym z
i to względnie pierwszym z 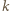 (bo gdyby
(bo gdyby 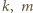 miały wspólny dzielnik
miały wspólny dzielnik 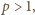 liczba
liczba 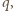 więc i
więc i 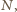 byłaby podzielna przez
byłaby podzielna przez 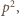 wbrew założeniu zadania). Zatem para
wbrew założeniu zadania). Zatem para 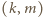 należy do
należy do 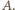
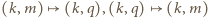 są wzajemnie odwrotne. Stąd wynika, że zbiory
są wzajemnie odwrotne. Stąd wynika, że zbiory 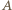 i
i 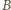 są równoliczne; zaś zdarzenia
są równoliczne; zaś zdarzenia 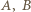 są (przy losowaniu ze zwracaniem) jednakowo prawdopodobne.
są (przy losowaniu ze zwracaniem) jednakowo prawdopodobne.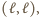 gdzie
gdzie 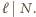 W poprzednim modelu, do zbioru
W poprzednim modelu, do zbioru 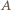 należała tylko jedna taka para
należała tylko jedna taka para 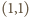 ; do
; do 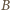 należały wszystkie. Więcej par zostało wyeliminowanych z
należały wszystkie. Więcej par zostało wyeliminowanych z 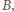 wobec czego (przy losowaniu bez zwracania) zdarzenie
wobec czego (przy losowaniu bez zwracania) zdarzenie 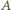 jest bardziej prawdopodobne niż
jest bardziej prawdopodobne niż 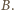
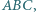 mając dany jego wierzchołek
mając dany jego wierzchołek 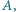 punkt
punkt 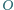 - środek okręgu opisanego i punkt
- środek okręgu opisanego i punkt 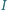 - środek okręgu wpisanego.
- środek okręgu wpisanego.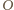 i promieniu
i promieniu 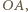
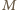 - jego punkt przecięcia z prostą
- jego punkt przecięcia z prostą 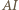 oraz okrąg o środku
oraz okrąg o środku 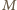 i promieniu
i promieniu 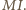 Na mocy twierdzenia
Na mocy twierdzenia 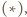 punkty przecięcia powyższych dwóch okręgów to wierzchołki
punkty przecięcia powyższych dwóch okręgów to wierzchołki 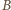 i
i 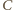 trójkąta.
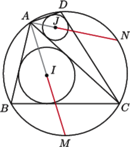
trójkąta.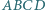 jest wpisany w okrąg
jest wpisany w okrąg 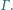 Punkt
Punkt 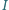 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 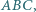 prosta
prosta 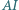 przecina okrąg
przecina okrąg 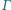 w punkcie
w punkcie 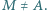 Punkt
Punkt 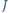 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 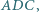 prosta
prosta 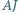 przecina okrąg
przecina okrąg 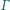 w punkcie
w punkcie 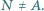 Wykaż, że jeżeli
Wykaż, że jeżeli 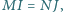 to
to 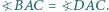
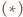 i założenia, zachodzi równość
i założenia, zachodzi równość 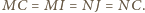 Stąd
Stąd 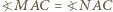 jako kąty wpisane w okrąg
jako kąty wpisane w okrąg 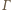 oparte na równych łukach. Wobec tego
oparte na równych łukach. Wobec tego 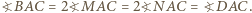
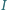 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 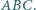 Wykaż, że okrąg opisany na trójkącie
Wykaż, że okrąg opisany na trójkącie 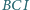 wyznacza na prostych
wyznacza na prostych 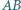 i
i 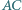 równe cięciwy.
równe cięciwy.
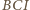 jest punkt
jest punkt 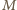 z twierdzenia
z twierdzenia 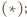 leży on na dwusiecznej kąta
leży on na dwusiecznej kąta 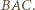 Z symetrii problemu okrąg ten wyznacza więc na ramionach kąta równe cięciwy.
Z symetrii problemu okrąg ten wyznacza więc na ramionach kąta równe cięciwy.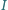 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 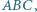 punkt
punkt 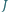 jest środkiem okręgu dopisanego do tego trójkąta. Wykaż, że środek odcinka
jest środkiem okręgu dopisanego do tego trójkąta. Wykaż, że środek odcinka 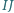 należy do okręgu opisanego na trójkącie
należy do okręgu opisanego na trójkącie 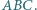
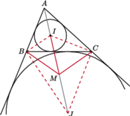
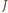 leży w kącie
leży w kącie 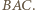 Dwusieczne kątów przyległych są prostopadłe, więc
Dwusieczne kątów przyległych są prostopadłe, więc 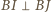 oraz
oraz 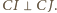 Wobec tego na czworokącie
Wobec tego na czworokącie 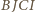 można opisać okrąg, którego środkiem jest środek
można opisać okrąg, którego środkiem jest środek 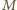 odcinka
odcinka 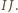 Okrąg ten jest opisany na trójkącie
Okrąg ten jest opisany na trójkącie 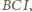 czyli
czyli 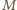 to punkt z twierdzenia
to punkt z twierdzenia 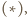 leży więc na okręgu opisanym na trójkącie
leży więc na okręgu opisanym na trójkącie 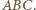
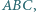 mając dane jego wierzchołki
mając dane jego wierzchołki 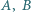 oraz promień okręgu wpisanego.
oraz promień okręgu wpisanego. jest styczny do okręgu opisanego na trójkącie
jest styczny do okręgu opisanego na trójkącie 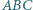 w punkcie
w punkcie 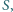 a do boków
a do boków 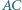 i
i 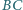 odpowiednio w punktach
odpowiednio w punktach 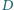 i
i 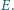 Wykaż, że jeśli
Wykaż, że jeśli 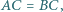 to środek okręgu wpisanego w trójkąt
to środek okręgu wpisanego w trójkąt 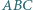 jest środkiem odcinka
jest środkiem odcinka 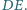
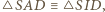 gdzie
gdzie 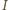 to środek odcinka
to środek odcinka