Środkowe i pola»Zadanie 4
o zadaniu...
- Zadanie pochodzi z artykułu Środkowe i pola
- Publikacja w Delcie: sierpień 2018
- Publikacja elektroniczna: 31 lipca 2018
- Artykuł źródłowy w wersji do druku [application/pdf]: (61 KB)
Wykaż, że środkowe dzielą trójkąt na sześć trójkątów o równych polach.
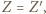 gdyż
gdyż 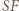 jest środkową w trójkącie
jest środkową w trójkącie 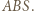 Analogicznie
Analogicznie 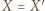 i
i 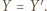 Ale także
Ale także 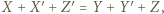 bo
bo 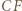 jest środkową trójkąta
jest środkową trójkąta 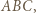 co wobec powyższego daje
co wobec powyższego daje 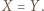 Podobnie
Podobnie 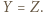
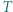 należy do wnętrza trójkąta
należy do wnętrza trójkąta 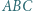 oraz
oraz 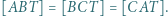 Wykaż, że
Wykaż, że 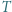 jest środkiem ciężkości trójkąta
jest środkiem ciężkości trójkąta 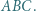
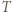 leży wewnątrz lub na brzegu trójkąta
leży wewnątrz lub na brzegu trójkąta 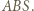 Wtedy jeśli
Wtedy jeśli 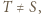 to
to 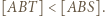 Z treści zadania wynika, że
Z treści zadania wynika, że 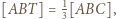 a z zadania 4 wiemy, że
a z zadania 4 wiemy, że ![|[ABS]](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-5/6x-4d0410538dd904420200c91e9bf3d520281bcf04-im-66,57,43-FF,FF,FF.gif) Stąd
Stąd 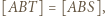 więc
więc 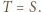
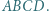 Punkty
Punkty 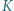 i
i 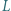 są środkami boków
są środkami boków 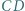 i
i 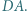 Proste
Proste 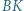 i
i 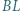 przecinają przekątną
przecinają przekątną 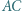 odpowiednio w punktach
odpowiednio w punktach 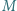 i
i 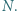 Wykaż, że
Wykaż, że ![1 ]+[BMN]+[CKM]=3[ABCD] |[ALN](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-6/11x-a985b0af3fbf2b8f27676b5a2afc831fe04a782f-im-2C,6B,73-FF,FF,FF.gif) oraz że
oraz że 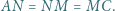
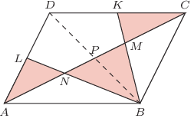
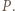 Odcinki
Odcinki 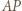 i
i 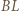 oraz
oraz 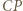 i
i 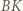 są zatem środkowymi odpowiednio w trójkątach
są zatem środkowymi odpowiednio w trójkątach 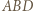 i
i 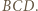 Trójkąty te mają pola równe
Trójkąty te mają pola równe ![1[ABCD] 2](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-6/8x-2283c17e109d15591b0d245c4473eb753c39dc9e-im-66,57,43-FF,FF,FF.gif) i na mocy zadania 4 ich środkowe dzielą każdy z nich na sześć trójkątów o równych polach. Stąd
i na mocy zadania 4 ich środkowe dzielą każdy z nich na sześć trójkątów o równych polach. Stąd ![12111 ]+[BMN]+[CKM]=(6+6+6)⋅2[ABCD]=3[ABCD] [ALN .](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-6/9x-2283c17e109d15591b0d245c4473eb753c39dc9e-im-66,57,43-FF,FF,FF.gif) Ponadto
Ponadto 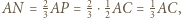 podobnie
podobnie 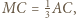 więc też
więc też 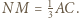
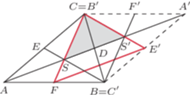
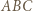 o
o 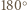 wokół punktu
wokół punktu 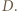 Boki trójkąta
Boki trójkąta 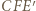 mają długości
mają długości 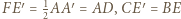 oraz
oraz 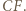
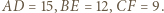 Obróćmy trójkąt
Obróćmy trójkąt 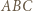 o
o 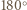 wokół punktu
wokół punktu 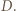 Trójkąt
Trójkąt 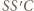 ma wówczas boki o długościach
ma wówczas boki o długościach 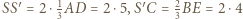 oraz
oraz 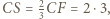 jest więc prostokątny. Stąd jego pole równe jest
jest więc prostokątny. Stąd jego pole równe jest 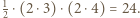 Jednocześnie na mocy zadania 4 wiemy, że pole to równe jest
Jednocześnie na mocy zadania 4 wiemy, że pole to równe jest 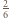 pola trójkąta
pola trójkąta 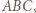 zatem
zatem ![|[ABC] .](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-8/11x-8282951b1e1d6cfb55ae221251f78463d5dae986-im-66,57,43-FF,FF,FF.gif)
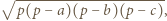
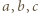 to boki,
to boki, 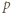 - połowa obwodu.
- połowa obwodu.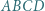 podstawa
podstawa 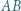 jest dwa razy dłuższa od podstawy
jest dwa razy dłuższa od podstawy 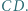 Punkt
Punkt 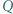 jest środkiem przekątnej
jest środkiem przekątnej 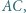 a prosta
a prosta 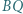 przecina bok
przecina bok 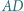 w punkcie
w punkcie 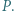 Wyznacz
Wyznacz ![[PQCD]](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-9/9x-59beed1787f722ef146fe03a4f1f01fb55efe3fb-im-2C,6B,73-FF,FF,FF.gif)
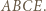
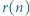 sumę
sumę  liczb będących resztami z dzielenia dodatniej liczby całkowitej
liczb będących resztami z dzielenia dodatniej liczby całkowitej 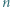 przez
przez 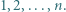 Udowodnij, że istnieje nieskończenie wiele takich
Udowodnij, że istnieje nieskończenie wiele takich 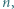 że
że 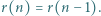
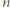 przez liczbę
przez liczbę 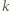 jest równa
jest równa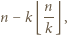
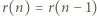 można przepisać jako
można przepisać jako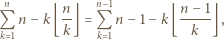
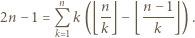
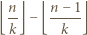
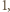 jeżeli
jeżeli 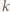 dzieli
dzieli  oraz 0 w przeciwnym przypadku. Stąd wniosek, że powyższy warunek można przepisać jako
oraz 0 w przeciwnym przypadku. Stąd wniosek, że powyższy warunek można przepisać jako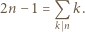
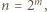 gdzie
gdzie 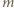 jest dodatnią liczbą całkowitą. Przykładową nieskończoną rodzinę liczb
jest dodatnią liczbą całkowitą. Przykładową nieskończoną rodzinę liczb  spełniających warunek zadania stanowią więc wszystkie potęgi dwójki.
spełniających warunek zadania stanowią więc wszystkie potęgi dwójki.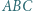 wyznacz zbiór takich punktów
wyznacz zbiór takich punktów 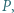 że miary kątów
że miary kątów 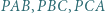 tworzą w tej właśnie kolejności ciąg arytmetyczny.
tworzą w tej właśnie kolejności ciąg arytmetyczny.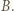
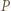 tej wysokości mamy
tej wysokości mamy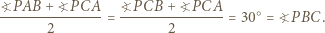
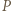 wnętrza trójkąta równobocznego
wnętrza trójkąta równobocznego 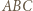 jest taki, że
jest taki, że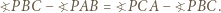
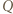 obraz punktu
obraz punktu 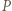 w obrocie wokół
w obrocie wokół 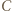 przeprowadzającym
przeprowadzającym 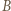 na
na 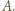 Wówczas trójkąt
Wówczas trójkąt 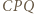 jest równoboczny.
jest równoboczny.
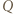 obraz punktu
obraz punktu  w obrocie wokół
w obrocie wokół 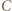 przeprowadzającym
przeprowadzającym 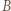 na
na 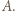 Wówczas trójkąt
Wówczas trójkąt 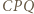 jest równoboczny.
jest równoboczny.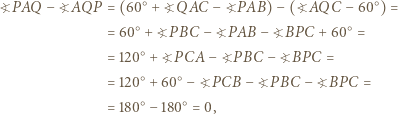
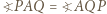 i
i 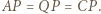 To oznacza, że punkt
To oznacza, że punkt 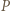 leży na symetralnej odcinka
leży na symetralnej odcinka 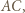 czyli na wysokości trójkąta
czyli na wysokości trójkąta 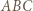 opuszczonej z
opuszczonej z 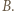
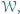 który można rozciąć płaszczyzną na dwa wielościany podobne do
który można rozciąć płaszczyzną na dwa wielościany podobne do 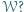
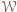 o wymiarach
o wymiarach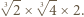
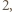 rozetniemy go na dwa przystające prostopadłościany o wymiarach
rozetniemy go na dwa przystające prostopadłościany o wymiarach 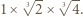 Każdy z nich jest podobny do
Każdy z nich jest podobny do 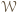 w skali
w skali 
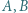 lub
lub 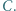 Każdy uczeń ma ustalone preferencje. W głosowaniu porównującym filmy
Każdy uczeń ma ustalone preferencje. W głosowaniu porównującym filmy 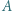 i
i 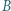 większość wybrała
większość wybrała 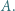 W głosowaniu pomiędzy
W głosowaniu pomiędzy 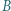 i
i 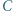 większość poparła
większość poparła 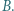 Niestety, kino wycofało film
Niestety, kino wycofało film 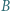 z repertuaru, pozostały do wyboru tylko
z repertuaru, pozostały do wyboru tylko 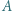 i
i 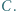 Czy większość woli
Czy większość woli 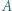 od
od 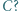
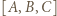 (najbardziej chcą obejrzeć
(najbardziej chcą obejrzeć 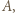 najmniej
najmniej 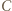 ), 10 osób uważa, że
), 10 osób uważa, że 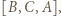 a 10, że
a 10, że 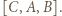 Wtedy
Wtedy 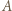 z
z 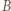 wygrywa
wygrywa 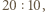 podobnie
podobnie 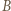 z
z 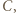 ale tak samo
ale tak samo 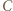 z
z 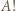
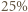 ich sumy.
ich sumy.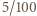 (nie zależy od losowania liści, drapania się po głowie itp.). Ponieważ ta loteria nie różni się de facto od opisanej w zadaniu, więc odpowiedź jest ta sama.
(nie zależy od losowania liści, drapania się po głowie itp.). Ponieważ ta loteria nie różni się de facto od opisanej w zadaniu, więc odpowiedź jest ta sama. listów,
listów, 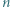 odpowiadających im zaadresowanych kopert, ale wkłada listy do kopert losowo. Dla
odpowiadających im zaadresowanych kopert, ale wkłada listy do kopert losowo. Dla 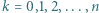 przez
przez 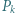 oznaczmy prawdopodobieństwo tego, że dokładnie
oznaczmy prawdopodobieństwo tego, że dokładnie 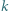 listów trafi do właściwych kopert. Wykaż, że dla
listów trafi do właściwych kopert. Wykaż, że dla 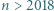 zachodzi nierówność
zachodzi nierówność
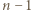 listów trafi do właściwych kopert, to
listów trafi do właściwych kopert, to 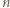 -ty też musi trafić, więc
-ty też musi trafić, więc 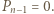
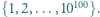 Z jakim prawdopodobieństwem nie ma ona w swym zapisie dziesiętnym żadnej cyfry 7?
Z jakim prawdopodobieństwem nie ma ona w swym zapisie dziesiętnym żadnej cyfry 7?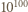 można zapisać, używając dokładnie 100 cyfr, początkowe z nich mogą być zerami (liczbę
można zapisać, używając dokładnie 100 cyfr, początkowe z nich mogą być zerami (liczbę 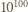 kodują same zera). Liczb bez cyfry 7 jest
kodują same zera). Liczb bez cyfry 7 jest 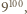 bo na każdym ze 100 miejsc zapisu dziesiętnego można wybrać dowolną spośród 9 cyfr różnych od 7. Wobec tego szukane prawdopodobieństwo równe jest
bo na każdym ze 100 miejsc zapisu dziesiętnego można wybrać dowolną spośród 9 cyfr różnych od 7. Wobec tego szukane prawdopodobieństwo równe jest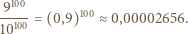
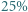 mężczyzn. Czy wynika stąd, że szczepionka ta jest skuteczniejsza dla kobiet?
mężczyzn. Czy wynika stąd, że szczepionka ta jest skuteczniejsza dla kobiet?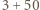 spośród 104 kobiet oraz dla
spośród 104 kobiet oraz dla 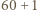 z takiej samej liczby mężczyzn.
z takiej samej liczby mężczyzn.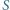 oraz nieskończenie wiele dodatnich liczb całkowitych, które można zapisać w takiej postaci.
oraz nieskończenie wiele dodatnich liczb całkowitych, które można zapisać w takiej postaci.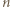 jest liczbą podzielną przez
jest liczbą podzielną przez 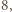 to
to  nie można zapisać w postaci sumy dwóch elementów zbioru
nie można zapisać w postaci sumy dwóch elementów zbioru 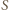 albo - w myśl tezy poprzedniego zadania - w postaci iloczynu dwóch elementów zbioru
albo - w myśl tezy poprzedniego zadania - w postaci iloczynu dwóch elementów zbioru 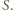 Przypuśćmy, że
Przypuśćmy, że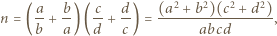
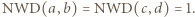 Skoro
Skoro 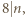 to co najmniej jeden z czynników w liczniku powyższego ułamka jest podzielny przez
to co najmniej jeden z czynników w liczniku powyższego ułamka jest podzielny przez 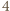 ; bez straty ogólności załóżmy, że
; bez straty ogólności załóżmy, że 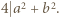 Stąd wynika, że liczby
Stąd wynika, że liczby 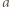 i
i 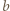 są tej samej parzystości, skąd wobec
są tej samej parzystości, skąd wobec 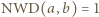 - obie są nieparzyste. Jednak wówczas
- obie są nieparzyste. Jednak wówczas 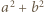 daje resztę
daje resztę 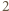 przy dzieleniu przez
przy dzieleniu przez 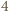 - sprzeczność.
- sprzeczność.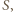 rozważymy ciąg Fibonacciego
rozważymy ciąg Fibonacciego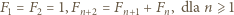
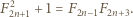
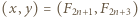 mamy więc
mamy więc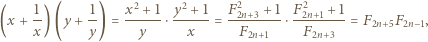
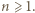 To kończy dowód, gdyż dla różnych
To kończy dowód, gdyż dla różnych 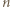 otrzymujemy różne liczby.
otrzymujemy różne liczby.