Trójmian kwadratowy»Zadanie 6
o zadaniu...
- Zadanie pochodzi z artykułu Trójmian kwadratowy
- Publikacja w Delcie: październik 2019
- Publikacja elektroniczna: 30 września 2019
- Artykuł źródłowy w wersji do druku [application/pdf]: (388 KB)
Wykorzystując funkcję kwadratową

udowodnić nierówność Cauchy'ego-Schwarza

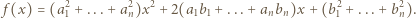
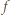 przyjmuje wyłącznie wartości nieujemne, więc
przyjmuje wyłącznie wartości nieujemne, więc 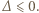 Jest to nierówność równoważna dowodzonej.
Jest to nierówność równoważna dowodzonej.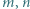 oraz
oraz 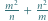 są całkowite. Udowodnić, że liczba
są całkowite. Udowodnić, że liczba 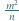 również jest całkowita.
również jest całkowita.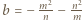 oraz
oraz 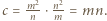 Liczby
Liczby 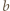 i
i  są całkowite, zaś liczby wymierne
są całkowite, zaś liczby wymierne 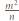 i
i 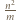 są pierwiastkami trójmianu (unormowanego)
są pierwiastkami trójmianu (unormowanego) 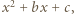 więc są całkowite.
więc są całkowite.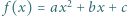 spełnia dla każdego
spełnia dla każdego ![|x∈ [−1,1]](/math/temat/matematyka/analiza/zadania/2019/09/30/zm-19_10-kpo-8/2x-74a6438c69d0f6ea8ca78cf3a770b01ff3c09138-im-2C,6B,73-FF,FF,FF.gif) nierówność
nierówność 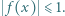 Wyznaczyć największą możliwą wartość wyrażenia
Wyznaczyć największą możliwą wartość wyrażenia 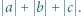
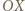 i
i 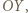 można założyć bez utraty ogólności, że
można założyć bez utraty ogólności, że 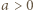 i
i 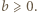 Jeśli
Jeśli 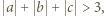 to
to 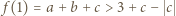 oraz
oraz 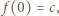 więc
więc 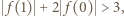 czyli
czyli 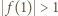 lub
lub 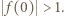 Wartość
Wartość 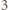 jest osiągalna, na przykład dla funkcji
jest osiągalna, na przykład dla funkcji 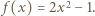
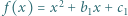 i
i 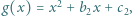 których współczynniki są rzeczywiste i spełniają warunek
których współczynniki są rzeczywiste i spełniają warunek
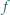 i
i 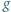 mają obydwa pierwiastki rzeczywiste, a każdy z nich ma jeden pierwiastek leżący na osi liczbowej pomiędzy pierwiastkami drugiego.
mają obydwa pierwiastki rzeczywiste, a każdy z nich ma jeden pierwiastek leżący na osi liczbowej pomiędzy pierwiastkami drugiego.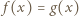 ma dokładnie jedno rozwiązanie
ma dokładnie jedno rozwiązanie 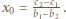 Wówczas
Wówczas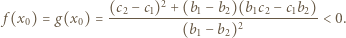
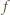 i
i 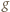 przecinają się tylko w jednym punkcie, leżącym poniżej osi
przecinają się tylko w jednym punkcie, leżącym poniżej osi 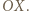 Resztę załatwia własność Darboux.
Resztę załatwia własność Darboux.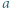 jest cyfrą setek,
jest cyfrą setek, 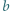 - cyfrą dziesiątek, a
- cyfrą dziesiątek, a  - cyfrą jedności, jest pierwsza. Dowieść, że
- cyfrą jedności, jest pierwsza. Dowieść, że 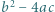 nie jest kwadratem liczby naturalnej.
nie jest kwadratem liczby naturalnej.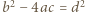 dla pewnej liczby naturalnej
dla pewnej liczby naturalnej 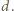 Niech
Niech 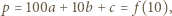 gdzie
gdzie 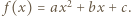 Korzystając z postaci iloczynowej, otrzymamy po przekształceniach
Korzystając z postaci iloczynowej, otrzymamy po przekształceniach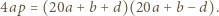
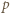 jest pierwsza, więc dzieli co najmniej jedną z liczb:
jest pierwsza, więc dzieli co najmniej jedną z liczb: 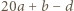 lub
lub 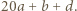 Tu mamy sprzeczność, bo są to liczby dodatnie mniejsze od
Tu mamy sprzeczność, bo są to liczby dodatnie mniejsze od 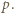
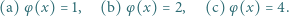
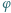 oznacza funkcję Eulera.
oznacza funkcję Eulera.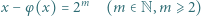
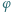 oznacza funkcję Eulera.
oznacza funkcję Eulera.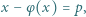
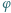 jest funkcją Eulera, a
jest funkcją Eulera, a 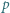 jest daną liczbą pierwszą. Wykazać, że równanie (*):
jest daną liczbą pierwszą. Wykazać, że równanie (*):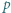 ).
).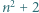 oraz
oraz 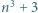 dla pewnej liczby naturalnej
dla pewnej liczby naturalnej 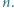
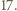
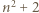 oraz
oraz 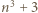 dzieli również liczbę
dzieli również liczbę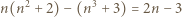
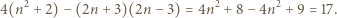
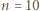 mamy
mamy 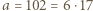 oraz
oraz 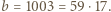
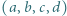 o tej własności, że każdy z iloczynów
o tej własności, że każdy z iloczynów 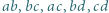 jest o 1 większy od kwadratu pewnej liczby naturalnej.
jest o 1 większy od kwadratu pewnej liczby naturalnej.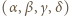 jest dowolną czwórką kolejnych liczb naturalnych nieparzystych, wówczas czwórka
jest dowolną czwórką kolejnych liczb naturalnych nieparzystych, wówczas czwórka 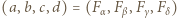 jest dobra; jak zwykle,
jest dobra; jak zwykle, 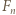 oznacza
oznacza  -tą liczbę Fibonacciego (
-tą liczbę Fibonacciego ( 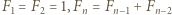 dla
dla 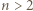 ).
).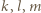 do pełnego bloku siedmiu kolejnych liczb naturalnych
do pełnego bloku siedmiu kolejnych liczb naturalnych 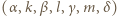 i korzystamy ze znanych tożsamości
i korzystamy ze znanych tożsamości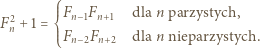
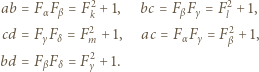
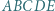 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 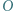 ; przy tym
; przy tym 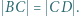 Przekątne
Przekątne 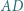 i
i 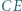 są prostopadłe, zaś przekątne
są prostopadłe, zaś przekątne 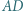 i
i 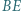 przecinają się w takim punkcie
przecinają się w takim punkcie 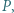 że
że 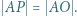 Wykazać, że trójkąt
Wykazać, że trójkąt 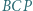 jest równoboczny.
jest równoboczny.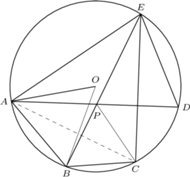
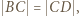 punkt
punkt 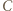 jest środkiem łuku
jest środkiem łuku 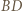 ; zatem prosta
; zatem prosta 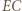 jest dwusieczną kąta wpisanego
jest dwusieczną kąta wpisanego 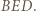 Przy tym jest prostopadła do prostej
Przy tym jest prostopadła do prostej 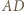 ; jest więc symetralną odcinka
; jest więc symetralną odcinka 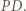 Stąd wynika, że
Stąd wynika, że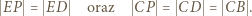
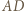 i
i 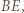 przecinające się w punkcie
przecinające się w punkcie 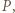 wyznaczają trójkąty podobne:
wyznaczają trójkąty podobne: 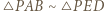 ; a ponieważ
; a ponieważ 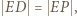 zatem
zatem 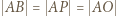 (ostatnia równość jest dana w założeniach). To pokazuje, że trójkąt
(ostatnia równość jest dana w założeniach). To pokazuje, że trójkąt 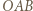 jest równoboczny, wobec czego
jest równoboczny, wobec czego 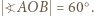 W takim razie
W takim razie 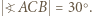
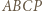 to deltoid
to deltoid 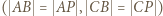 ; stąd
; stąd 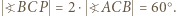 Wobec wcześniejszego spostrzeżenia, że
Wobec wcześniejszego spostrzeżenia, że 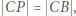 dostajemy tezę zadania: trójkąt
dostajemy tezę zadania: trójkąt 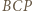 jest równoboczny.
jest równoboczny.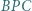 i
i 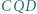 są równoboczne i leżą na zewnątrz równoległoboku
są równoboczne i leżą na zewnątrz równoległoboku 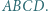 Udowodnić, że trójkąt
Udowodnić, że trójkąt 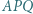 też jest równoboczny.
też jest równoboczny.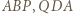 i
i 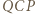 są przystające (bkb).
są przystające (bkb).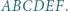 Punkty
Punkty 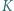 i
i 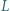 są środkami odcinków odpowiednio
są środkami odcinków odpowiednio 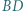 i
i 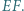 Dowieść, że trójkąt
Dowieść, że trójkąt 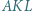 jest równoboczny.
jest równoboczny.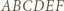 na
na 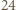 przystające trójkąty równoboczne można zauważyć, że odcinki
przystające trójkąty równoboczne można zauważyć, że odcinki 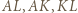 są dłuższymi przekątnymi przystających równoległoboków
są dłuższymi przekątnymi przystających równoległoboków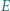 i
i 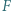 leżą odpowiednio na bokach
leżą odpowiednio na bokach 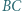 i
i 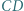 prostokąta
prostokąta 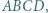 przy czym trójkąt
przy czym trójkąt 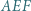 jest równoboczny. Punkt
jest równoboczny. Punkt 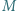 jest środkiem odcinka
jest środkiem odcinka 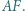 Wykazać, że trójkąt
Wykazać, że trójkąt 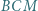 jest równoboczny.
jest równoboczny.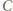 i
i 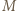 leżą na okręgu o średnicy
leżą na okręgu o średnicy 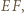 więc
więc 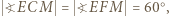 analogicznie
analogicznie 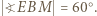
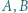 i
i 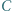 leżą kolejno na prostej
leżą kolejno na prostej 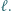 Punkty
Punkty 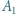 i
i 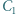 leżą po tej samej stronie prostej
leżą po tej samej stronie prostej 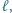 przy czym trójkąty
przy czym trójkąty 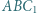 i
i 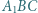 są równoboczne. Punkty
są równoboczne. Punkty 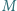 i
i 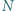 są środkami odcinków odpowiednio
są środkami odcinków odpowiednio 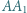 i
i 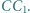 Udowodnić, że trójkąt
Udowodnić, że trójkąt 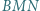 jest równoboczny.
jest równoboczny.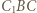 wokół punktu
wokół punktu 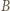 o
o 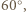 otrzymamy trójkąt
otrzymamy trójkąt 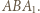 Obrazem punktu
Obrazem punktu 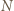 w tym obrocie jest punkt
w tym obrocie jest punkt 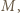 więc
więc 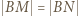 i
i 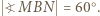
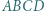 i punkt
i punkt 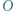 wewnątrz niego, przy czym zachodzą równości:
wewnątrz niego, przy czym zachodzą równości: 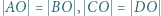 i
i 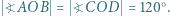 Dowieść, że środki odcinków
Dowieść, że środki odcinków 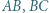 i
i 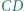 są wierzchołkami trójkąta równobocznego.
są wierzchołkami trójkąta równobocznego.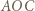 o
o 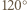 wokół punktu
wokół punktu 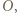 otrzymamy trójkąt
otrzymamy trójkąt 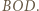 Zatem te trójkąty są przystające oraz proste
Zatem te trójkąty są przystające oraz proste 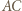 i
i 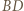 przecinają się pod kątem
przecinają się pod kątem 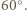
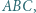 na zewnątrz niego, zbudowano trójkąty równoboczne
na zewnątrz niego, zbudowano trójkąty równoboczne 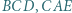 i
i 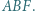 Środkami tych trójkątów są odpowiednio punkty
Środkami tych trójkątów są odpowiednio punkty 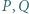 i
i 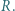 Dowieść, że trójkąt
Dowieść, że trójkąt 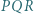 jest równoboczny (twierdzenie Napoleona).
jest równoboczny (twierdzenie Napoleona).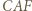 jest podobny do trójkąta
jest podobny do trójkąta 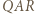 w skali
w skali 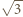 (bkb), analogicznie trójkąt
(bkb), analogicznie trójkąt 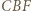 do
do 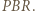 Stąd
Stąd 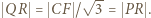 Tą samą metodą dowodzimy, że
Tą samą metodą dowodzimy, że 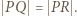
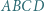 o podstawach
o podstawach 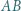 i
i 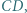 w którym
w którym 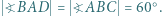 Na boku
Na boku 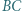 tego trapezu leży taki punkt
tego trapezu leży taki punkt 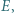 że
że 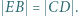 Wykazać, że
Wykazać, że 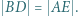
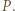 Wówczas trójkąty
Wówczas trójkąty 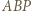 i
i 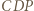 są równoboczne, dalej dowodzimy, że trójkąty
są równoboczne, dalej dowodzimy, że trójkąty 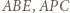 i
i 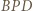 są przystające (bkb).
są przystające (bkb).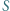 leży wewnątrz sześciokąta foremnego
leży wewnątrz sześciokąta foremnego 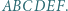 Udowodnić, że suma pól trójkątów
Udowodnić, że suma pól trójkątów 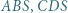 i
i 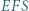 jest równa sumie pól trójkątów
jest równa sumie pól trójkątów 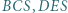 i
i 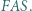
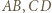 i
i 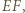 otrzymując trójkąt równoboczny. Suma pól trójkątów
otrzymując trójkąt równoboczny. Suma pól trójkątów 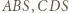 i
i 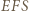 stanowi
stanowi 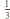 pola tego trójkąta.
pola tego trójkąta.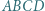 mamy
mamy 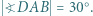 Wykazać, że
Wykazać, że 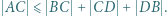
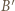 będzie punktem symetrycznym do
będzie punktem symetrycznym do 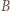 względem prostej
względem prostej 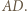 Wówczas trójkąt
Wówczas trójkąt 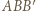 jest równoboczny oraz
jest równoboczny oraz