Zadania z matematyki - IV 2020»Zadanie 1635
o zadaniu...
- Zadanie pochodzi z artykułu Zadania z matematyki - IV 2020
- Publikacja w Delcie: kwiecień 2020
- Publikacja elektroniczna: 31 sierpnia 2020
Prostokąt nazwiemy parzystym, jeśli każdy z jego wymiarów jest parzystą liczbą całkowitą. Kwadrat 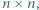 gdzie
gdzie 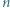 jest liczbą nieparzystą, podzielono na części, z których każda jest parzystym prostokątem lub kwadratem
jest liczbą nieparzystą, podzielono na części, z których każda jest parzystym prostokątem lub kwadratem  Znaleźć najmniejszą możliwą liczbę kwadratów
Znaleźć najmniejszą możliwą liczbę kwadratów  uzyskanych w takim podziale.
uzyskanych w takim podziale.
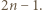
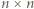 na
na 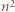 kwadratów jednostkowych, zwanych dalej polami, i wyróżnijmy pola znajdujące się na przecięciach wierszy i kolumn o parzystych numerach. Takich pól jest
kwadratów jednostkowych, zwanych dalej polami, i wyróżnijmy pola znajdujące się na przecięciach wierszy i kolumn o parzystych numerach. Takich pól jest 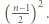
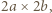 a więc o polu
a więc o polu 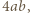 zawiera dokładnie
zawiera dokładnie 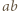 wyróżnionych pól. Wobec tego łączne pole części podziału będących parzystymi prostokątami jest równe co najwyżej
wyróżnionych pól. Wobec tego łączne pole części podziału będących parzystymi prostokątami jest równe co najwyżej 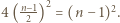 Łączne pole kwadratów jednostkowych jest zatem równe co najmniej
Łączne pole kwadratów jednostkowych jest zatem równe co najmniej 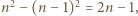 skąd wniosek, że jest co najmniej tyle takich kwadratów.
skąd wniosek, że jest co najmniej tyle takich kwadratów.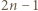 kwadratów jednostkowych, jest możliwy - wystarczy wyciąć kwadrat o boku
kwadratów jednostkowych, jest możliwy - wystarczy wyciąć kwadrat o boku  a pozostałą część podzielić na kwadraty jednostkowe.
a pozostałą część podzielić na kwadraty jednostkowe.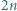 -kąta foremnego oznaczono przez
-kąta foremnego oznaczono przez 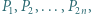 niekoniecznie w tej kolejności. Udowodnić, że łamana zamknięta
niekoniecznie w tej kolejności. Udowodnić, że łamana zamknięta 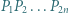 zawiera parę odcinków równoległych.
zawiera parę odcinków równoległych.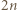 oraz oznaczmy przez
oraz oznaczmy przez 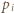 resztę przyporządkowaną wierzchołkowi
resztę przyporządkowaną wierzchołkowi 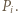
 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 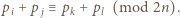 Przypuśćmy nie wprost, że liczby
Przypuśćmy nie wprost, że liczby 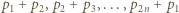 dają parami różne reszty przy dzieleniu przez
dają parami różne reszty przy dzieleniu przez 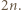 Wówczas ich suma daje resztę
Wówczas ich suma daje resztę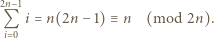
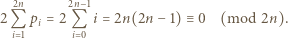
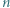 przekątnych
przekątnych 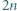 -kąta foremnego przecina się w jednym punkcie, który nie jest wierzchołkiem tego wielokąta. Wykazać, że jest jego środkiem.
-kąta foremnego przecina się w jednym punkcie, który nie jest wierzchołkiem tego wielokąta. Wykazać, że jest jego środkiem.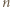 przekątnych. Ponieważ pozostałych
przekątnych. Ponieważ pozostałych 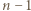 przekątnych ją przecina, więc po obu stronach rozważanej przekątnej znajduje się po
przekątnych ją przecina, więc po obu stronach rozważanej przekątnej znajduje się po 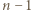 wierzchołków wielokąta. Stąd wniosek, że ta przekątna łączy przeciwległe wierzchołki
wierzchołków wielokąta. Stąd wniosek, że ta przekątna łączy przeciwległe wierzchołki 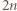 -kąta foremnego, więc przechodzi przez jego środek.
-kąta foremnego, więc przechodzi przez jego środek.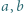 określamy funkcję
określamy funkcję 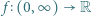 wzorem
wzorem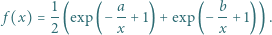
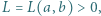 dla której
dla której 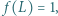 i że
i że 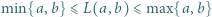 ; zatem liczba
; zatem liczba 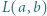 może być uważana za pewną średnią liczb
może być uważana za pewną średnią liczb 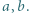
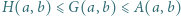 między średnimi: harmoniczną, geometryczną i arytmetyczną liczb
między średnimi: harmoniczną, geometryczną i arytmetyczną liczb 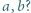
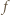 jest ciągła i rosnąca, a jej granice przy końcach dziedziny
jest ciągła i rosnąca, a jej granice przy końcach dziedziny 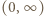 wynoszą 0 oraz
wynoszą 0 oraz 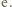 Zatem liczba
Zatem liczba 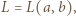 dla której
dla której 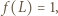 jest jednoznacznie określona. Wykażemy, że
jest jednoznacznie określona. Wykażemy, że 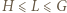 (gdzie
(gdzie  ); stąd też wyniknie, że
); stąd też wyniknie, że 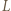 leży pomiędzy
leży pomiędzy 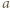 i
i  Wobec ścisłej monotoniczności funkcji
Wobec ścisłej monotoniczności funkcji 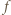 wystarczy dowieść, że
wystarczy dowieść, że 
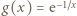 dla
dla 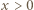 ; jest to funkcja rosnąca. Skoro
; jest to funkcja rosnąca. Skoro 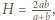 zatem
zatem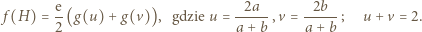
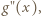 stwierdzamy, że funkcja
stwierdzamy, że funkcja 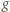 jest wklęsła w przedziale
jest wklęsła w przedziale 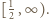 Jeżeli więc liczby
Jeżeli więc liczby 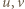 leżą w tym przedziale, to
leżą w tym przedziale, to 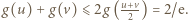 Jeśli zaś np.
Jeśli zaś np. 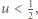 rozważamy dwa podprzypadki (pamiętając, że
rozważamy dwa podprzypadki (pamiętając, że 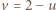 ):
):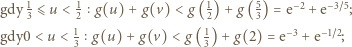
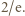 Otrzymane oszacowanie
Otrzymane oszacowanie 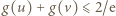 pokazuje (zgodnie ze wzorem (1)), że
pokazuje (zgodnie ze wzorem (1)), że 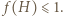
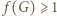 ; do tego użyjemy funkcji
; do tego użyjemy funkcji 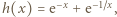 bowiem
bowiem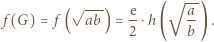
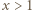 zachodzi nierówność
zachodzi nierówność 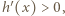 czyli
czyli 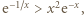 równoważna (przez logarytmowanie) nierówności
równoważna (przez logarytmowanie) nierówności 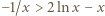 ; tę ostatnią nierówność sprawdzamy bez trudu, przenosząc wszystko na jedną stronę i ponownie różniczkując. Zatem istotnie
; tę ostatnią nierówność sprawdzamy bez trudu, przenosząc wszystko na jedną stronę i ponownie różniczkując. Zatem istotnie 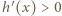 dla
dla 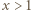 ; stąd
; stąd 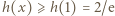 dla
dla 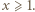 Ponieważ bez straty ogólności można przyjąć, że
Ponieważ bez straty ogólności można przyjąć, że 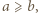 ze wzoru (2) wnosimy, że
ze wzoru (2) wnosimy, że 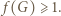 To kończy rozwiązanie.
To kończy rozwiązanie. będzie dowolną dodatnią liczbą nieparzystą. Spójrzmy na ciąg
będzie dowolną dodatnią liczbą nieparzystą. Spójrzmy na ciąg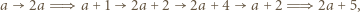
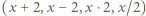 , zaś podwójna strzałka
, zaś podwójna strzałka 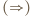 oznacza wielokrotne dodanie lub odjęcie dwójki, przebiegające monotonicznie przez wszystkie liczby tej samej parzystości, co liczby połączone tą podwójną strzałką. Na przykład dla
oznacza wielokrotne dodanie lub odjęcie dwójki, przebiegające monotonicznie przez wszystkie liczby tej samej parzystości, co liczby połączone tą podwójną strzałką. Na przykład dla 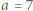 mamy ciąg
mamy ciąg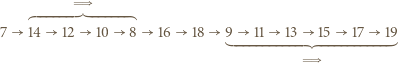
 strzałka
strzałka 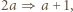 czyli
czyli 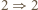 jest "pusta"). W tak określonym ciągu występują wszystkie liczby naturalne z przedziału
jest "pusta"). W tak określonym ciągu występują wszystkie liczby naturalne z przedziału ![|[a, 2a+ 5],](/math/temat/matematyka/teoria_liczb/zadania/2020/03/31/zm-k44-799/10x-22476a16ba6045895876a3c4680af4bf9c980bb5-im-66,57,43-FF,FF,FF.gif) każda jednorazowo.
każda jednorazowo. wzorem rekurencyjnym
wzorem rekurencyjnym 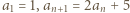 i zastosować podaną konstrukcję w każdym z przedziałów
i zastosować podaną konstrukcję w każdym z przedziałów ![[an,an+1].](/math/temat/matematyka/teoria_liczb/zadania/2020/03/31/zm-k44-799/3x-e1232ec1a01b8b6c5574063abc2b7eaab9e77fab-im-66,57,43-FF,FF,FF.gif)
 występuje dokładnie raz. Udowodnić, że żadna z tych liczb nie jest dzielnikiem innej.
występuje dokładnie raz. Udowodnić, że żadna z tych liczb nie jest dzielnikiem innej. i
i 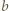 spośród danych w zadaniu. Mamy
spośród danych w zadaniu. Mamy 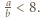 Jeśli
Jeśli  to niech
to niech 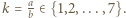 Wówczas
Wówczas 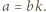 Teraz trzeba zauważyć, że liczby
Teraz trzeba zauważyć, że liczby 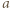 i
i  dają resztę 1 z dzielenia przez 9, co wymusza
dają resztę 1 z dzielenia przez 9, co wymusza 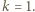
 nie występuje żadna z cyfr 1, 2, 9. Udowodnić, że w zapisie dziesiętnym liczby
nie występuje żadna z cyfr 1, 2, 9. Udowodnić, że w zapisie dziesiętnym liczby 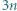 występuje co najmniej jedna z tych cyfr.
występuje co najmniej jedna z tych cyfr.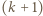 -cyfrowa. Możemy zapisać
-cyfrowa. Możemy zapisać 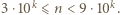 Wystarczy teraz wykazać, że jeśli liczba
Wystarczy teraz wykazać, że jeśli liczba  ma tyle samo cyfr co
ma tyle samo cyfr co 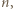 to jej pierwszą cyfrą jest 9, a jeśli ma o jedną cyfrę więcej, to jej pierwszą cyfrą jest 1 lub 2.
to jej pierwszą cyfrą jest 9, a jeśli ma o jedną cyfrę więcej, to jej pierwszą cyfrą jest 1 lub 2. jest dziewięć cyfr, każda inna. Wiedząc to, bez obliczania
jest dziewięć cyfr, każda inna. Wiedząc to, bez obliczania 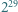 wyznaczyć cyfrę, która w tej liczbie nie występuje.
wyznaczyć cyfrę, która w tej liczbie nie występuje.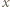 jest brakującą cyfrą, to suma cyfr liczby
jest brakującą cyfrą, to suma cyfr liczby  wynosi
wynosi  Zauważmy, że liczba
Zauważmy, że liczba  daje resztę 1 z dzielenia przez 9, więc liczba
daje resztę 1 z dzielenia przez 9, więc liczba 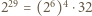 daje resztę 5 z dzielenia przez 9. Wystarczy porównać obie reszty.
daje resztę 5 z dzielenia przez 9. Wystarczy porównać obie reszty.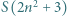 nie jest kwadratem liczby całkowitej dla żadnego naturalnego
nie jest kwadratem liczby całkowitej dla żadnego naturalnego 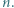
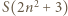 daje taką samą resztę z dzielenia przez 9, co
daje taką samą resztę z dzielenia przez 9, co 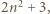 czyli 2, 3, 5 lub 8.
czyli 2, 3, 5 lub 8.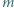 i
i 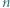 zachodzi nierówność
zachodzi nierówność 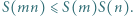
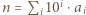 i
i 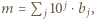 otrzymamy
otrzymamy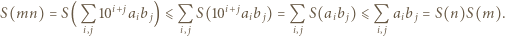
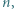 które spełniają równość
które spełniają równość 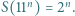
 Wobec tego dla
Wobec tego dla 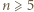 zachodzą nierówności
zachodzą nierówności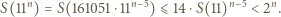
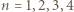 mamy
mamy 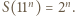
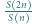 dla całkowitych dodatnich
dla całkowitych dodatnich 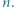

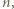 dla których osiągane są skrajne wartości.
dla których osiągane są skrajne wartości.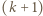 -cyfrową
-cyfrową 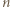 o pierwszej cyfrze
o pierwszej cyfrze 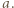 Iloczyn cyfr liczby
Iloczyn cyfr liczby 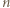 nie przekracza
nie przekracza 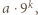 natomiast
natomiast  Taka liczba nie istnieje.
Taka liczba nie istnieje. liczby
liczby 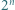 i
i 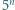 mają taką samą pierwszą cyfrę. Wykazać, że tą cyfrą jest 3.
mają taką samą pierwszą cyfrę. Wykazać, że tą cyfrą jest 3. będzie pierwszą cyfrą
będzie pierwszą cyfrą 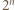 i
i 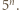 Zapiszmy
Zapiszmy 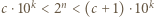 oraz
oraz 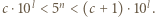 Mnożąc te dwie nierówności, otrzymamy
Mnożąc te dwie nierówności, otrzymamy 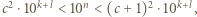 z czego wnioskujemy, że
z czego wnioskujemy, że  i w konsekwencji
i w konsekwencji 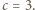
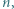 dla których
dla których 
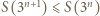 zachodzi tylko dla skończenie wielu
zachodzi tylko dla skończenie wielu 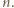 Wtedy istnieje takie
Wtedy istnieje takie  że dla wszystkich
że dla wszystkich 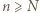 mamy
mamy 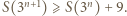 Stąd dla wszystkich
Stąd dla wszystkich 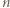 zachodzi nierówność
zachodzi nierówność 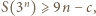 gdzie
gdzie  jest pewną stałą. Z drugiej strony,
jest pewną stałą. Z drugiej strony, 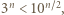 więc liczba
więc liczba  ma co najwyżej
ma co najwyżej 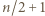 cyfr.
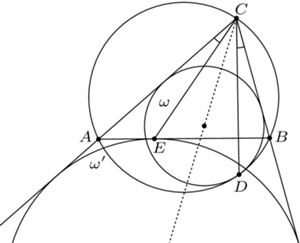
cyfr.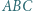 wpisany w okrąg
wpisany w okrąg  Okrąg
Okrąg 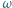 jest styczny do odcinków
jest styczny do odcinków  i
i 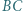 oraz do okręgu
oraz do okręgu  w punkcie
w punkcie 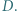 Okrąg
Okrąg 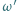 zaś jest dopisany do trójkąta
zaś jest dopisany do trójkąta 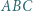 i styczny do boku
i styczny do boku  w punkcie
w punkcie 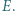 Wykazać, że
Wykazać, że 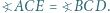
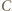 i promieniu
i promieniu 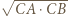 z symetrią względem dwusiecznej kąta
z symetrią względem dwusiecznej kąta 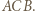 Przekształcenie to zamienia półproste
Przekształcenie to zamienia półproste 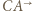 i
i 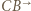 oraz prostą
oraz prostą  z okręgiem
z okręgiem 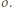 W takim razie okrąg
W takim razie okrąg  przejdzie na okrąg styczny do prostej
przejdzie na okrąg styczny do prostej 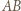 i półprostych
i półprostych 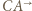 i
i  czyli na okrąg
czyli na okrąg 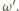 Stąd wniosek, że obrazem punktu
Stąd wniosek, że obrazem punktu 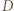 jest punkt
jest punkt 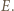 Półprosta
Półprosta 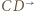 przejdzie więc na półprostą
przejdzie więc na półprostą 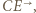 a skoro inwersja zachowuje kąty, to
a skoro inwersja zachowuje kąty, to 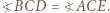
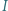 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 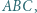 zaś
zaś  jest okręgiem opisanym na tym trójkącie. Okrąg
jest okręgiem opisanym na tym trójkącie. Okrąg 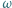 styczny do odcinków
styczny do odcinków 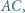
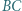 jest styczny do okręgu
jest styczny do okręgu  w punkcie
w punkcie 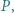 a
a  jest środkiem tego łuku
jest środkiem tego łuku 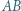 okręgu
okręgu 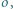 na którym leży punkt
na którym leży punkt 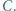 Wykazać, że punkty
Wykazać, że punkty 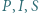 są współliniowe.
są współliniowe.
 to punkty
to punkty 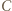 i
i 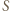 pokrywają się i punkty
pokrywają się i punkty 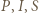 leżą na dwusiecznej
leżą na dwusiecznej 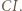 Dalej zakładamy, że
Dalej zakładamy, że 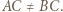 Wówczas punkty
Wówczas punkty 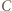 i
i 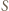 są różne, zaś proste
są różne, zaś proste 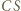 i
i 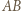 nie są równoległe. Rozważmy złożenie inwersji o środku
nie są równoległe. Rozważmy złożenie inwersji o środku 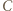 i promieniu
i promieniu 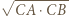 z symetrią względem dwusiecznej kąta
z symetrią względem dwusiecznej kąta 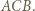 Przekształcenie to zamienia półproste
Przekształcenie to zamienia półproste 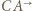 i
i 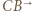 oraz prostą
oraz prostą  z okręgiem
z okręgiem 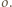 Tak jak w poprzednim zadaniu uzasadniamy, że obrazem okręgu
Tak jak w poprzednim zadaniu uzasadniamy, że obrazem okręgu 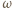 jest okrąg dopisany do trójkąta
jest okrąg dopisany do trójkąta 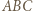 styczny do boku
styczny do boku 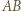 w punkcie
w punkcie  który jest obrazem punktu
który jest obrazem punktu 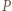 w tym przekształceniu. Ponieważ
w tym przekształceniu. Ponieważ 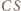 jest dwusieczną kąta zewnętrznego przy wierzchołku
jest dwusieczną kąta zewnętrznego przy wierzchołku 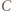 trójkąta
trójkąta 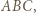 to proste
to proste  i
i 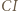 są prostopadłe. W takim razie obrazem punktu
są prostopadłe. W takim razie obrazem punktu 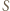 jest punkt
jest punkt  przecięcia prostej
przecięcia prostej 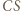 (która jest swoim własnym obrazem) z prostą
(która jest swoim własnym obrazem) z prostą  (która jest obrazem okręgu
(która jest obrazem okręgu  ). Niech
). Niech  będzie obrazem punktu
będzie obrazem punktu 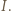 Wtedy z definicji inwersji mamy
Wtedy z definicji inwersji mamy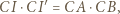

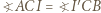 (bo inwersja zachowuje kąty) otrzymujemy, że trójkąty
(bo inwersja zachowuje kąty) otrzymujemy, że trójkąty 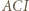 i
i  są podobne. W takim razie
są podobne. W takim razie 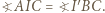 Ponieważ
Ponieważ 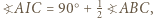 to mamy
to mamy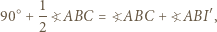
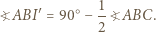
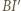 jest dwusieczną kąta zewnętrznego przy wierzchołku
jest dwusieczną kąta zewnętrznego przy wierzchołku 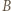 trójkąta
trójkąta 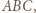 więc
więc 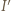 jest środkiem okręgu dopisanego do trójkąta
jest środkiem okręgu dopisanego do trójkąta 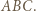 W takim razie
W takim razie  co wraz z równością
co wraz z równością 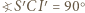 (bo
(bo 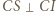 ) oznacza, że punkty
) oznacza, że punkty 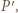
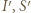 i
i 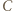 leżą na jednym okręgu. To zaś jest równoważne z tym, że punkty
leżą na jednym okręgu. To zaś jest równoważne z tym, że punkty  są współliniowe.
są współliniowe.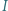 jest wpisany w trójkąt
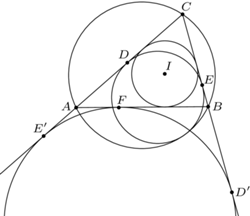
jest wpisany w trójkąt 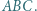 Okrąg
Okrąg 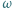 styczny do okręgu opisanego na trójkącie
styczny do okręgu opisanego na trójkącie 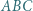 jest styczny do odcinków
jest styczny do odcinków 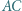 i
i 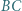 odpowiednio w punktach
odpowiednio w punktach 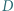 i
i 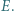 Wykazać, że punkt
Wykazać, że punkt  leży na odcinku
leży na odcinku 
 to połowa obwodu trójkąta
to połowa obwodu trójkąta  to miara kąta
to miara kąta 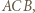 zaś
zaś  to promień okręgu wpisanego w trójkąt
to promień okręgu wpisanego w trójkąt 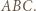 Inwersja o środku
Inwersja o środku 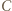 i promieniu
i promieniu 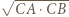 złożona z symetrią względem dwusiecznej kąta
złożona z symetrią względem dwusiecznej kąta 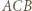 przeprowadza okrąg
przeprowadza okrąg 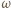 na okrąg dopisany do trójkąta
na okrąg dopisany do trójkąta 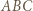 styczny do boku
styczny do boku 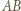 w punkcie
w punkcie 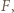 a punkty
a punkty 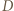 i
i 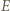 odpowiednio na punkty
odpowiednio na punkty 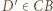 i
i  Ponieważ
Ponieważ  i
i 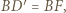 to
to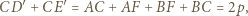
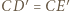 prowadzi do wniosku, że
prowadzi do wniosku, że 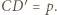 Z drugiej strony z definicji inwersji mamy
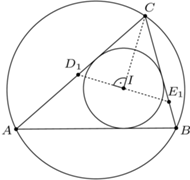
Z drugiej strony z definicji inwersji mamy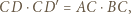
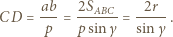
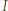 i prostopadła do prostej
i prostopadła do prostej 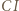 przecina boki
przecina boki 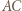 i
i 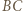 odpowiednio w punktach
odpowiednio w punktach 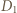 i
i 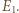 Skoro
Skoro  to odległość punktu
to odległość punktu  od prostej
od prostej 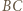 jest równa
jest równa 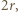 skąd wniosek, że
skąd wniosek, że 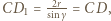 czyli
czyli  Analogicznie uzasadnimy, że
Analogicznie uzasadnimy, że  więc punkt
więc punkt 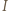 leży na odcinku
leży na odcinku 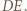
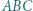 jest wpisany w okrąg
jest wpisany w okrąg 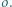 Punkty
Punkty 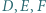 są środkami łuków
są środkami łuków 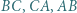 niezawierających pozostałych wierzchołków trójkąta. Punkty
niezawierających pozostałych wierzchołków trójkąta. Punkty 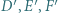 są symetryczne do punktów
są symetryczne do punktów 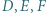 odpowiednio względem boków
odpowiednio względem boków 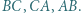 Wykazać, że punkty
Wykazać, że punkty  oraz ortocentrum trójkąta
oraz ortocentrum trójkąta 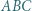 leżą na jednym okręgu.
leżą na jednym okręgu. i
i  będą spodkami wysokości trójkąta
będą spodkami wysokości trójkąta 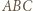 poprowadzonymi odpowiednio z wierzchołków
poprowadzonymi odpowiednio z wierzchołków  Ponieważ na czworokątach
Ponieważ na czworokątach 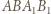 i
i 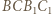 można opisać okręgi, to
można opisać okręgi, to
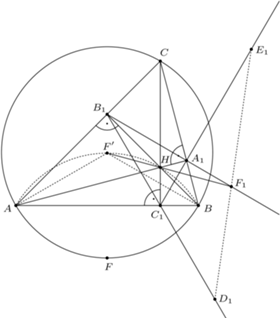
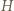 i promieniu
i promieniu  złożoną z symetrią środkową względem punktu
złożoną z symetrią środkową względem punktu 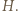 Obrazami punktów
Obrazami punktów 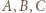 są zatem punkty
są zatem punkty 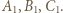 Ponieważ
Ponieważ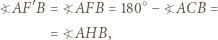
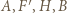 leżą na jednym okręgu, który w rozważanym przekształceniu przechodzi na prostą
leżą na jednym okręgu, który w rozważanym przekształceniu przechodzi na prostą  Obrazem punktu
Obrazem punktu  jest punkt
jest punkt 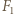 przecięcia prostych
przecięcia prostych  i
i 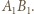 Analogicznie stwierdzamy, że w tym przekształceniu punkt
Analogicznie stwierdzamy, że w tym przekształceniu punkt 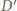 przechodzi na punkt
przechodzi na punkt 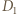 przecięcia prostych
przecięcia prostych 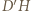 i
i 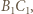 a punkt
a punkt 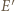 przechodzi na punkt
przechodzi na punkt 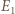 przecięcia prostych
przecięcia prostych 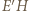 i
i 
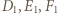 leżą na jednej prostej. Stosując twierdzenie Menelausa dla trójkąta
leżą na jednej prostej. Stosując twierdzenie Menelausa dla trójkąta 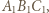 widzimy, że wystarczy wykazać, że
widzimy, że wystarczy wykazać, że
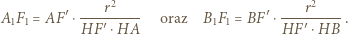
 widzimy, że
widzimy, że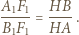

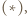 co kończy rozwiązanie.
co kończy rozwiązanie.