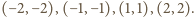Klub 44M - zadania II 2013»Zadanie 655
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania II 2013
- Publikacja w Delcie: luty 2013
- Publikacja elektroniczna: 31 stycznia 2013
- Artykuł źródłowy w wersji do druku [application/pdf]: (192 KB)
Punkt
 leży na boku
leży na boku
 trójkąta
trójkąta
 Punkt
Punkt
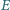 jest środkiem okręgu dopisanego, stycznego do boku
jest środkiem okręgu dopisanego, stycznego do boku
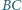 oraz
przedłużeń boków
oraz
przedłużeń boków
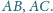 Punkt
Punkt
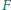 jest środkiem
okręgu wpisanego w trójkąt
jest środkiem
okręgu wpisanego w trójkąt
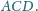 Dowieść, że jeżeli trójkąt
Dowieść, że jeżeli trójkąt
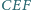 jest równoramienny, to także trójkąt
jest równoramienny, to także trójkąt
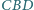 jest
równoramienny.
jest
równoramienny.
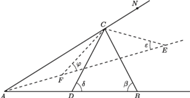
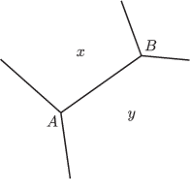
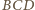 przy wierzchołkach
przy wierzchołkach
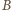 i
i
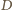 przez
przez
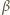 i
i
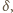 a miary kątów trójkąta
a miary kątów trójkąta
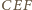 przy
wierzchołkach
przy
wierzchołkach
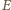 i
i
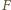 przez
przez
 i
i
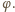
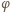 i
i
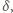 jako kąty zewnętrzne trójkątów
jako kąty zewnętrzne trójkątów
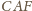 i
i
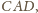 są związane zależnością
są związane zależnością
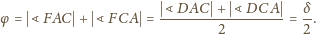
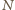 będzie dowolnym punktem na przedłużeniu boku
będzie dowolnym punktem na przedłużeniu boku
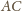 poza wierzchołek
poza wierzchołek
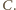 Kąty
Kąty
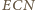 i
i
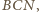 jako
kąty zewnętrzne trójkątów
jako
kąty zewnętrzne trójkątów
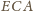 i
i
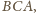 wyrażają się
jako sumy:
wyrażają się
jako sumy:
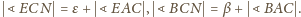 Tak
więc
Tak
więc
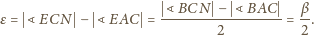
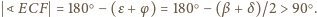 Zatem jeśli
trójkąt
Zatem jeśli
trójkąt
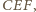 z kątem rozwartym przy wierzchołku
z kątem rozwartym przy wierzchołku
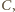 jest
równoramienny, to
jest
równoramienny, to
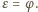 Z uzyskanych wcześniej równości
dostajemy wówczas
Z uzyskanych wcześniej równości
dostajemy wówczas
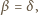 czyli równoramienność trójkąta
czyli równoramienność trójkąta
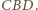
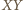 nazywamy płaszczyznę do niego
prostopadłą, przechodzącą przez jego środek.
nazywamy płaszczyznę do niego
prostopadłą, przechodzącą przez jego środek.
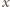 naszego wielościanu. Płaszczyzny
symetralne krawędzi tej ściany przecinają się wszystkie wzdłuż prostej
naszego wielościanu. Płaszczyzny
symetralne krawędzi tej ściany przecinają się wszystkie wzdłuż prostej
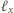 prostopadłej do ściany
prostopadłej do ściany
 i przechodzącej przez środek
okręgu opisanego na tej ścianie. Ta prosta jest zbiorem środków wszystkich
sfer zawierających wszystkie wierzchołki ściany
i przechodzącej przez środek
okręgu opisanego na tej ścianie. Ta prosta jest zbiorem środków wszystkich
sfer zawierających wszystkie wierzchołki ściany
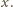
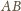 będzie wspólną krawędzią sąsiednich ścian
będzie wspólną krawędzią sąsiednich ścian
 i
i
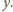 Proste
Proste
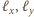 nie są równoległe i obie leżą
w płaszczyźnie symetralnej
nie są równoległe i obie leżą
w płaszczyźnie symetralnej
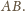 Przecinają się więc w jednym punkcie,
który jest środkiem sfery opisanej na ścianach
Przecinają się więc w jednym punkcie,
który jest środkiem sfery opisanej na ścianach
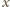 i
i
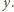
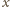 i
i
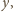 to
jej środek musi leżeć zarówno na prostej
to
jej środek musi leżeć zarówno na prostej
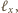 jak i na prostej
jak i na prostej
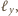 co dowodzi, że ta sfera jest wyznaczona jednoznacznie.
co dowodzi, że ta sfera jest wyznaczona jednoznacznie.

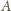 spotykają się trzy krawędzie, to w tym
wierzchołku spotykają się też trzy ściany. Oznaczmy je jak na rysunku.
spotykają się trzy krawędzie, to w tym
wierzchołku spotykają się też trzy ściany. Oznaczmy je jak na rysunku.
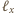 z płaszczyzną symetralną odcinka
z płaszczyzną symetralną odcinka
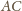 (przyjmujemy definicje i oznaczenia z rozwiązania zadania M
1375). Zauważmy, że należy on też do prostej
(przyjmujemy definicje i oznaczenia z rozwiązania zadania M
1375). Zauważmy, że należy on też do prostej
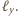 Istotnie,
należy do płaszczyzny symetralnej
Istotnie,
należy do płaszczyzny symetralnej
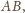 bo prosta
bo prosta
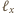 jest
w niej zawarta, i do płaszczyzny symetralnej
jest
w niej zawarta, i do płaszczyzny symetralnej
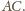 Przecięcie tych
płaszczyzn to właśnie prosta
Przecięcie tych
płaszczyzn to właśnie prosta
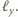 Podobnie, należy on do prostej
Podobnie, należy on do prostej
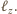 Jest więc równo odległy od wszystkich wierzchołków ścian
Jest więc równo odległy od wszystkich wierzchołków ścian
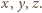
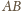 na tej ścieżce, że sfera zawierająca wierzchołki
ścian spotykających się w
na tej ścieżce, że sfera zawierająca wierzchołki
ścian spotykających się w
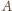 różni się od sfery, w którą są wpisane
ściany spotykające się w
różni się od sfery, w którą są wpisane
ściany spotykające się w
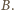 Ale to znaczy, że dla sąsiednich ścian
o wspólnej krawędzi
Ale to znaczy, że dla sąsiednich ścian
o wspólnej krawędzi
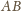 istnieją dwie różne sfery, w które te ściany
są jednocześnie wpisane, co przeczy tezie zadania ZM-1375.
istnieją dwie różne sfery, w które te ściany
są jednocześnie wpisane, co przeczy tezie zadania ZM-1375.
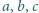 jest nie mniejsza od
jest nie mniejsza od
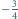 oraz
oraz
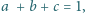 to
to

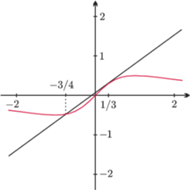
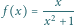
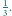
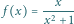
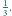
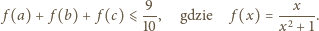
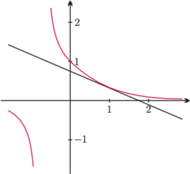
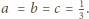 Równanie
stycznej do funkcji
Równanie
stycznej do funkcji
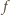 w punkcie
w punkcie
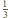 ma postać
ma postać
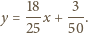
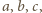 spełniających warunek
spełniających warunek
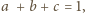 suma wartości wyrażenia
suma wartości wyrażenia
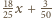 jest równa
jest równa
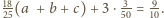
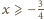 prawdziwa jest
nierówność
prawdziwa jest
nierówność
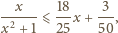
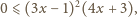
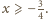
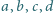 zachodzi
nierówność
zachodzi
nierówność

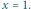
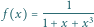
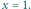
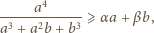
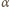 i
i
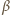 są pewnymi liczbami rzeczywistymi. Dzieląc obie
strony przez
są pewnymi liczbami rzeczywistymi. Dzieląc obie
strony przez
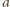 i podstawiając
i podstawiając
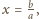 otrzymujemy
otrzymujemy
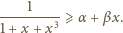
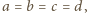 więc musimy tak dobrać współczynniki
więc musimy tak dobrać współczynniki
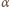 i
i
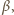 aby równość zachodziła dla
aby równość zachodziła dla
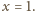 Znajdując
równanie stycznej do wykresu funkcji
Znajdując
równanie stycznej do wykresu funkcji
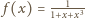 w punkcie
w punkcie
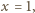 otrzymujemy współczynniki
otrzymujemy współczynniki
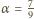 i
i
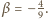
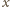 zachodzi
nierówność
zachodzi
nierówność
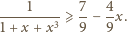
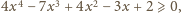 a następnie
doprowadzamy nierówność do postaci
a następnie
doprowadzamy nierówność do postaci
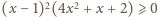 – teraz
widać, że to prawda dla dowolnego
– teraz
widać, że to prawda dla dowolnego
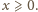
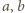 zachodzi nierówność
zachodzi nierówność
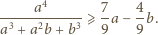
 zachodzi
nierówność
zachodzi
nierówność

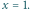
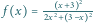
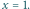
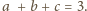 (Jest to bardziej wygodne niż założenie
(Jest to bardziej wygodne niż założenie
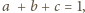 gdyż
równość zachodzi dla
gdyż
równość zachodzi dla
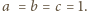 ) Wówczas dana nierówność
przyjmuje postać
) Wówczas dana nierówność
przyjmuje postać
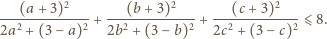
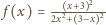 w punkcie
w punkcie
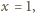 otrzymujemy do udowodnienia nierówność
otrzymujemy do udowodnienia nierówność
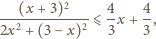
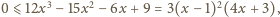 co
jest prawdą dla
co
jest prawdą dla
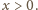
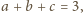 nierówność
zachodzi nie tylko dla liczb dodatnich, ale także dla nie mniejszych niż
nierówność
zachodzi nie tylko dla liczb dodatnich, ale także dla nie mniejszych niż
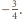
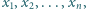 gdzie
gdzie
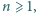 spełniają warunki
spełniają warunki

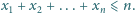
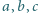 zachodzi
nierówność
zachodzi
nierówność

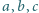 zachodzi
nierówność
zachodzi
nierówność

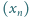 jest określony wzorem rekurencyjnym
jest określony wzorem rekurencyjnym

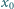 jest dowolną liczbą dodatnią. Obliczyć granicę
jest dowolną liczbą dodatnią. Obliczyć granicę
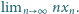
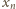 są liczbami dodatnimi. Z nierówności
są liczbami dodatnimi. Z nierówności
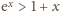 (dla
(dla
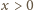 ) wynika, że ciąg
) wynika, że ciąg
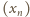 jest malejący –
zatem zbieżny do granicy
jest malejący –
zatem zbieżny do granicy
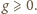 Równanie
Równanie
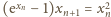 daje
w granicy zależność
daje
w granicy zależność
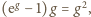 która nie zachodzi dla
żadnej liczby dodatniej
która nie zachodzi dla
żadnej liczby dodatniej
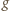 (w myśl tej samej nierówności). Zatem
(w myśl tej samej nierówności). Zatem
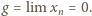
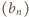 jest ciągiem
rosnącym do nieskończoności, to
jest ciągiem
rosnącym do nieskończoności, to
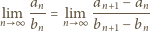
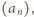 dla którego granica po prawej stronie
istnieje.
dla którego granica po prawej stronie
istnieje.
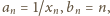 mamy w mianowniku wyrażenia po prawej
stronie jedynkę, a w liczniku:
mamy w mianowniku wyrażenia po prawej
stronie jedynkę, a w liczniku:
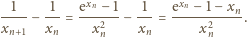
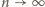 (więc
(więc
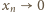 ), ten iloraz dąży do
), ten iloraz dąży do
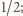 widać
to na przykład z początkowego fragmentu rozwinięcia potęgowego
widać
to na przykład z początkowego fragmentu rozwinięcia potęgowego
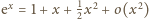 (przy
(przy
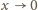 ). Tak więc
). Tak więc
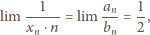
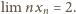
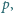 dla której
dla której
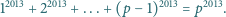
 zachodzi
zachodzi
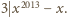 Stąd
Stąd
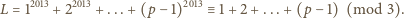
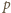 jest postaci
jest postaci
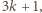 to wówczas
to wówczas
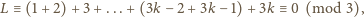
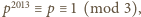 więc równanie nie ma rozwiązania
w tym przypadku. Podobnie stwierdzamy, że dla
więc równanie nie ma rozwiązania
w tym przypadku. Podobnie stwierdzamy, że dla
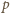 postaci
postaci
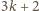 równanie jest sprzeczne. Zatem jedyna możliwość to
równanie jest sprzeczne. Zatem jedyna możliwość to
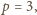 ale łatwo sprawdzić, że wtedy równanie również jest
sprzeczne.
ale łatwo sprawdzić, że wtedy równanie również jest
sprzeczne.
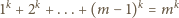
 oraz
oraz
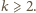 Dziś
wiadomo, że jeśli równanie ma rozwiązanie dla jakiegoś
Dziś
wiadomo, że jeśli równanie ma rozwiązanie dla jakiegoś
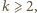 to
to
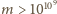 (zgrabny dowód i historia problemu są przedstawione
w artykule: P. Moore, A top hat for Moser’s four mathemagical rabbits, Amer.
Math. Monthly 118 (2011), 364-370).
(zgrabny dowód i historia problemu są przedstawione
w artykule: P. Moore, A top hat for Moser’s four mathemagical rabbits, Amer.
Math. Monthly 118 (2011), 364-370).
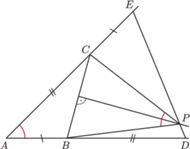
 i takie punkty
i takie punkty
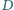 i
i
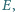 że
że
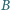 leży na odcinku
leży na odcinku
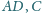 leży na odcinku
leży na odcinku
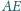 oraz
zachodzą równości
oraz
zachodzą równości
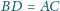 i
i
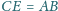 (rysunek). Symetralna
odcinka
(rysunek). Symetralna
odcinka
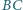 przecina
przecina
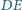 w punkcie
w punkcie
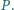 Udowodnić, że
kąty
Udowodnić, że
kąty
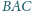 i
i
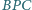 są równe.
są równe.
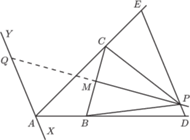
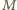 jest środkiem
jest środkiem
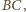 jego odległość od prostej
jego odległość od prostej
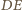 to średnia arytmetyczna odległości punktów
to średnia arytmetyczna odległości punktów
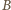 i
i
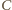 od
od
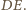 Jest ona równa średniej arytmetycznej odległości tych punktów
od
Jest ona równa średniej arytmetycznej odległości tych punktów
od
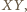 ponieważ
ponieważ
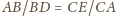 i
i
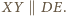 Zatem
Zatem
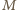 jest równo odległy od
jest równo odległy od
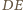 i
i
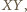 skąd
skąd
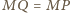 oraz
oraz
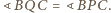
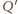 będzie takim punktem na półprostej
będzie takim punktem na półprostej
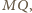 że
że
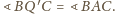 Z podobieństwa trójkątów równoramiennych
Z podobieństwa trójkątów równoramiennych
 i
i
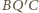 mamy
mamy
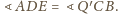 Zatem skoro na
czworokącie
Zatem skoro na
czworokącie
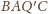 można opisać okrąg, to
można opisać okrąg, to
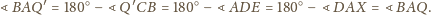
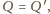 co daje tezę.
co daje tezę.
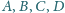 leżą, w tej właśnie kolejności, na prostej
leżą, w tej właśnie kolejności, na prostej
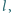 przy
czym
przy
czym
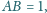
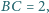
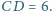 Rozstrzygnij, czy istnieje taki
punkt
Rozstrzygnij, czy istnieje taki
punkt
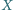 spoza prostej
spoza prostej
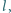 aby
aby
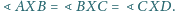

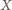 istnieje, to
istnieje, to
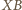 jest dwusieczną kąta
jest dwusieczną kąta
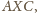 zatem z twierdzenia o dwusiecznej
zatem z twierdzenia o dwusiecznej
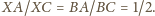 Punkty
Punkty
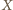 i
i
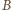 leżą więc na okręgu Apoloniusza dla punktów
leżą więc na okręgu Apoloniusza dla punktów
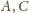 i stałej 1/2. Analogicznie punkty
i stałej 1/2. Analogicznie punkty
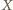 i
i
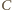 leżą na
okręgu Apoloniusza dla punktów
leżą na
okręgu Apoloniusza dla punktów
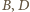 i stałej 1/3.
i stałej 1/3.

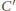 na prostej
na prostej
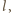 różny od
różny od
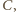 spełnia
warunek
spełnia
warunek
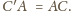 Wtedy
Wtedy
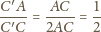
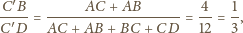
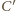 należy do obydwu powyższych okręgów. Średnicą
pierwszego z nich jest więc
należy do obydwu powyższych okręgów. Średnicą
pierwszego z nich jest więc
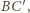 a drugiego –
a drugiego –
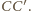 Stąd jedynym
ich wspólnym punktem jest
Stąd jedynym
ich wspólnym punktem jest
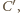 czyli
czyli
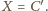 Ale wtedy
Ale wtedy
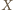 leży na prostej
leży na prostej
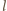 – sprzeczność.
– sprzeczność.
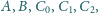 przy czym
przy czym
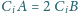 dla
dla
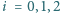 oraz
oraz
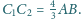 Udowodnij,
że kąt
Udowodnij,
że kąt
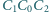 jest prosty i że punkty
jest prosty i że punkty
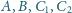 leżą na jednej
płaszczyźnie.
leżą na jednej
płaszczyźnie.

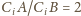 dla
dla
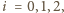 więc wszystkie punkty
więc wszystkie punkty
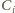 leżą na sferze Apoloniusza dla punktów
leżą na sferze Apoloniusza dla punktów
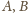 i stałej 2
(zdefiniowanej analogicznie do okręgu). Jej średnicę wyznaczają punkty
i stałej 2
(zdefiniowanej analogicznie do okręgu). Jej średnicę wyznaczają punkty
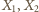 na prostej
na prostej
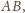 spełniające warunek
spełniające warunek
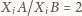 dla
dla
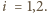 Wówczas
Wówczas
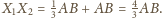
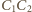 także jest średnicą rozważanej sfery. Stąd
kąt
także jest średnicą rozważanej sfery. Stąd
kąt
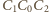 jest prosty, jako wpisany oparty na średnicy. Proste
jest prosty, jako wpisany oparty na średnicy. Proste
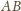 i
i
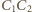 przecinają się (w środku sfery), więc punkty
przecinają się (w środku sfery), więc punkty
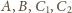 leżą na jednej płaszczyźnie.
leżą na jednej płaszczyźnie.
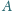 i
i
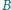 nie należą do płaszczyzny
nie należą do płaszczyzny
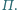 Wyznacz
zbiór wszystkich punktów
Wyznacz
zbiór wszystkich punktów
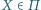 o tej własności, że proste
o tej własności, że proste
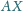 i
i
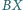 tworzą z płaszczyzną
tworzą z płaszczyzną
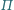 równe kąty.
równe kąty.
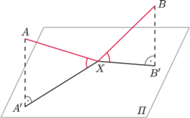
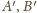 oznaczają odpowiednio rzuty punktów
oznaczają odpowiednio rzuty punktów
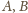 na
płaszczyznę
na
płaszczyznę
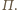 Dla punktu
Dla punktu
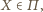 różnego od
różnego od
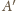 i
i
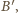 równość
równość
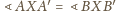 zachodzi wtedy i tylko
wtedy, gdy trójkąty prostokątne
zachodzi wtedy i tylko
wtedy, gdy trójkąty prostokątne
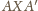 i
i
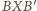 są podobne.
Równoważnie,
są podobne.
Równoważnie,
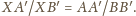 Jeśli
Jeśli
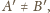 to
punkty
to
punkty
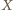 o żądanej własności tworzą okrąg Apoloniusza dla
punktów
o żądanej własności tworzą okrąg Apoloniusza dla
punktów
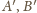 i stałej
i stałej
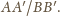 Jakie jest rozwiązanie, gdy
Jakie jest rozwiązanie, gdy
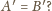 Czy możliwe, by
Czy możliwe, by
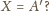
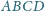 miara kąta wewnętrznego przy wierzchołku
miara kąta wewnętrznego przy wierzchołku
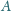 jest większa od
jest większa od
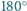 oraz zachodzi równość
oraz zachodzi równość
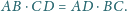 Punkt
Punkt
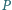 jest symetryczny do punktu
jest symetryczny do punktu
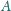 względem prostej
względem prostej
 Udowodnij, że
Udowodnij, że
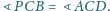
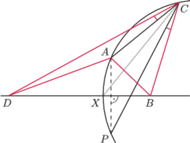
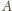 i
i
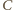 leżą na okręgu Apoloniusza dla punktów
leżą na okręgu Apoloniusza dla punktów
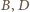 i stałej
i stałej
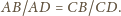 Z symetrii względem prostej
Z symetrii względem prostej
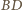 punkt
punkt
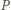 też na nim leży (
też na nim leży (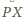 i
i
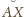 są równe, więc
są równe, więc
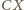 jest dwusieczną kąta
jest dwusieczną kąta
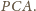 Jednocześnie
Jednocześnie
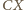 jest też dwusieczną kąta
jest też dwusieczną kąta
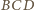 (własność z początku artykułu,
(własność z początku artykułu, 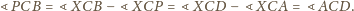
 w którym
w którym
 Na boku
Na boku
 tego prostokąta skonstruuj takie punkty
tego prostokąta skonstruuj takie punkty
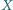 i
i
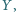 aby
aby
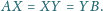
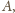 środka boku
środka boku
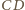 i stałej 2.
i stałej 2.
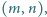 dla których
liczby
dla których
liczby

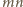 powinien być dzielnikiem liczb
powinien być dzielnikiem liczb
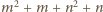 oraz
oraz
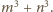 Zatem
Zatem
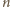 ma być dzielnikiem liczb
ma być dzielnikiem liczb
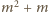 oraz
oraz
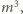 więc także liczby
więc także liczby
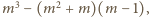 równej
równej
 Przez symetrię, liczba
Przez symetrię, liczba
 ma być dzielnikiem liczby
ma być dzielnikiem liczby
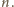 Dostajemy warunek
Dostajemy warunek
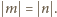
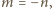 podane w zadaniu sumy wynoszą
podane w zadaniu sumy wynoszą
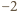 oraz 0
(więc są całkowite). Jeśli zaś
oraz 0
(więc są całkowite). Jeśli zaś
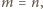 wynoszą one odpowiednio
wynoszą one odpowiednio
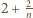 oraz
oraz
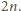 Są one obie całkowite wtedy i tylko wtedy, gdy
Są one obie całkowite wtedy i tylko wtedy, gdy
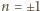 lub
lub
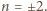
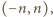 gdzie
gdzie
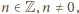 a ponadto cztery pary
a ponadto cztery pary