ZM-11.10-Deltoid-1»Zadanie 1
o zadaniu...
- Zadanie olimpijskie: VI Olimpiada Matematyczna Gimnazjalistów,
- Zadanie pochodzi z artykułu
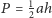
- Publikacja w Delcie: październik 2011
- Publikacja elektroniczna: 02-10-2011
- Artykuł źródłowy w wersji do druku [application/pdf]: (85 KB)
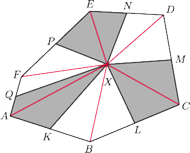
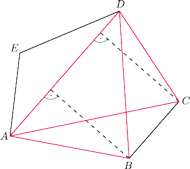
Punkt
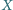 leży wewnątrz sześciokąta wypukłego
leży wewnątrz sześciokąta wypukłego
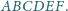 Punkty
Punkty
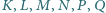 są odpowiednio
środkami boków
są odpowiednio
środkami boków
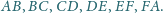 Wykaż, że
Wykaż, że
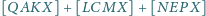 nie zależy od wyboru punktu
nie zależy od wyboru punktu
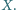
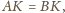 to
to
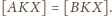 Podobnie
Podobnie
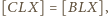
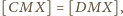
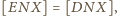
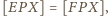
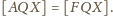 Dodając
stronami, uzyskujemy
Dodając
stronami, uzyskujemy
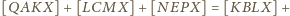
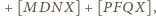 czyli
czyli
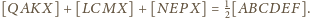
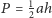
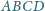 o polu 1. Punkt
o polu 1. Punkt
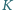 jest
symetryczny do punktu
jest
symetryczny do punktu
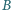 względem punktu
względem punktu
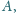 punkt
punkt
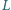 jest
symetryczny do punktu
jest
symetryczny do punktu
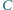 względem punktu
względem punktu
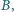 punkt
punkt
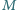 jest symetryczny do punktu
jest symetryczny do punktu
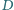 względem punktu
względem punktu
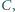 punkt
punkt
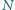 jest symetryczny do punktu
jest symetryczny do punktu
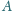 względem
punktu
względem
punktu
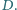 Oblicz
Oblicz
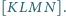
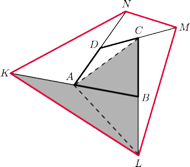
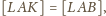 bo trójkąty te mają równe
podstawy
bo trójkąty te mają równe
podstawy
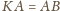 i wspólną wysokość z
i wspólną wysokość z
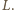 Ponadto
Ponadto
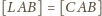 (ponieważ
(ponieważ
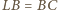 ). Analogicznie
). Analogicznie
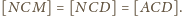 Stąd
Stąd
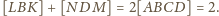 Podobnie
Podobnie
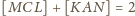 i ostatecznie
i ostatecznie
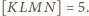
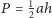
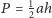
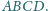 Punkty
Punkty
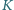 i
i
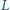 należą
do boku
należą
do boku
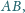 przy czym
przy czym
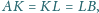 a punkty
a punkty
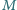 i
i
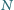 należą do boku
należą do boku
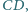 przy czym
przy czym
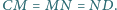 Wykaż,
że
Wykaż,
że
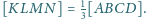
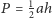
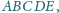 w którym pola trójkątów
w którym pola trójkątów
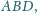
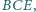
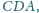
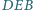 i
i
 są równe.
Udowodnij, że każda przekątna tego pięciokąta jest równoległa do pewnego
jego boku.
są równe.
Udowodnij, że każda przekątna tego pięciokąta jest równoległa do pewnego
jego boku.
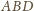 i
i
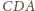 mają wspólną podstawę
mają wspólną podstawę
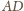 i równe
pola, więc też równe wysokości. Punkty
i równe
pola, więc też równe wysokości. Punkty
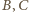 są po tej samej stronie
prostej
są po tej samej stronie
prostej
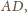 stąd
stąd
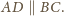 Dla pozostałych przekątnych dowód
jest analogiczny.
Dla pozostałych przekątnych dowód
jest analogiczny.
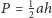
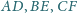 sześciokąta wypukłego
sześciokąta wypukłego
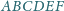 dzieli go na dwa czworokąty o równych polach. Wykaż, że
trójkąty
dzieli go na dwa czworokąty o równych polach. Wykaż, że
trójkąty
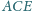 i
i
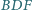 są podobne.
są podobne.
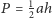
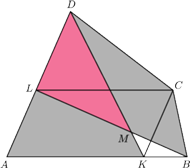
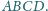 Punkty
Punkty
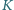 i
i
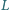 należą
odpowiednio do odcinków
należą
odpowiednio do odcinków
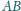 i
i
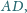 przy czym czworokąt
przy czym czworokąt
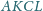 jest równoległobokiem. Odcinki
jest równoległobokiem. Odcinki
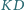 i
i
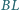 przecinają
się w punkcie
przecinają
się w punkcie
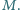 Wykaż, że
Wykaż, że
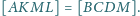
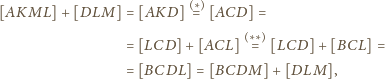
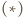 wynika z równoległości
wynika z równoległości
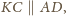 a
a
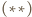 z
z
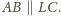
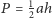
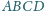 przecinają się w punkcie
przecinają się w punkcie
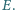 Wyznacz
Wyznacz
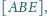 jeśli
jeśli
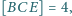
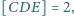
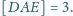
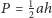
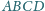 o podstawach
o podstawach
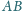 i
i
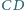 przecinają się
w punkcie
przecinają się
w punkcie
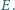 Dane są
Dane są
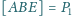 i
i
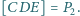 Wyznacz
Wyznacz
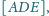
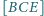 oraz
oraz
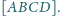
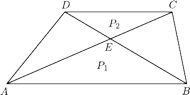
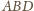 i
i
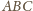 mają wspólną podstawę i równe
wysokości, więc też równe pola. Stąd
mają wspólną podstawę i równe
wysokości, więc też równe pola. Stąd
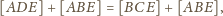
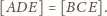
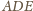 i
i
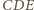 mają wspólną wysokość z
mają wspólną wysokość z
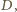 więc
więc
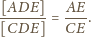
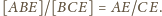 Stąd
Stąd
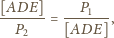
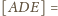
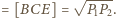 Wobec tego
Wobec tego
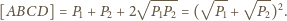
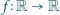 będzie funkcją ściśle rosnącą, odwzorowującą zbiór
wszystkich liczb wymiernych
będzie funkcją ściśle rosnącą, odwzorowującą zbiór
wszystkich liczb wymiernych
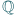 na cały zbiór
na cały zbiór
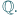 Czy stąd wynika,
że funkcja
Czy stąd wynika,
że funkcja
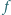 jest przedziałami liniowa (tzn. że
jest przedziałami liniowa (tzn. że
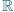 jest sumą
skończenie lub nieskończenie wielu przedziałów dodatniej długości,
o rozłącznych wnętrzach, i w każdym z tych przedziałów
jest sumą
skończenie lub nieskończenie wielu przedziałów dodatniej długości,
o rozłącznych wnętrzach, i w każdym z tych przedziałów
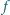 jest
liniowa)?
jest
liniowa)?
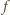 najpierw
w przedziale
najpierw
w przedziale
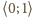 wzorem
wzorem
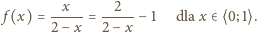
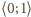 na cały ten przedział; łatwo wyznaczyć funkcję
odwrotną:
na cały ten przedział; łatwo wyznaczyć funkcję
odwrotną:
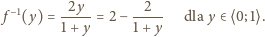
 są liczbami wymiernymi z przedziału
są liczbami wymiernymi z przedziału
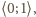 to
to
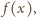
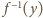 też są liczbami wymiernymi
z przedziału
też są liczbami wymiernymi
z przedziału
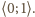 Zatem obrazem zbioru
Zatem obrazem zbioru
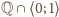 jest
ten sam zbiór.
jest
ten sam zbiór.
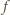 do funkcji
do funkcji
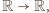 przesuwając jej wykres
o wektor
przesuwając jej wykres
o wektor
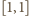 i jego całkowite wielokrotności. Formalnie: przyjmujemy
i jego całkowite wielokrotności. Formalnie: przyjmujemy

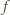 jest ściśle rosnąca; w każdym
z przedziałów
jest ściśle rosnąca; w każdym
z przedziałów
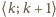 jest ściśle wypukła – więc nie jest liniowa
w żadnym przedziale długości dodatniej. Wreszcie, jest jasne, że obrazem
zbioru
jest ściśle wypukła – więc nie jest liniowa
w żadnym przedziale długości dodatniej. Wreszcie, jest jasne, że obrazem
zbioru
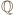 jest cały zbiór
jest cały zbiór
 Wygrywa ten, który pierwszy przekroczy
Wygrywa ten, który pierwszy przekroczy
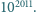 Który
z graczy ma strategię wygrywającą?
Który
z graczy ma strategię wygrywającą?
 i z
i z
 zapałkami. Dwóch graczy
na przemian zabiera z dowolnej kupki liczbę zapałek bedącą dzielnikiem liczby
zapałek w pozostałej kupce. Który z graczy ma strategię wygrywającą?
zapałkami. Dwóch graczy
na przemian zabiera z dowolnej kupki liczbę zapałek bedącą dzielnikiem liczby
zapałek w pozostałej kupce. Który z graczy ma strategię wygrywającą?
 zapałkami?
zapałkami?
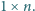 Na jej ostatnich
trzech polach stoi po jednym pionku. Dwóch graczy wykonuje naprzemiennie
ruchy polegające na przestawieniu dowolnego pionka na dowolne wolne pole
bliższe początku planszy. Przegrywa ten, który nie może zrobić ruchu.
Który z graczy ma strategię wygrywającą?
Na jej ostatnich
trzech polach stoi po jednym pionku. Dwóch graczy wykonuje naprzemiennie
ruchy polegające na przestawieniu dowolnego pionka na dowolne wolne pole
bliższe początku planszy. Przegrywa ten, który nie może zrobić ruchu.
Który z graczy ma strategię wygrywającą?
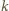 pionków stoi na końcowych polach planszy. Jeżeli zarówno
pionków stoi na końcowych polach planszy. Jeżeli zarówno
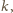 jak i
jak i
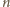 są parzyste, to dzieląc planszę na takie same szufladki
i przestawiając po każdym ruchu pierwszego gracza drugi pionek z szufladki,
w której stał pionek ruszony przez gracza pierwszego, do tej szufladki, do
której pierwszy gracz wstawił pionek, drugi gracz zapewni sobie zwycięstwo.
Jeżeli
są parzyste, to dzieląc planszę na takie same szufladki
i przestawiając po każdym ruchu pierwszego gracza drugi pionek z szufladki,
w której stał pionek ruszony przez gracza pierwszego, do tej szufladki, do
której pierwszy gracz wstawił pionek, drugi gracz zapewni sobie zwycięstwo.
Jeżeli
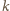 jest parzyste, a
jest parzyste, a
 nieparzyste – pierwszy gracz,
przestawiając ostatni pionek tuż przed pionek pierwszy, sprowadzi grę do
przypadku już rozważonego z sobą w roli drugiego, a więc wygra. Jeżeli
zaś
nieparzyste – pierwszy gracz,
przestawiając ostatni pionek tuż przed pionek pierwszy, sprowadzi grę do
przypadku już rozważonego z sobą w roli drugiego, a więc wygra. Jeżeli
zaś
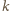 jest nieparzyste, to pierwszy gracz, przestawiając, w zależności
od parzystości
jest nieparzyste, to pierwszy gracz, przestawiając, w zależności
od parzystości
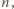 pierwszy bądź ostatni z pionków, zawsze może
sprowadzić grę do przypadku
pierwszy bądź ostatni z pionków, zawsze może
sprowadzić grę do przypadku
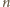 i
i
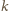 parzystych – a wiec
zawsze wygra.
parzystych – a wiec
zawsze wygra.
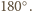
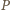 będzie
dowolnym punktem leżącym wewnątrz danego kąta trójściennego, a
będzie
dowolnym punktem leżącym wewnątrz danego kąta trójściennego, a
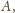
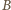 i
i
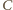 jego rzutami prostokątnymi na płaszczyzny
zawierające ściany danego kąta trójściennego. Jeśli
jego rzutami prostokątnymi na płaszczyzny
zawierające ściany danego kąta trójściennego. Jeśli
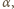
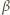 i
i
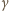 oznaczają miary kątów dwuściennych,
to miary kątów płaskich
oznaczają miary kątów dwuściennych,
to miary kątów płaskich
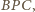
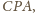
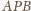 są równe
są równe
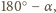
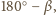
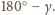
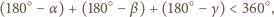
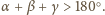
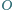 jest środkiem sfery wpisanej w czworościan
jest środkiem sfery wpisanej w czworościan
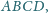 przy czym prosta
przy czym prosta
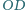 jest prostopadła do krawędzi
jest prostopadła do krawędzi
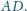 Znaleźć miarę kąta dwuściennego między płaszczyznami
Znaleźć miarę kąta dwuściennego między płaszczyznami
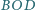 i
i
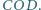
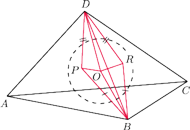
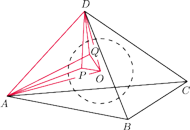
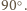 Niech
Niech
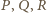 będą
punktami styczności sfery wpisanej odpowiednio ze ścianami
będą
punktami styczności sfery wpisanej odpowiednio ze ścianami
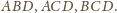 Z równości
Z równości
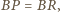
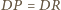 i
i
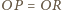 wnioskujemy, że czworościany
wnioskujemy, że czworościany
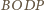 i
i
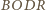 są przystające (
są przystające (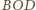 i
i
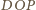 jest równy kątowi dwuściennemu
między płaszczyznami
jest równy kątowi dwuściennemu
między płaszczyznami
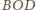 i
i
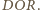 Analogicznie dowodzimy, że
kąt dwuścienny między płaszczyznami
Analogicznie dowodzimy, że
kąt dwuścienny między płaszczyznami
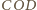 i
i
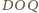 jest
równy kątowi dwuściennemu między płaszczyznami
jest
równy kątowi dwuściennemu między płaszczyznami
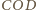 i
i
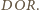 Wykażemy, że punkty
Wykażemy, że punkty
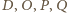 leżą na jednej
płaszczyźnie. Wtedy, korzystając z poprzednich obserwacji, łatwo obliczyć, że
kąt dwuścienny między płaszczyznami
leżą na jednej
płaszczyźnie. Wtedy, korzystając z poprzednich obserwacji, łatwo obliczyć, że
kąt dwuścienny między płaszczyznami
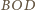 i
i
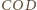 ma miarę
ma miarę
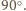
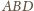 jest prostopadła do prostej
jest prostopadła do prostej
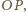 to
to
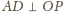 (
(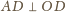 dostajemy
dostajemy
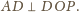 Analogicznie udowodnimy, że
Analogicznie udowodnimy, że
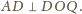 Zatem punkty
Zatem punkty
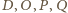 leżą na jednej
płaszczyźnie prostopadłej do krawędzi
leżą na jednej
płaszczyźnie prostopadłej do krawędzi
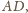 co kończy dowód.
co kończy dowód.
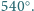
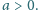 Określamy ciągi
Określamy ciągi
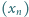 oraz
oraz
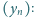
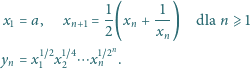
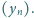
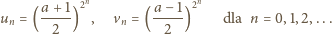
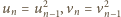 ;
;
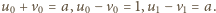
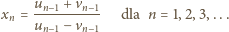
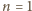 zgadza się. Przyjmijmy jej słuszność dla
zgadza się. Przyjmijmy jej słuszność dla
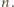 Wtedy dla
Wtedy dla
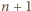 mamy
mamy
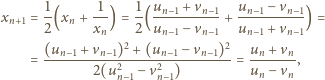
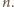 Teraz druga z zapowiedzianych
równości:
Teraz druga z zapowiedzianych
równości:
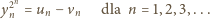
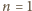 zgadza się. Weźmy
zgadza się. Weźmy
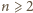 i załóżmy, że
równość analogiczna do (2) zachodzi dla
i załóżmy, że
równość analogiczna do (2) zachodzi dla
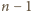 :
:
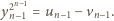
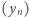 wynika, że
wynika, że
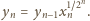 Stąd oraz
z (1):
Stąd oraz
z (1):
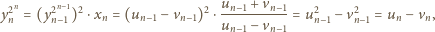
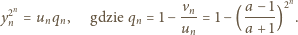
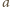 jest dodatnia, więc iloraz w nawiasie jest liczbą o module
mniejszym od 1. Wobec tego
jest dodatnia, więc iloraz w nawiasie jest liczbą o module
mniejszym od 1. Wobec tego
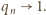 Stąd, ostatecznie,
Stąd, ostatecznie,
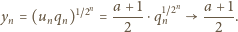
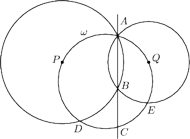
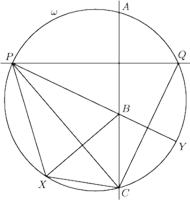
 i
i
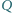 przecinają się w punktach
przecinają się w punktach
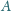 i
i
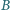 ; promienie
; promienie
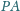 i
i
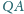 nie są prostopadłe. Okrąg opisany na
trójkącie
nie są prostopadłe. Okrąg opisany na
trójkącie
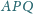 przecina te dwa okręgi w punktach
przecina te dwa okręgi w punktach
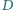 i
i
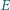 (różnych od
(różnych od
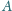 ) oraz przecina prostą
) oraz przecina prostą
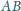 w punkcie
w punkcie
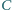 (różnym od
(różnym od
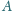 ). Dowieść, że okrąg opisany na trójkącie
). Dowieść, że okrąg opisany na trójkącie
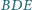 ma środek w punkcie
ma środek w punkcie
 opisany na trójkącie
opisany na trójkącie
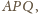 nie jest styczny do żadnego
z dwóch danych okręgów (bo je przecina w punktach różnych od
nie jest styczny do żadnego
z dwóch danych okręgów (bo je przecina w punktach różnych od
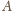 ).
Zatem żaden z odcinków
).
Zatem żaden z odcinków
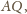
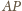 nie jest jego średnicą;
w takim razie żaden z kątów
nie jest jego średnicą;
w takim razie żaden z kątów
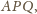
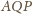 nie jest prosty. Stąd
wniosek, że żaden z punktów
nie jest prosty. Stąd
wniosek, że żaden z punktów
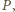
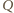 nie leży na prostej
nie leży na prostej
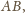 wobec czego prosta
wobec czego prosta
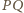 nie przechodzi przez punkt
nie przechodzi przez punkt
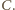
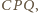 wpisany w okrąg
wpisany w okrąg
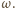 Wysokość poprowadzona z wierzchołka
Wysokość poprowadzona z wierzchołka
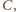 lub jej przedłużenie,
przecina okrąg
lub jej przedłużenie,
przecina okrąg
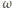 ponownie w punkcie
ponownie w punkcie
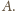 Ortocentrum trójkąta
Ortocentrum trójkąta
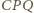 leży w punkcie symetrycznym do
leży w punkcie symetrycznym do
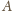 względem prostej
względem prostej
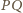 – czyli w punkcie
– czyli w punkcie
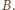
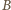 względem boków
względem boków
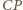 i
i
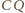 także leżą na okręgu
także leżą na okręgu
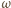 ; oznaczmy je odpowiednio przez
; oznaczmy je odpowiednio przez
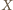 i
i
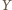 (żaden z nich nie pokrywa się z
(żaden z nich nie pokrywa się z
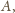 bo punkt
bo punkt
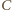 nie leży na prostej
nie leży na prostej
 ).
).
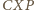 jest symetryczny do
jest symetryczny do
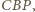 więc
więc
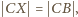
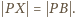 Ostatnia równość mówi, że
Ostatnia równość mówi, że
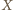 jest punktem okręgu o środku
jest punktem okręgu o środku
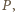 przechodzącego przez
przechodzącego przez
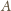 i
i
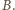 Skoro zaś leży na okręgu
Skoro zaś leży na okręgu
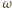 i nie pokrywa się z
i nie pokrywa się z
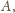 musi się pokrywać z
musi się pokrywać z
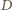 lub
lub
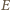 ; ustalmy oznaczenia (
; ustalmy oznaczenia (
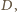
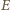 ) tak, że
) tak, że
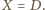 Analogicznie stwierdzamy,
że
Analogicznie stwierdzamy,
że
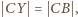
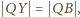
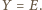 Tak więc
Tak więc
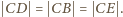 To znaczy, że punkty
To znaczy, że punkty
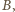
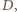
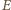 leżą
na okręgu o środku
leżą
na okręgu o środku