- Narzędzia
- Obiekty
- Wielomiany
- Słowa kluczowe
- Kategoria
- Algebra
Matematyka jest jedna: wielomiany mogą wszystko»Zadanie 3
o zadaniu...
- Zadanie pochodzi z artykułu Matematyka jest jedna: wielomiany mogą wszystko
- Publikacja w Delcie: wrzesień 2015
- Publikacja elektroniczna: 31-08-2015
Rozważmy zbiór

złożony z 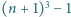 punktów w przestrzeni. Wyznaczyć minimalną liczbę płaszczyzn, których suma mnogościowa zawiera zbiór
punktów w przestrzeni. Wyznaczyć minimalną liczbę płaszczyzn, których suma mnogościowa zawiera zbiór 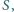 ale nie zawiera punktu
ale nie zawiera punktu 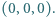
Rozwiązanie
Zauważmy, że 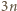 płaszczyzn o równaniach
płaszczyzn o równaniach  dla
dla 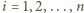 spełnia żądany warunek. Wykażemy, że
spełnia żądany warunek. Wykażemy, że 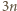 jest minimalną liczbą o tej własności.
jest minimalną liczbą o tej własności.
Załóżmy więc, że suma mnogościowa pewnych 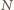 płaszczyzn danych równaniami
płaszczyzn danych równaniami

pokrywa zbiór 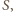 ale nie zawiera punktu
ale nie zawiera punktu 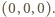 Rozważmy wielomian trzech zmiennych
Rozważmy wielomian trzech zmiennych  dany jako
dany jako

Jest to wielomian łącznego stopnia  który spełnia warunek
który spełnia warunek 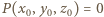 dla
dla 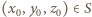 oraz
oraz 
Za pomocą wielomianu 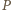 udało się nam przetłumaczyć kombinatoryczny warunek dotyczący płaszczyzn na język algebry. Dzięki temu możemy wykorzystać jej narzędzia, zapominając o kombinatorycznej naturze zadania.
udało się nam przetłumaczyć kombinatoryczny warunek dotyczący płaszczyzn na język algebry. Dzięki temu możemy wykorzystać jej narzędzia, zapominając o kombinatorycznej naturze zadania.
Dla dowolnego wielomianu trzech zmiennych  określmy operację
określmy operację 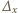 zdefiniowaną jako
zdefiniowaną jako

W analogiczny sposób definiujemy operację 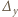 oraz
oraz 
Za pomocą nietrudnego rachunku na współczynnikach sprawdzimy najpierw, że operacja 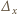 zmniejsza łączny stopień wielomianu co najmniej o
zmniejsza łączny stopień wielomianu co najmniej o 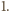 Załóżmy bowiem, że stopień pewnego wielomianu
Załóżmy bowiem, że stopień pewnego wielomianu 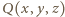 to
to 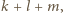 przy czym w rozwinięciu
przy czym w rozwinięciu 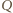 pojawia się jednomian postaci
pojawia się jednomian postaci 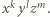 Korzystając ze wzoru dwumianowego Newtona, uzyskujemy
Korzystając ze wzoru dwumianowego Newtona, uzyskujemy

Otrzymaliśmy więc sumę jednomianów o łącznym stopniu nieprzekraczającym 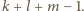 Stosując to samo rozumowanie do każdego jednomianu postaci
Stosując to samo rozumowanie do każdego jednomianu postaci 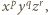 który pojawia się w rozwinięciu
który pojawia się w rozwinięciu 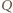 i spełnia
i spełnia 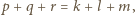 widzimy, że operacja
widzimy, że operacja 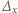 redukuje wszystkie jednomiany o łącznym stopniu
redukuje wszystkie jednomiany o łącznym stopniu 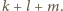 Potwierdza to nasze stwierdzenie.
Potwierdza to nasze stwierdzenie.
Zauważmy, że skoro wielomian 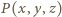 zeruje się dla dowolnej trójki
zeruje się dla dowolnej trójki 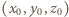 spełniającej
spełniającej 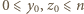 oraz
oraz 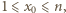 to
to 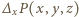 zeruje się dla dowolnej trójki
zeruje się dla dowolnej trójki 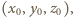 która spełnia
która spełnia 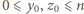 oraz
oraz 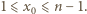 Jednocześnie, mamy
Jednocześnie, mamy

Powtarzając operację 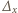 aż
aż 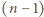 -krotnie, otrzymujemy wielomian
-krotnie, otrzymujemy wielomian 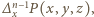 który zeruje się dla dowolnej trójki postaci
który zeruje się dla dowolnej trójki postaci 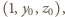 gdzie
gdzie 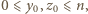 oraz nie zeruje się dla
oraz nie zeruje się dla 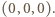 Używając więc operacji
Używając więc operacji 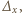 już ostatni raz dostajemy
już ostatni raz dostajemy

Wielomian, który otrzymaliśmy z wielomianu 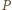 po
po  -krotnym zastosowaniu operacji
-krotnym zastosowaniu operacji 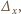 nie zeruje się więc w punkcie
nie zeruje się więc w punkcie 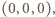 ale zeruje się dla dowolnego punktu postaci
ale zeruje się dla dowolnego punktu postaci 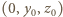 gdzie
gdzie 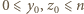 i co najmniej jedna z liczb
i co najmniej jedna z liczb 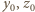 jest różna od zera.
jest różna od zera.
Możemy zatem powtórzyć cały powyższy proces, tym razem względem zmiennej 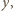 startując od wielomianu otrzymanego w ostatnim kroku. Wielomian
startując od wielomianu otrzymanego w ostatnim kroku. Wielomian 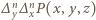 zeruje się więc dla dowolnej trójki postaci
zeruje się więc dla dowolnej trójki postaci 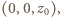 gdzie
gdzie 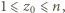 ale nie dla trójki
ale nie dla trójki  Ostatecznie już, rozumując w ten sam sposób względem zmiennej
Ostatecznie już, rozumując w ten sam sposób względem zmiennej 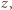 dochodzimy do wniosku, że wielomian
dochodzimy do wniosku, że wielomian 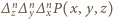 nie zeruje się w punkcie
nie zeruje się w punkcie 
Nie jest to zatem wielomian zerowy. Wcześniej udowodniliśmy jednak, że dowolna z operacji 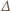 redukuje łączny stopień wielomianu co najmniej o
redukuje łączny stopień wielomianu co najmniej o 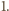 Stopień wielomianu
Stopień wielomianu 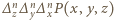 nie przekracza zatem
nie przekracza zatem  Stąd
Stąd 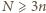 i rozwiązanie zadania jest zakończone.
i rozwiązanie zadania jest zakończone.
 oraz
oraz 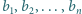 będą dwoma różnymi (czyli różniącymi się nie tylko porządkiem) zestawami liczb całkowitych dodatnich. Udowodnić, że jeżeli zestaw liczb postaci
będą dwoma różnymi (czyli różniącymi się nie tylko porządkiem) zestawami liczb całkowitych dodatnich. Udowodnić, że jeżeli zestaw liczb postaci 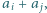 gdzie
gdzie 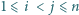 pokrywa się z zestawem
pokrywa się z zestawem 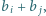 dla
dla 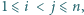 to
to 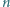 jest potęgą liczby 2.
jest potęgą liczby 2.
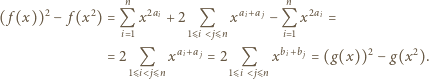
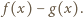 Nie jest to wielomian zerowy oraz
Nie jest to wielomian zerowy oraz 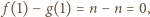 a więc liczba
a więc liczba 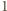 jest jego pierwiastkiem. Oznaczmy przez
jest jego pierwiastkiem. Oznaczmy przez 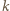 krotność owego pierwiastka, czyli
krotność owego pierwiastka, czyli 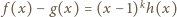 dla pewnego wielomianu
dla pewnego wielomianu  takiego, że
takiego, że  Wówczas
Wówczas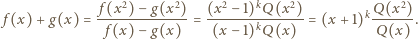
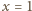 w powyższej równości, dostajemy
w powyższej równości, dostajemy
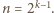
 spełniają warunki
spełniają warunki

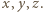
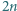 parami różnych liczb rzeczywistych
parami różnych liczb rzeczywistych  oraz tablica
oraz tablica  W pole leżące w
W pole leżące w 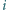 -tym wierszu i w
-tym wierszu i w 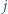 -tej kolumnie wpisano liczbę
-tej kolumnie wpisano liczbę 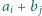 dla
dla 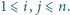 Udowodnić, że jeżeli iloczyny liczb we wszystkich kolumnach są równe, to również iloczyny liczb we wszystkich wierszach są równe.
Udowodnić, że jeżeli iloczyny liczb we wszystkich kolumnach są równe, to również iloczyny liczb we wszystkich wierszach są równe.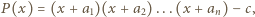 gdzie
gdzie  jest wartością wspólną iloczynów liczb w kolumnach.
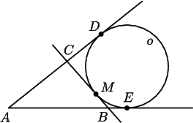
jest wartością wspólną iloczynów liczb w kolumnach.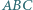 jest styczny do boków
jest styczny do boków 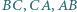 odpowiednio w punktach
odpowiednio w punktach 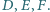 Prosta równoległa do
Prosta równoległa do 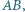 przechodząca przez punkt
przechodząca przez punkt 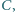 przecina proste
przecina proste 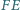 i
i 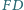 odpowiednio w punktach
odpowiednio w punktach 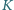 i
i  Udowodnij, że na czworokącie
Udowodnij, że na czworokącie  można opisać okrąg.
można opisać okrąg.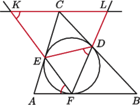
 i
i 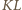 oraz z twierdzenia (*) uzyskujemy
oraz z twierdzenia (*) uzyskujemy 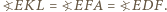 Stąd
Stąd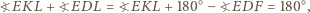
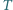 jest wpisany w okrąg
jest wpisany w okrąg 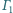 oraz opisany na okręgu
oraz opisany na okręgu 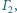 przy czym
przy czym  są kolejnymi punktami styczności
są kolejnymi punktami styczności 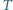 z
z 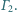 Wykaż, że
Wykaż, że 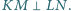

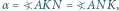
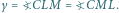
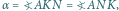
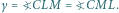
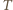 jest wpisany w okrąg, to
jest wpisany w okrąg, to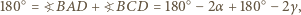
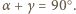
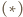 dla okręgu
dla okręgu 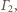 mamy
mamy 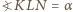 oraz
oraz 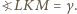 Wobec tego
Wobec tego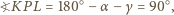
 i taki punkt
i taki punkt  w jego wnętrzu, dla którego
w jego wnętrzu, dla którego  Wyznacz
Wyznacz 
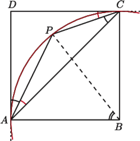
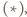 prosta
prosta 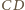 jest styczna do okręgu opisanego na trójkącie
jest styczna do okręgu opisanego na trójkącie  Wobec tego środek tego okręgu leży na prostej
Wobec tego środek tego okręgu leży na prostej 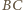 (bo
(bo 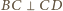 ). Analogicznie prosta
). Analogicznie prosta  także jest styczna do tego okręgu, gdyż
także jest styczna do tego okręgu, gdyż 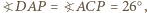 zatem środek rozważanego okręgu leży też na prostej
zatem środek rozważanego okręgu leży też na prostej 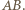 Stąd jest nim punkt
Stąd jest nim punkt 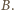
 jest więc kątem środkowym opartym na tym samym łuku, co kąt wpisany
jest więc kątem środkowym opartym na tym samym łuku, co kąt wpisany 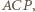 zatem
zatem 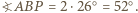
 wpisany w trójkąt
wpisany w trójkąt  jest styczny do boków
jest styczny do boków 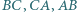 odpowiednio w punktach
odpowiednio w punktach 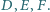 Wykaż, że środki
Wykaż, że środki  okręgów wpisanych w trójkąty
okręgów wpisanych w trójkąty 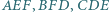 leżą na okręgu
leżą na okręgu 
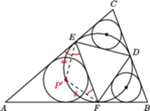
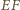 okręgu
okręgu 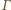 przez
przez  Wówczas
Wówczas 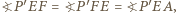 przy czym druga równość wynika z twierdzenia
przy czym druga równość wynika z twierdzenia 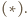 Wobec tego
Wobec tego 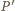 leży na dwusiecznej kąta
leży na dwusiecznej kąta  Analogicznie dla kąta
Analogicznie dla kąta 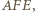 więc
więc  Dowód dla punktów
Dowód dla punktów 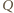 i
i 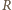 przebiega podobnie.
przebiega podobnie.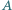 i
i 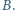 Proste styczne do tych okręgów w punkcie
Proste styczne do tych okręgów w punkcie 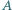 przecinają je w drugich punktach
przecinają je w drugich punktach 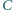 i
i 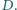 Wykaż, że
Wykaż, że 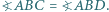
 poprowadzono prostą przecinającą dany okrąg
poprowadzono prostą przecinającą dany okrąg 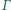 w punktach
w punktach 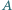 i
i 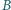 oraz prostą styczną do
oraz prostą styczną do 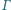 w punkcie
w punkcie 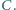 Wykaż, że
Wykaż, że 
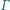 jest styczny do prostej
jest styczny do prostej 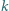 w punkcie
w punkcie 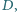 cięciwa
cięciwa 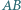 tego okręgu jest równoległa do
tego okręgu jest równoległa do  punkt
punkt 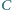 należy do prostej
należy do prostej 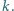 Proste
Proste 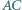 i
i 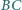 przecinają okrąg
przecinają okrąg 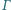 w drugich punktach
w drugich punktach 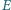 i
i 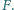 Wykaż, że prosta
Wykaż, że prosta 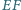 przechodzi przez środek odcinka
przechodzi przez środek odcinka 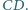
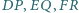 przecinają się w jednym punkcie
przecinają się w jednym punkcie  oraz że punkty
oraz że punkty 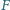 i
i  są symetryczne względem prostej
są symetryczne względem prostej 
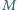 leżący we wnętrzu kąta o wierzchołku
leżący we wnętrzu kąta o wierzchołku 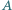 poprowadzić prostą, która, przecinając ramiona kąta w punktach
poprowadzić prostą, która, przecinając ramiona kąta w punktach 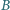 i
i 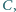 wyznacza trójkąt
wyznacza trójkąt 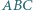 o najmniejszym polu.
o najmniejszym polu.

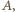 a jego przekątne przecinają się w punkcie
a jego przekątne przecinają się w punkcie 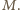 Przekątna tego równoległoboku, która przecina ramiona kąta (w punktach
Przekątna tego równoległoboku, która przecina ramiona kąta (w punktach  i
i 
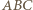 o najmniejszym polu.
o najmniejszym polu. jest inną prostą przechodzącą przez punkt
jest inną prostą przechodzącą przez punkt 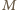 (na przykład taką, że
(na przykład taką, że 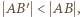
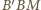 i
i  mamy:
mamy: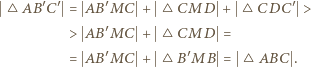
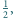 a minimalne pole trójkąta zawierającego kwadrat jednostkowy jest równe 2.
a minimalne pole trójkąta zawierającego kwadrat jednostkowy jest równe 2. i w nim trójkąt
i w nim trójkąt 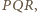 którego wierzchołki leżą na różnych bokach kwadratu tak, że
którego wierzchołki leżą na różnych bokach kwadratu tak, że 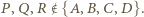 Wówczas trójkąt
Wówczas trójkąt 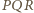 łatwo zastąpić trójkątem o większej wysokości, czyli większym polu (
łatwo zastąpić trójkątem o większej wysokości, czyli większym polu (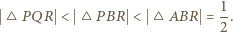


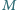 leżący we wnętrzu kąta o wierzchołku
leżący we wnętrzu kąta o wierzchołku  poprowadzić prostą, która, przecinając ramiona kąta w punktach
poprowadzić prostą, która, przecinając ramiona kąta w punktach 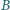 i
i 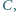 wyznacza trójkąt
wyznacza trójkąt 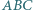 o najmniejszym obwodzie.
o najmniejszym obwodzie. wpisujemy dwa okręgi przechodzące przez punkt
wpisujemy dwa okręgi przechodzące przez punkt 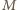 (
(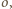 w punkcie
w punkcie  wyznaczamy styczną, która przecina ramiona kąta w punktach
wyznaczamy styczną, która przecina ramiona kąta w punktach 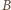 i
i 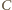 (
(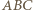 spełnia warunki zadania i ma najmniejszy obwód równy
spełnia warunki zadania i ma najmniejszy obwód równy 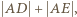 gdzie
gdzie 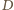 i
i 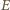 to punkty styczności okręgu
to punkty styczności okręgu  z ramionami kąta (jest tak, bo
z ramionami kąta (jest tak, bo 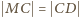 i
i 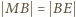 ).
).
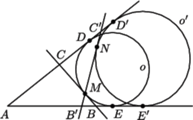
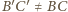 jest inną prostą zawierającą punkt
jest inną prostą zawierającą punkt 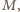 to okrąg
to okrąg 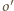 dopisany do trójkąta
dopisany do trójkąta 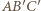 jest styczny do ramion kąta w punktach
jest styczny do ramion kąta w punktach 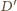 i
i 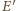 oraz do odcinka
oraz do odcinka 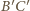 w punkcie
w punkcie 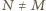 (
(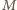 leży na zewnątrz okręgu dopisanego
leży na zewnątrz okręgu dopisanego 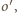 więc okrąg
więc okrąg  ma większy promień niż okrąg
ma większy promień niż okrąg  i obwód trójkąta
i obwód trójkąta  jest równy
jest równy 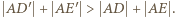
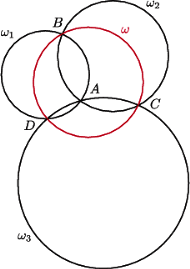
 Wówczas istnieją w tym zbiorze okręgi
Wówczas istnieją w tym zbiorze okręgi 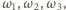 które mają punkt wspólny
które mają punkt wspólny 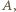 oraz okrąg
oraz okrąg  który nie przechodzi przez
który nie przechodzi przez  Oznaczmy punkty wspólne, różne od
Oznaczmy punkty wspólne, różne od 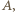 okręgów
okręgów 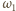 i
i 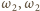 i
i 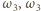 i
i 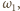 odpowiednio przez
odpowiednio przez  oraz
oraz  Wówczas
Wówczas 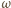 przechodzi przez wszystkie te punkty.
przechodzi przez wszystkie te punkty.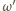 ze zbioru
ze zbioru  Musi on przechodzić przez
Musi on przechodzić przez  lub
lub 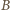 (ponieważ są to jedyne punkty wspólne okręgów
(ponieważ są to jedyne punkty wspólne okręgów 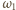 i
i  ). Podobnie okrąg
). Podobnie okrąg  musi przechodzić przez co najmniej jeden z każdej pary punktów spośród
musi przechodzić przez co najmniej jeden z każdej pary punktów spośród 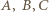 i
i 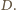 Stąd
Stąd  przechodzi przez co najmniej trzy z tych punktów. To jest jednak niemożliwe, bo każda taka trójka wyznacza jednoznacznie jeden z okręgów
przechodzi przez co najmniej trzy z tych punktów. To jest jednak niemożliwe, bo każda taka trójka wyznacza jednoznacznie jeden z okręgów 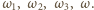
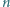 oraz liczb rzeczywistych
oraz liczb rzeczywistych  spełniających
spełniających 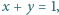 prawdziwa jest tożsamość
prawdziwa jest tożsamość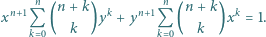
![x ∈[0,1]](/math/temat/matematyka/analiza/zadania/2015/06/29/zm-1463/1x-334d5fb9c059ea46c340b1dc0cd157b4566f8db6-im-66,57,43-FF,FF,FF.gif) i rozważmy doświadczenie losowe polegające na rzucaniu monetą tak długo, dopóki
i rozważmy doświadczenie losowe polegające na rzucaniu monetą tak długo, dopóki 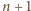 razy wypadnie orzeł lub
razy wypadnie orzeł lub  razy reszka. Prawdopodobieństwo wypadnięcia orła w pojedynczym rzucie wynosi
razy reszka. Prawdopodobieństwo wypadnięcia orła w pojedynczym rzucie wynosi 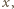 zaś reszki
zaś reszki 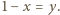 Zauważmy, że prawdopodobieństwo tego, że doświadczenie zakończy się w rzucie
Zauważmy, że prawdopodobieństwo tego, że doświadczenie zakończy się w rzucie 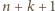 (dla
(dla 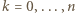 ) z powodu wypadnięcia
) z powodu wypadnięcia 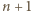 orłów wynosi
orłów wynosi  a z powodu wypadnięcia
a z powodu wypadnięcia 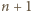 reszek -
reszek - 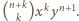 Sumując prawdopodobieństwa poszczególnych możliwości zakończenia doświadczenia, otrzymujemy
Sumując prawdopodobieństwa poszczególnych możliwości zakończenia doświadczenia, otrzymujemy
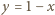 lewa strona tożsamości jest wielomianem zmiennej
lewa strona tożsamości jest wielomianem zmiennej 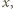 który jest tożsamościowo równy
który jest tożsamościowo równy 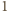 na przedziale
na przedziale ![|[0,1],](/math/temat/matematyka/analiza/zadania/2015/06/29/zm-1463/16x-334d5fb9c059ea46c340b1dc0cd157b4566f8db6-im-66,57,43-FF,FF,FF.gif) więc jest on równy
więc jest on równy 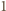 dla wszystkich
dla wszystkich 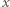 rzeczywistych.
rzeczywistych.