Łuki Talesa»Zadanie 7
o zadaniu...
- Zadanie pochodzi z artykułu Łuki Talesa
- Publikacja w Delcie: wrzesień 2017
- Publikacja elektroniczna: 1 września 2017
Udowodnij stwierdzenia z drugiego akapitu niniejszego artykułu.
Udowodnij stwierdzenia z drugiego akapitu niniejszego artykułu.
Największy wspólny dzielnik liczb całkowitych dodatnich 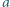 i
i 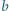 jest równy
jest równy 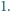 Dowieść, że największy wspólny dzielnik liczb
Dowieść, że największy wspólny dzielnik liczb 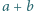 i
i 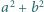 nie przekracza
nie przekracza 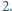
Liczby dodatnie 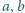 spełniają warunek
spełniają warunek 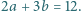 Wykazać, że dla każdej liczby naturalnej
Wykazać, że dla każdej liczby naturalnej 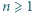 zachodzi nierówność
zachodzi nierówność
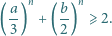
Wyznaczyć zbiór tych liczb wymiernych dodatnich, które można przedstawić w postaci ułamka  dla pewnych liczb naturalnych
dla pewnych liczb naturalnych 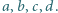
Zadanie 504 zaproponował pan Paweł Najman z Jaworzna.
Gra: odgadywanie liczby. Przeciwnik wybiera liczbę ze zbioru 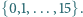 Mamy prawo zadać 7 pytań, oczekując odpowiedzi Tak lub Nie. Przeciwnik na wszystkie pytania odpowiada; wolno mu przy tym skłamać, ale co najwyżej jeden raz. Podać taktykę gwarantującą prawidłowe rozpoznanie wybranej liczby.
Mamy prawo zadać 7 pytań, oczekując odpowiedzi Tak lub Nie. Przeciwnik na wszystkie pytania odpowiada; wolno mu przy tym skłamać, ale co najwyżej jeden raz. Podać taktykę gwarantującą prawidłowe rozpoznanie wybranej liczby.
Wyznaczyć najmniejszą liczbę dodatnią 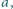 dla której zachodzi implikacja:
dla której zachodzi implikacja:
Jeżeli funkcja 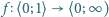 spełnia warunki
spełnia warunki 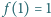 oraz
oraz
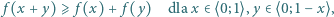
to 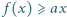 dla
dla 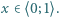
Niech 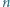 będzie liczbą naturalną większą od 4. Udowodnić, że w elipsę o półosiach różnej długości nie można wpisać
będzie liczbą naturalną większą od 4. Udowodnić, że w elipsę o półosiach różnej długości nie można wpisać 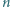 -kąta foremnego.
-kąta foremnego.
Znaleźć największą liczbę naturalną 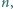 dla której
dla której 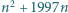 jest kwadratem liczby naturalnej.
jest kwadratem liczby naturalnej.
W dwa trójkąty, o bokach odpowiednio 17, 25, 26 i 17, 25, 28, wpisujemy koła. Które z wpisanych kół ma większy promień?
Zadanie 352 (nawiązujące do zadania 308 z numeru 10/1995) zaproponował pan Andrzej Daniluk z Krakowa.
Funkcja różniczkowalna 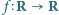 spełnia wraz z pewną funkcją
spełnia wraz z pewną funkcją 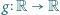 równanie
równanie 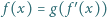 dla
dla 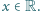 Dowieść, że funkcja
Dowieść, że funkcja 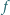 jest wypukła lub wklęsła.
jest wypukła lub wklęsła.
Wyznaczyć największą liczbę naturalną 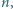 dla której istnieją czteroelementowe zbiory
dla której istnieją czteroelementowe zbiory 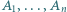 o następującej własności: każdy zbiór
o następującej własności: każdy zbiór 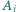 ma z każdym innym zbiorem
ma z każdym innym zbiorem 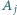 dokładnie jeden element wspólny, ale nie istnieje wspólny element wszystkich zbiorów
dokładnie jeden element wspólny, ale nie istnieje wspólny element wszystkich zbiorów 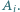
Dana jest liczba 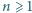 oraz pewien zbiór
oraz pewien zbiór 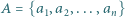 dodatnich liczb całkowitych. Na okręgu wyróżniono
dodatnich liczb całkowitych. Na okręgu wyróżniono 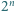 punktów i każdemu z nich przyporządkowano jedną z liczb ze zbioru
punktów i każdemu z nich przyporządkowano jedną z liczb ze zbioru 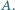 Udowodnić, że iloczyn liczb znajdujących się na pewnym łuku tego okręgu jest kwadratem liczby całkowitej.
Udowodnić, że iloczyn liczb znajdujących się na pewnym łuku tego okręgu jest kwadratem liczby całkowitej.
Niech 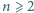 będzie liczbą całkowitą. Znaleźć liczbę przedstawień liczby
będzie liczbą całkowitą. Znaleźć liczbę przedstawień liczby 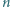 w postaci sumy pewnej liczby dodatnich całkowitych składników, pośród których jest parzysta liczba liczb parzystych.
w postaci sumy pewnej liczby dodatnich całkowitych składników, pośród których jest parzysta liczba liczb parzystych.
Dwa okręgi, styczne zewnętrznie w punkcie 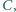 są styczne do prostej
są styczne do prostej 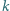 w punktach
w punktach 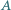 i
i 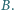 Wykaż, że trójkąt
Wykaż, że trójkąt 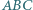 jest prostokątny.
jest prostokątny.
Wykaż, że jeżeli przekątne pewnego trapezu są prostopadłe, to suma długości podstaw tego trapezu jest nie większa od sumy długości jego ramion.
Wewnątrz kwadratu 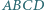 wybrano taki punkt
wybrano taki punkt 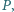 że
że 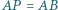 oraz
oraz 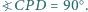 Wykaż, że
Wykaż, że 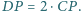
W trójkącie 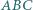 środkowe poprowadzone z wierzchołków
środkowe poprowadzone z wierzchołków 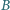 i
i 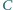 są prostopadłe oraz
są prostopadłe oraz 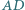 jest wysokością. Wykaż, że
jest wysokością. Wykaż, że 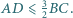
Okrąg wpisany w trójkąt 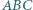 jest styczny do boków
jest styczny do boków 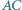 i
i 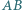 odpowiednio w punktach
odpowiednio w punktach 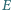 i
i 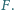 Punkt
Punkt 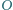 jest środkiem tego okręgu, a punkt
jest środkiem tego okręgu, a punkt 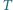 jest symetryczny do punktu
jest symetryczny do punktu 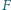 względem punktu
względem punktu 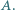 Wykaż, że proste
Wykaż, że proste 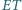 i
i 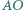 są równoległe.
są równoległe.