Niech
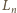 oznacza sumę po lewej stronie zależności, podanej
na początku zadania, zaś
oznacza sumę po lewej stronie zależności, podanej
na początku zadania, zaś
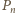 – ułamek po prawej stronie. Dla
– ułamek po prawej stronie. Dla
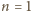 mamy
mamy
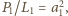 zatem równość
zatem równość
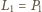 wymusza
wartość
wymusza
wartość
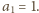 Dalej,
Dalej,
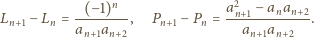
Widać więc, że podana zależność jest spełniona dla wszystkich
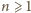 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
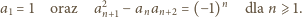 | (1) |
Jeżeli ciąg
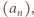 spełniający ten warunek, miałby również spełniać
rekurencję typu
spełniający ten warunek, miałby również spełniać
rekurencję typu
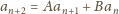 | (2) |
(z
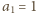 ), to dla
), to dla
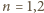 mielibyśmy
mielibyśmy

Pierwsza para równości to układ równań liniowych (z niewiadomymi
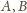 ) o wyznaczniku
) o wyznaczniku
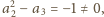 więc mający dokładnie
jedno rozwiązanie. Przy tym jest on spełniony dla
więc mający dokładnie
jedno rozwiązanie. Przy tym jest on spełniony dla
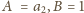 (co łatwo
stwierdzić, korzystając z drugiej pary równości). Stąd wniosek, że
jedynym kandydatem na postulowaną zależność rekurencyjną jest
równanie
(co łatwo
stwierdzić, korzystając z drugiej pary równości). Stąd wniosek, że
jedynym kandydatem na postulowaną zależność rekurencyjną jest
równanie
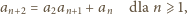 | (3) |
z warunkiem początkowym
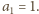 Wprowadźmy oznaczenia:
Wprowadźmy oznaczenia:
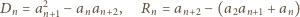
i zauważmy, że (dla
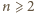 )
)
skąd przez odjęcie stronami
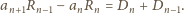 | (4) |
Ponadto (wobec
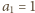 ) mamy:
) mamy:
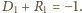
Wnioski: Jeżeli ciąg liczb całkowitych dodatnich
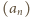 spełnia
wyjściową zależność, czyli warunki (1), to dla wszystkich
spełnia
wyjściową zależność, czyli warunki (1), to dla wszystkich
 mamy
mamy
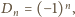 więc prawa strona (4) ma stale wartość 0; przy tym
więc prawa strona (4) ma stale wartość 0; przy tym
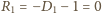 i ze wzoru (4) wynika, że
i ze wzoru (4) wynika, że
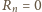 dla wszystkich
dla wszystkich
 – mamy zależność (3).
– mamy zależność (3).
Na odwrót, jeśli równanie (3) (z wyrazem początkowym
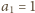 oraz
dowolnym
oraz
dowolnym
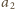 ) jest dla wszystkich
) jest dla wszystkich
 spełnione, czyli wszystkie
spełnione, czyli wszystkie
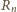 są zerami, to wobec (4):
są zerami, to wobec (4):
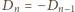 dla
dla
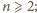 przy tym
przy tym
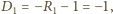 zatem
zatem
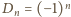 – a to jest zależność
(1).
– a to jest zależność
(1).
Ostatecznie więc, zadana na wstępie zależność jest równoważna rekurencji
liniowej (2) z parametrami
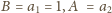 – dowolna liczba
naturalna.
– dowolna liczba
naturalna.
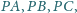 jeśli
jeśli
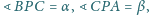
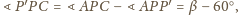 podobnie
podobnie
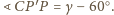 Stąd, korzystając z równości
Stąd, korzystając z równości
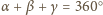 i z sumy
miar kątów trójkąta
i z sumy
miar kątów trójkąta
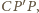 otrzymujemy
otrzymujemy
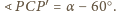
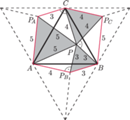
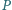 leży wewnątrz trójkąta równobocznego
leży wewnątrz trójkąta równobocznego
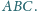 Wyznacz
pole trójkąta
Wyznacz
pole trójkąta
 jeśli
jeśli
 wokół wierzchołka
wokół wierzchołka
 Niech
Niech
 będzie
obrazem punktu
będzie
obrazem punktu
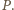 Trójkąt
Trójkąt
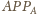 jest równoboczny. Trójkąt
jest równoboczny. Trójkąt
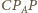 ma boki długości
ma boki długości
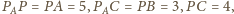 więc
jest prostokątny.
więc
jest prostokątny.
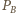 i
i
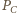 jako obrazy
jako obrazy
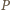 przy obrotach wokół odpowiednio wierzchołków
przy obrotach wokół odpowiednio wierzchołków
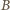 i
i
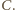 Wtedy trójkąty
Wtedy trójkąty
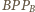 i
i
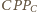 są równoboczne o bokach
odpowiednio długości 3 i 4, a trójkąty
są równoboczne o bokach
odpowiednio długości 3 i 4, a trójkąty
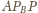 i
i
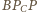 oba są
prostokątne o bokach długości 3, 4, 5.
oba są
prostokątne o bokach długości 3, 4, 5.
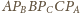 jest równe
jest równe
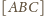 plus
„dodatki”:
plus
„dodatki”:
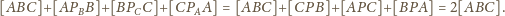
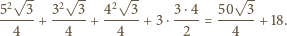
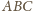 jest więc dwukrotnie mniejsze:
jest więc dwukrotnie mniejsze:
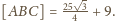
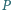 leży wewnątrz trójkąta równobocznego
leży wewnątrz trójkąta równobocznego
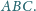 Udowodnij, że
Udowodnij, że
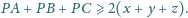
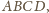 w którym
w którym
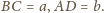 Na krawędziach
Na krawędziach
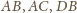 i
i
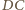 wybierzmy
odpowiednio takie punkty
wybierzmy
odpowiednio takie punkty
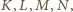 że
że
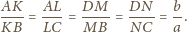
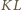 i
i
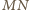 są równoległe. Wobec tego punkty
są równoległe. Wobec tego punkty
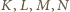 leżą na
jednej płaszczyźnie. Ponadto z twierdzenia Talesa obliczamy
leżą na
jednej płaszczyźnie. Ponadto z twierdzenia Talesa obliczamy
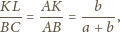
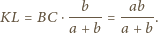
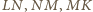 ma
długość
ma
długość
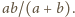 Stąd wniosek, że czworokąt
Stąd wniosek, że czworokąt
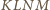 jest
rombem.
jest
rombem.
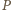 będzie środkiem rombu
będzie środkiem rombu
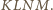 Punkty przecięcia
prostych, zawierających dwusieczne kątów
Punkty przecięcia
prostych, zawierających dwusieczne kątów
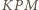 i
i
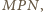 z bokami
rombu tworzą wierzchołki czworokąta. Czworokąt ten jest kwadratem, gdyż jego
przekątne są równe i przecinają się pod kątem prostym.
z bokami
rombu tworzą wierzchołki czworokąta. Czworokąt ten jest kwadratem, gdyż jego
przekątne są równe i przecinają się pod kątem prostym.
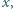 dla których liczby
dla których liczby
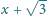 oraz
oraz
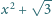 są wymierne.
są wymierne.
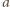 i
i
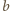 odpowiednio liczby wymierne
odpowiednio liczby wymierne
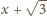 oraz
oraz
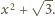 Wówczas
Wówczas
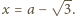 Stąd
otrzymujemy
Stąd
otrzymujemy
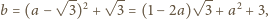
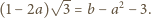
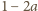 jest różna od zera. Wówczas
jest różna od zera. Wówczas
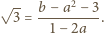
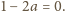 Wobec tego
Wobec tego
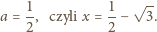
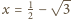 spełnia warunki
zadania. Na mocy powyższego rozumowania jest to jedyna liczba o żądanej
własności.
spełnia warunki
zadania. Na mocy powyższego rozumowania jest to jedyna liczba o żądanej
własności.
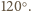 Podnosząc w przestrzeni ten punkt
nieznacznie do góry, skonstruujemy odpowiedni czworościan.
Podnosząc w przestrzeni ten punkt
nieznacznie do góry, skonstruujemy odpowiedni czworościan.
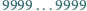 jest zapisana za pomocą
jest zapisana za pomocą
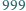 dziewiątek. Ile
wynosi suma cyfr kwadratu tej liczby?
dziewiątek. Ile
wynosi suma cyfr kwadratu tej liczby?
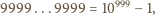
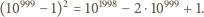
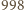 dziewiątek, a potem już prawie same zera
dziewiątek, a potem już prawie same zera
 Wychodzi
Wychodzi
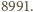
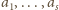 to będą liczby tych, którzy uścisnęli dłonie – odpowiednio –
to będą liczby tych, którzy uścisnęli dłonie – odpowiednio –
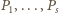 osobom, natomiast
osobom, natomiast
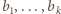 – liczby tych, którzy
uścisnęli dłonie
– liczby tych, którzy
uścisnęli dłonie
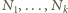 osobom, przy czym
osobom, przy czym
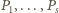 to liczby
parzyste,
to liczby
parzyste,
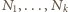 zaś – nieparzyste. Podwojona suma wszystkich
uścisków to
zaś – nieparzyste. Podwojona suma wszystkich
uścisków to
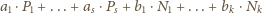
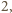 więc
więc
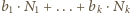 też
jest podzielna przez
też
jest podzielna przez
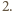 Interesuje nas suma
Interesuje nas suma
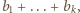 która
również jest liczbą parzystą, bo parzystość liczby
która
również jest liczbą parzystą, bo parzystość liczby
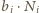 jest dla
każdego
jest dla
każdego
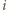 taka sama, jak parzystość
taka sama, jak parzystość
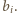
 Ala i Bartek grają w grę,
wykonując ruchy na przemian. Stan gry jest liczbą całkowitą i zmienia swą
wartość w trakcie gry. Gracz, do którego należy ruch, może do tej
liczby zastosować jedną z dwóch operacji: odjąć od niej dowolną
dodatnią liczbę całkowitą, mniejszą niż
Ala i Bartek grają w grę,
wykonując ruchy na przemian. Stan gry jest liczbą całkowitą i zmienia swą
wartość w trakcie gry. Gracz, do którego należy ruch, może do tej
liczby zastosować jedną z dwóch operacji: odjąć od niej dowolną
dodatnią liczbę całkowitą, mniejszą niż
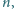 albo podzielić ją przez
albo podzielić ją przez
 i zaokrąglić wynik do najbliższej liczby całkowitej (wobec
nieparzystości
i zaokrąglić wynik do najbliższej liczby całkowitej (wobec
nieparzystości
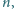 kierunek zaokrąglenia jest zawsze dobrze określony).
Powstała nowa wartość przechodzi do dyspozycji przeciwnika. Wygrywa,
kto pierwszy uzyska wartość 0. Rozpoczyna Ala, startując od liczby
kierunek zaokrąglenia jest zawsze dobrze określony).
Powstała nowa wartość przechodzi do dyspozycji przeciwnika. Wygrywa,
kto pierwszy uzyska wartość 0. Rozpoczyna Ala, startując od liczby
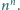 Kto ma strategię wygrywającą?
Kto ma strategię wygrywającą?
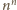 jest zielona; a więc (jak zwykle w tego typu zadaniach)
wygrywa dziewczyna.
jest zielona; a więc (jak zwykle w tego typu zadaniach)
wygrywa dziewczyna.
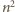 liczbami czerwonymi są wielokrotności
liczby
liczbami czerwonymi są wielokrotności
liczby
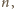 i tylko one; sprawdzenie własności (1), (2) jest natychmiastowe.
Sama liczba
i tylko one; sprawdzenie własności (1), (2) jest natychmiastowe.
Sama liczba
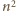 jest wszelako zielona (dzielenie przez
jest wszelako zielona (dzielenie przez
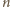 prowadzi do
czerwonej liczby
prowadzi do
czerwonej liczby
 ). Liczby z przedziału
). Liczby z przedziału
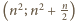 też są
zielone (dzielenie z zaokrągleniem prowadzi do
też są
zielone (dzielenie z zaokrągleniem prowadzi do
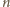 ). Zajmiemy się teraz
liczbami większymi.
). Zajmiemy się teraz
liczbami większymi.
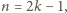 czyli
czyli
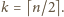 Weźmy pod uwagę
zbiór
Weźmy pod uwagę
zbiór
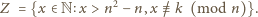
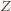 są zielone.
są zielone.
 będzie najmniejszą liczbą
czerwoną w zbiorze
będzie najmniejszą liczbą
czerwoną w zbiorze
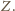 Wiemy już, że zielone są wszystkie liczby od
Wiemy już, że zielone są wszystkie liczby od
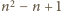 do
do
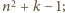 tak więc
tak więc
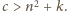 Niech
Niech
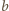 będzie największą liczbą spełniającą warunki
będzie największą liczbą spełniającą warunki
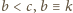 (mod
(mod
 ); zatem
); zatem
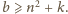 Jest ona osiągalna z liczby
Jest ona osiągalna z liczby
 ruchem
odejmowania.
ruchem
odejmowania.
 z zaokrągleniem, zastosowane do każdej z liczb
z zaokrągleniem, zastosowane do każdej z liczb
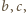 daje w wyniku tę samą liczbę
daje w wyniku tę samą liczbę
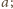 konkretnie: liczbę
konkretnie: liczbę
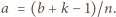 Liczba
Liczba
 jest czerwona, więc w myśl
własności (2) liczby
jest czerwona, więc w myśl
własności (2) liczby
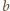 i
i
 (osiągalne z
(osiągalne z
 ) są zielone.
W myśl własności (1), istnieje ruch, prowadzący od liczby
) są zielone.
W myśl własności (1), istnieje ruch, prowadzący od liczby
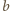 do jakiejś
liczby czerwonej. Nie jest to dzielenie z zaokrągleniem (które daje liczbę
do jakiejś
liczby czerwonej. Nie jest to dzielenie z zaokrągleniem (które daje liczbę
 ); zaś odejmowanie od
); zaś odejmowanie od
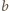 liczb
liczb
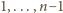 nie
wyprowadza ze zbioru
nie
wyprowadza ze zbioru
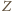 (skoro
(skoro
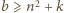 oraz
oraz
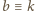 ).
Któraś z tak uzyskanych różnic powinna być liczbą czerwoną –
wbrew określeniu
).
Któraś z tak uzyskanych różnic powinna być liczbą czerwoną –
wbrew określeniu
 jako najmniejszej liczby czerwonej w zbiorze
jako najmniejszej liczby czerwonej w zbiorze
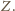
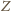 jest zielony.
Oczywiście
jest zielony.
Oczywiście
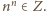 Ala wygrywa.
Ala wygrywa.
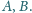 Rozważamy wszystkie
czworokąty wypukłe
Rozważamy wszystkie
czworokąty wypukłe
 położone w ustalonej półpłaszczyźnie
o krawędzi
położone w ustalonej półpłaszczyźnie
o krawędzi
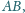 symetryczne względem prostej
symetryczne względem prostej
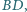 z kątem
prostym przy wierzchołku
z kątem
prostym przy wierzchołku
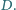 Wykazać, że istnieje punkt wspólny
wszystkich uzyskanych prostych
Wykazać, że istnieje punkt wspólny
wszystkich uzyskanych prostych
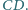
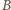 prowadzimy półprostą
prowadzimy półprostą
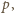 prostopadłą do
prostopadłą do
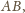 położoną w rozpatrywanej półpłaszczyźnie. Niech
położoną w rozpatrywanej półpłaszczyźnie. Niech
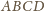 będzie jednym z rozważanych czworokątów. Trójkąt
będzie jednym z rozważanych czworokątów. Trójkąt
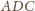 jest prostokątny, równoramienny. Stąd (i z wypukłości czworokąta
jest prostokątny, równoramienny. Stąd (i z wypukłości czworokąta
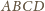 ) wynika, że punkt
) wynika, że punkt
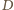 leży po tej stronie
leży po tej stronie
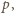 co
punkt
co
punkt
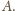 Półprosta
Półprosta
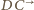 przecina więc
przecina więc
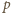 w pewnym
punkcie
w pewnym
punkcie
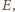 tworząc czworokąt wypukły
tworząc czworokąt wypukły
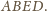 Ma on kąty proste
przy wierzchołkach
Ma on kąty proste
przy wierzchołkach
 i
i
 można na nim opisać okrąg.
Zatem
można na nim opisać okrąg.
Zatem
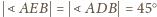 (ostatnia równość zachodzi,
bo
(ostatnia równość zachodzi,
bo
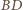 jest symetralną odcinka
jest symetralną odcinka
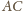 ). Stąd wniosek, że
). Stąd wniosek, że
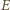 jest wierzchołkiem kwadratu, którego jednym bokiem jest odcinek
jest wierzchołkiem kwadratu, którego jednym bokiem jest odcinek
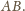 Jest to szukany punkt wspólny wszystkich możliwych prostych
Jest to szukany punkt wspólny wszystkich możliwych prostych
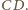
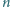 pytań (
pytań (
 ). Pewna liczba studentów
przystąpiła do tego egzaminu. Wiadomo, że dla każdych dwóch studentów
było przynajmniej jedno pytanie, na które obaj znali odpowiedź, ale dla
żadnej pary studentów nie było tak, że obaj znali odpowiedzi na dokładnie
te same pytania. Udowodnić, że do egzaminu przystąpiło co najwyżej
). Pewna liczba studentów
przystąpiła do tego egzaminu. Wiadomo, że dla każdych dwóch studentów
było przynajmniej jedno pytanie, na które obaj znali odpowiedź, ale dla
żadnej pary studentów nie było tak, że obaj znali odpowiedzi na dokładnie
te same pytania. Udowodnić, że do egzaminu przystąpiło co najwyżej
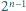 studentów.
studentów.
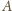 zbioru
zbioru
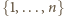 łączymy w nieuporządkowane pary
postaci
łączymy w nieuporządkowane pary
postaci
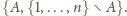 Takich par jest
Takich par jest
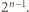 Wobec założenia
z treści zadania każdego studenta możemy utożsamiać jednoznacznie ze
zbiorem pytań, na które zna odpowiedź. Gdyby studentów było więcej niż
Wobec założenia
z treści zadania każdego studenta możemy utożsamiać jednoznacznie ze
zbiorem pytań, na które zna odpowiedź. Gdyby studentów było więcej niż
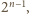 to znalazłoby się dwóch, którym odpowiadałyby zbiory
to znalazłoby się dwóch, którym odpowiadałyby zbiory
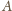 i
i
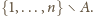 To jednak przeczyłoby założeniu, że na egzaminie było
pytanie, na które obaj znali odpowiedź.
To jednak przeczyłoby założeniu, że na egzaminie było
pytanie, na które obaj znali odpowiedź.
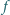 przekształcająca zbiór liczb
dodatnich w siebie, spełniająca dla wszystkich dodatnich
przekształcająca zbiór liczb
dodatnich w siebie, spełniająca dla wszystkich dodatnich
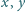 nierówność
nierówność
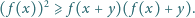
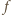 istnieje. Zauważmy, że
istnieje. Zauważmy, że
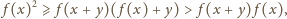
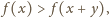 dla dowolnych
dla dowolnych
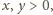 co oznacza, że
co oznacza, że
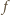 jest malejąca. Warunek z treści zadania można zapisać tak:
jest malejąca. Warunek z treści zadania można zapisać tak:
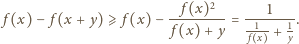
 i weźmy taką liczbę całkowitą
i weźmy taką liczbę całkowitą
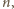 aby
aby
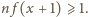 Wtedy dla
Wtedy dla
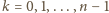 mamy
mamy
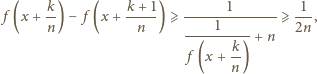
 nierówności, dostajemy
nierówności, dostajemy
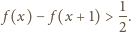
 zachodzi
nierówność
zachodzi
nierówność
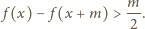
 tak duże, aby było
tak duże, aby było
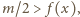 otrzymujemy
otrzymujemy
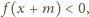 co przeczy temu, że
co przeczy temu, że
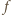 przyjmuje wyłącznie
wartości dodatnie.
przyjmuje wyłącznie
wartości dodatnie.
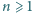 zachodzą następujące
równości:
zachodzą następujące
równości:
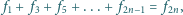
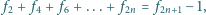
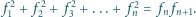
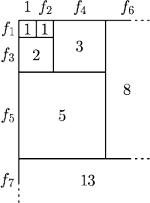
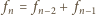 – następny kwadrat „pasuje” do
dwóch poprzednich.
– następny kwadrat „pasuje” do
dwóch poprzednich.
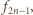 to cały prostokąt
ma taką właśnie szerokość, a wysokość równą następnemu
wyrazowi ciągu, czyli
to cały prostokąt
ma taką właśnie szerokość, a wysokość równą następnemu
wyrazowi ciągu, czyli
 Jednocześnie wysokość ta jest
równa
Jednocześnie wysokość ta jest
równa

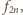 to prostokąt ma szerokość
równą
to prostokąt ma szerokość
równą
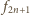 i zarazem równą
i zarazem równą
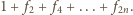
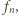 to
prostokąt
ma taką właśnie szerokość lub wysokość, a drugi z wymiarów
równy
to
prostokąt
ma taką właśnie szerokość lub wysokość, a drugi z wymiarów
równy
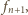 więc ma pole
więc ma pole
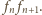 Jednocześnie pole to
jest równe
Jednocześnie pole to
jest równe
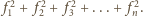
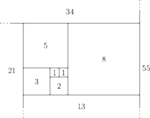
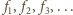 kolejno po prawej, na dole, po lewej,
na górze, znów po prawej itd., jak na
kolejno po prawej, na dole, po lewej,
na górze, znów po prawej itd., jak na  i szerokości 1, mając do dyspozycji duży zapas płyt o rozmiarach
i szerokości 1, mając do dyspozycji duży zapas płyt o rozmiarach
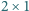 oraz
oraz
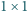 ?
?
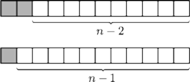
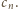 Dla
Dla
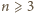 na początku
chodnika możemy położyć płytę
na początku
chodnika możemy położyć płytę
 a następnie na
a następnie na
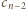 sposobów ułożyć resztę (chodnik o długości
sposobów ułożyć resztę (chodnik o długości
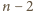 );
możemy też zacząć od płyty
);
możemy też zacząć od płyty
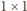 i wtedy na
i wtedy na
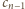 sposobów
ułożyć resztę. Stąd
sposobów
ułożyć resztę. Stąd
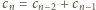 dla
dla
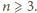 Otrzymany
wzór jest taki sam, jak dla ciągu Fibonacciego. Nietrudno sprawdzić, że
Otrzymany
wzór jest taki sam, jak dla ciągu Fibonacciego. Nietrudno sprawdzić, że
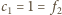 oraz
oraz
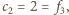 uzyskujemy więc wniosek, że
uzyskujemy więc wniosek, że
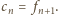

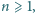
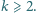
 takich jak opisano
w poprzednim zadaniu, można rozciąć na chodnik o długości
takich jak opisano
w poprzednim zadaniu, można rozciąć na chodnik o długości
 (od
lewej strony) oraz chodnik o długości
(od
lewej strony) oraz chodnik o długości
 (po prawej stronie) bez
rozcinania poszczególnych płyt (
(po prawej stronie) bez
rozcinania poszczególnych płyt (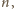 a po prawej chodnik długości
a po prawej chodnik długości
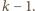 Z poprzedniego
zadania wiemy, że możliwości tych jest po lewej
Z poprzedniego
zadania wiemy, że możliwości tych jest po lewej
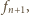 po prawej
po prawej
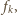 więc łącznie
więc łącznie
 Cięcie chodnika wymaga rozcinania płyty,
gdy w miejscu podziału leży płyta
Cięcie chodnika wymaga rozcinania płyty,
gdy w miejscu podziału leży płyta
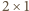 (
(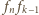 : układamy od lewej kolejno chodnik
długości
: układamy od lewej kolejno chodnik
długości
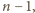 następnie płytę
następnie płytę
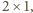 a po prawej chodnik
długości
a po prawej chodnik
długości
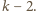 Wszystkich chodników, jak wiemy z poprzedniego
zadania, jest
Wszystkich chodników, jak wiemy z poprzedniego
zadania, jest
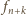 i każdy z nich da się rozciąć w opisany sposób
lub nie, stąd
i każdy z nich da się rozciąć w opisany sposób
lub nie, stąd
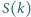 oznacza sumę cyfr liczby całkowitej
oznacza sumę cyfr liczby całkowitej
 w zapisie
dziesiętnym. Dowieść, że istnieje nieskończenie wiele takich dodatnich liczb
całkowitych
w zapisie
dziesiętnym. Dowieść, że istnieje nieskończenie wiele takich dodatnich liczb
całkowitych
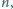 że
że

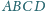 wierzchołek
wierzchołek
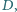 środek
sfery wpisanej oraz środek ciężkości czworościanu leżą na jednej prostej
wtedy i tylko wtedy, gdy pola trójkątów
środek
sfery wpisanej oraz środek ciężkości czworościanu leżą na jednej prostej
wtedy i tylko wtedy, gdy pola trójkątów
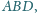
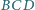 i
i
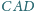 są równe.
są równe.
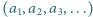 spełnia warunek
spełnia warunek
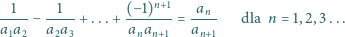
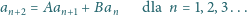
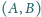 oraz wszystkie
pary wyrazów początkowych
oraz wszystkie
pary wyrazów początkowych
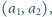 dla których ta rekurencja liniowa
generuje ciąg
dla których ta rekurencja liniowa
generuje ciąg
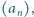 spełniający zadany na wstępie warunek.
spełniający zadany na wstępie warunek.
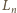 oznacza sumę po lewej stronie zależności, podanej
na początku zadania, zaś
oznacza sumę po lewej stronie zależności, podanej
na początku zadania, zaś
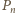 – ułamek po prawej stronie. Dla
– ułamek po prawej stronie. Dla
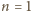 mamy
mamy
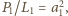 zatem równość
zatem równość
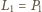 wymusza
wartość
wymusza
wartość
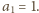 Dalej,
Dalej,
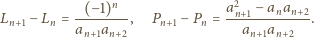
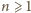 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
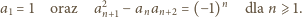
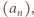 spełniający ten warunek, miałby również spełniać
rekurencję typu
spełniający ten warunek, miałby również spełniać
rekurencję typu
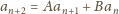
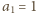 ), to dla
), to dla
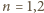 mielibyśmy
mielibyśmy

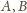 ) o wyznaczniku
) o wyznaczniku
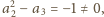 więc mający dokładnie
jedno rozwiązanie. Przy tym jest on spełniony dla
więc mający dokładnie
jedno rozwiązanie. Przy tym jest on spełniony dla
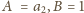 (co łatwo
stwierdzić, korzystając z drugiej pary równości). Stąd wniosek, że
jedynym kandydatem na postulowaną zależność rekurencyjną jest
równanie
(co łatwo
stwierdzić, korzystając z drugiej pary równości). Stąd wniosek, że
jedynym kandydatem na postulowaną zależność rekurencyjną jest
równanie
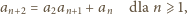
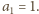 Wprowadźmy oznaczenia:
Wprowadźmy oznaczenia:
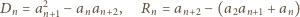
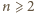 )
)
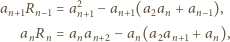
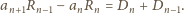
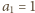 ) mamy:
) mamy:
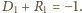
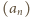 spełnia
wyjściową zależność, czyli warunki (1), to dla wszystkich
spełnia
wyjściową zależność, czyli warunki (1), to dla wszystkich
 mamy
mamy
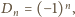 więc prawa strona (4) ma stale wartość 0; przy tym
więc prawa strona (4) ma stale wartość 0; przy tym
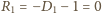 i ze wzoru (4) wynika, że
i ze wzoru (4) wynika, że
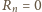 dla wszystkich
dla wszystkich
 – mamy zależność (3).
– mamy zależność (3).
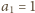 oraz
dowolnym
oraz
dowolnym
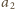 ) jest dla wszystkich
) jest dla wszystkich
 spełnione, czyli wszystkie
spełnione, czyli wszystkie
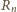 są zerami, to wobec (4):
są zerami, to wobec (4):
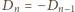 dla
dla
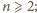 przy tym
przy tym
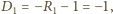 zatem
zatem
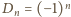 – a to jest zależność
(1).
– a to jest zależność
(1).
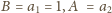 – dowolna liczba
naturalna.
– dowolna liczba
naturalna.