Teoria liczb Kącik początkującego olimpijczyka
Lemat o zwiększaniu wykładnika p-adycznego
O zależnościach między 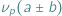 i
i 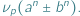
Teoria liczb Kącik początkującego olimpijczyka
O zależnościach między 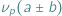 i
i 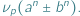
- Hop, hop, jest tam kto? - krzyczy 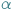 otoczona tłumem.
otoczona tłumem.
- Hop, hop, spójrz tutaj. - odpowiada 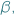 który co prawda słyszy
który co prawda słyszy 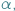 ale zupełnie jej nie widzi.
ale zupełnie jej nie widzi.
- Jakie "tutaj"? Przecież dookoła nie ma żywej duszy. - 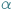 otoczona tłumem po raz kolejny usiłuje dostrzec
otoczona tłumem po raz kolejny usiłuje dostrzec 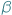 pośród otaczającej pustki.
pośród otaczającej pustki.

Rys. 1
Punkty z rysunku obok, jako środki kolejnych boków wielokąta, kodują pewien obrazek. Czy potrafisz go odtworzyć? Spróbuj!
Teoria liczb Kącik początkującego olimpijczyka
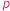 -adyczne
-adyczneO wygodnym narzędziu, przydatnym wszędzie tam, gdzie spotykamy rozkład na czynniki pierwsze
Każdej liczbie rzeczywistej możemy przypisać nieskończony ciąg cyfr jej rozwinięcia dziesiętnego. Jak wiadomo, jeżeli ciąg od pewnego miejsca się zapętla, to mamy do czynienia z liczbą wymierną. Inaczej rzecz ujmując, liczby wymierne mają okresowe rozwinięcie dziesiętne. Przyjmujemy tutaj, że tzw. rozwinięcie skończone jest rozwinięciem okresowym - od pewnego miejsca na każdej pozycji występuje wyłącznie cyfra 0.
Każdy, komu choć raz zdarzyło się grać na gitarze lub innym instrumencie strunowym, dobrze wie, że na wysokość dźwięku ma wpływ między innymi długość struny. Uderzając w struny zbudowane z tego samego materiału i o tych samych grubościach, lecz o różnych długościach, otrzymamy dwie różne częstotliwości drgań, a więc dwa dźwięki o różnych wysokościach. A jak to jest z instrumentami perkusyjnymi? Czy na podstawie brzmienia drgającej membrany bębenka można powiedzieć coś o jego kształcie?
Celem tego artykułu jest przybliżenie Czytelnikowi zagadnień i metod matematyki XVII wieku na przykładzie zadania trysekcji kąta i jego rozwiązania przez Kartezjusza. Przeplatają się tu metody geometryczne z algebraicznymi.
Gdy w parlamencie jedna partia ma większość, to ma całą władzę i może przegłosować praktycznie każdą ustawę. Co wydarzy się jednak, jeżeli ją straci, choćby jednym głosem? Jak wówczas wygląda rozkład sił w parlamencie? Czy dobrze odpowiada rozkładowi mandatów partii politycznych?
Za co Hillel Furstenberg (Uniwersytet Hebrajski w Jerozolimie) oraz Gregory Margulis (Uniwersytet Yale w New Haven) otrzymali tegoroczną nagrodę?
Planimetria Kącik początkującego olimpijczyka
O prostej Eulera i okręgu dziewięciu punktów.

wikipedia
Johannes Kepler (1571-1630)
Drugie prawo Keplera, mówiące o tym, że w równych odstępach czasu promień wodzący planety, poprowadzony od Słońca, zakreśla równe pola (patrz ilustracja na następnej stronie), było w dużym stopniu ignorowane w astronomii przednewtonowskiej. Na przykład w dziele Astronomia Carolina, z którego korzystał Newton, jest ono wyraźnie nieobecne. Wynikało to z jego niewielkiej przydatności do obliczeń położenia planet na ich orbitach.

John William Strutt
Lord Rayleigh, właściwie John William Strutt, 3. Baron Rayleigh (1842-1919) był laureatem Nagrody Nobla w dziedzinie fizyki w 1904 r. (badanie gęstości gazów i odkrycie, wspólnie z Sir W. Ramsayem, argonu). W 1877 roku w książce The Theory of Sound (vol. I, str. 123) opisał prawidłowość, którą można wyrazić następująco...
Wielomian jaki jest, każdy widzi. I każdy, kto widzi, wie również, że wielomiany miewają pierwiastki rzeczywiste (czyli miejsca zerowe), ale nie zawsze...
Wyobraźmy sobie, że wyborcy chcą wybrać parlament o rozmiarze 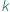 w małym kraju, w którym nie zaistniała jeszcze koncepcja partii politycznych (w związku z czym muszą głosować bezpośrednio na kandydatów, a nie na partie polityczne), albo że pracownicy pewnej firmy lub organizacji chcą wybrać
w małym kraju, w którym nie zaistniała jeszcze koncepcja partii politycznych (w związku z czym muszą głosować bezpośrednio na kandydatów, a nie na partie polityczne), albo że pracownicy pewnej firmy lub organizacji chcą wybrać 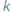 osób, które będą ich reprezentować w związkach zawodowych. Załóżmy, że każdy z wyborców głosuje, wskazując podzbiór kandydatów, których uważa za akceptowalnych: dla wyborcy
osób, które będą ich reprezentować w związkach zawodowych. Załóżmy, że każdy z wyborców głosuje, wskazując podzbiór kandydatów, których uważa za akceptowalnych: dla wyborcy 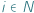 taki podzbiór akceptowalnych kandydatów będziemy oznaczać przez
taki podzbiór akceptowalnych kandydatów będziemy oznaczać przez 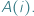 Pokażemy, że wskazanie "sprawiedliwego" sposobu przeprowadzenia takich wyborów jest nieoczywiste.
Pokażemy, że wskazanie "sprawiedliwego" sposobu przeprowadzenia takich wyborów jest nieoczywiste.
Planimetria Kącik początkującego olimpijczyka
Najbardziej królewskie części trójkąta i ich własności.

Andreas Scheits
Gottfried Wilhelm Leibniz
W marcu 1672 roku do Paryża przybył z misją dyplomatyczną od elektora mogunckiego młody prawnik, filozof i erudyta Gottfried Wilhelm Leibniz (1646-1716). Spotkanie z Christiaanem Huygensem (jesienią 1672 r.) przekonało Leibniza, że w matematyce jest nowicjuszem. Huygens, chcąc zbadać matematyczną przenikliwość Leibniza, rzucił mu takie oto wyzwanie: wyznaczyć sumę szeregu 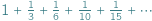 Leibniz zadanie wykonał (a Ty? rozwiązanie jest tutaj)...
Leibniz zadanie wykonał (a Ty? rozwiązanie jest tutaj)...
Zgodnie ze starożytnym żydowskim prawem, jeśli oskarżony w wyniku procesu przed Sanhedrynem został jednogłośnie uznany za winnego zarzucanych mu czynów, to odstępuje się od wymierzenia kary! Taka zasada dla wielu Czytelników jest zapewne szokująca. Jednak ówcześni twórcy prawa uznawali, że jednomyślność sędziów często wskazuje na niedopatrzenie przy ocenie dowodów winy. To mogło wypaczyć wynik procesu...
Piramidy w starożytnym Egipcie budowano na kształt ostrosłupa prawidłowego o podstawie kwadratu. Jak pokazują źródła historyczne, starożytni Egipcjanie potrafili obliczyć objętość takiego ostrosłupa. Jednak ich dobrze rozwinięta, jak na tamte czasy, matematyka, miała głównie zastosowanie praktyczne i raczej nikt nie formułował pytań, które miałyby na celu jedynie matematyczną rozrywkę. Jednym z matematyków, który szczególnie interesował się rozrywkowymi zastosowaniami królowej nauk, był Édouard Lucas, autor między innymi słynnej gry zwanej Wieżą Hanoi. W niniejszym artykule zwrócimy uwagę na sformułowany przez Lucasa problem z gatunku tych raczej mało praktycznych. Jak zobaczymy, ma on pewien związek z piramidami.
W stosunku do wielkości Ziemi wszystkie ziemskie nierówności (łańcuchy górskie, doliny) to znikome, zaniedbywalne zniekształcenia. Ponieważ w naszej skali nasze bliskie otoczenie przypomina płaską powierzchnię, więc nie powinno nas dziwić, że pierwsze geometryczne rozważania dotyczyły płaszczyzny.
W mieście Parzystkowo zacny burmistrz postanowił w nietypowy sposób zaktywizować społeczeństwo. Zarządził utworzenie stowarzyszeń, które wykonywać będą powierzone im zadania...