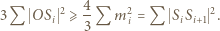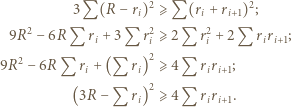Ciąg 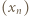 powstaje przez iterowanie funkcji
powstaje przez iterowanie funkcji 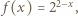 którą będziemy badać na przedziale
którą będziemy badać na przedziale ![[1,2].](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/3x-a051a26225a4472d5acd2ead6f6a678d0abff009-im-66,57,43-FF,FF,FF.gif) Ponieważ
Ponieważ 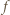 maleje od wartości
maleje od wartości 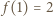 do wartości
do wartości 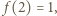 zatem odwzorowuje przedział
zatem odwzorowuje przedział ![[1,2]](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/7x-a051a26225a4472d5acd2ead6f6a678d0abff009-im-66,57,43-FF,FF,FF.gif) na siebie i ma w tym przedziale dokładnie jeden punkt stały
na siebie i ma w tym przedziale dokładnie jeden punkt stały 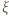 (tj. taki, że
(tj. taki, że 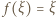 ). Obrazem przedziału
). Obrazem przedziału 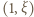 jest przedział
jest przedział 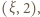 i na odwrót. Stąd wniosek, że wyrazy ciągu
i na odwrót. Stąd wniosek, że wyrazy ciągu 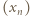 o numerach parzystych należą do jednego z tych przedziałów, a te o nieparzystych - do drugiego.
o numerach parzystych należą do jednego z tych przedziałów, a te o nieparzystych - do drugiego.
Równość 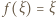 przepisujemy jako
przepisujemy jako 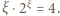 Funkcja
Funkcja 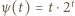 jest rosnąca; przy tym
jest rosnąca; przy tym
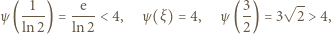
wobec czego
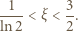 |
(1) |
Ponieważ (z założenia) 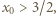 zatem
zatem 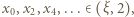 zaś
zaś 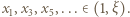
Użyjemy rachunku pochodnych. Oznaczmy (dla krótkości): 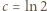 i zauważmy, że
i zauważmy, że 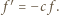 Niech
Niech 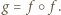 Wówczas
Wówczas
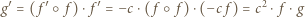
i dalej:
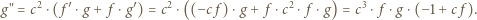 |
(2) |
Dla ![x ∈ [1,ξ]](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/1x-ebb224189cbd9ab5aa439f6248ce3382f71c3782-im-66,57,43-FF,FF,FF.gif) mamy nierówność
mamy nierówność 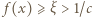 (por. (1)), więc wyrażenie w nawiasie po prawej stronie (2) ma w tych punktach wartość dodatnią. To znaczy, że funkcja
(por. (1)), więc wyrażenie w nawiasie po prawej stronie (2) ma w tych punktach wartość dodatnią. To znaczy, że funkcja 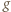 jest ściśle wypukła w przedziale
jest ściśle wypukła w przedziale ![|[1,ξ]](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/4x-ebb224189cbd9ab5aa439f6248ce3382f71c3782-im-66,57,43-FF,FF,FF.gif) ; a ponieważ
; a ponieważ 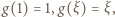 zatem
zatem
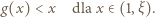 |
(3) |
Ciąg 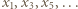 leży w przedziale
leży w przedziale 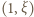 i jest generowany rekurencyjnie wzorem
i jest generowany rekurencyjnie wzorem 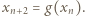 Nierówność (3) pokazuje, że jest to ciąg malejący, i w konsekwencji zbieżny. Jego granica musi być punktem stałym funkcji
Nierówność (3) pokazuje, że jest to ciąg malejący, i w konsekwencji zbieżny. Jego granica musi być punktem stałym funkcji 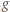 ; jednak nie ma takiego punktu w przedziale otwartym
; jednak nie ma takiego punktu w przedziale otwartym 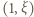 (nierówność (3)). W takim razie granicą tego ciągu musi być liczba 1.
(nierówność (3)). W takim razie granicą tego ciągu musi być liczba 1.
Funkcja ciągła 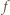 przeprowadza ten ciąg na ciąg rosnący
przeprowadza ten ciąg na ciąg rosnący 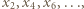 którego granicą jest wobec tego liczba
którego granicą jest wobec tego liczba 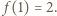 To dowodzi, że niezależnie od wyboru wyrazu początkowego
To dowodzi, że niezależnie od wyboru wyrazu początkowego 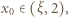 ciąg
ciąg 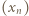 ma podciągi zbieżne do dwóch różnych granic: 1 oraz 2 (i do żadnej innej, bo dowolny podciąg ma nieskończenie wiele wspólnych wyrazów z jednym ze znalezionych podciągów, zbieżnych do 1 lub 2).
ma podciągi zbieżne do dwóch różnych granic: 1 oraz 2 (i do żadnej innej, bo dowolny podciąg ma nieskończenie wiele wspólnych wyrazów z jednym ze znalezionych podciągów, zbieżnych do 1 lub 2).
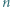 będzie dodatnią liczbą całkowitą. Wykazać, że
będzie dodatnią liczbą całkowitą. Wykazać, że 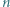 jest sumą dwóch elementów zbioru
jest sumą dwóch elementów zbioru 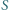 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy  jest iloczynem dwóch elementów zbioru
jest iloczynem dwóch elementów zbioru 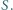
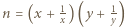 dla pewnych
dla pewnych 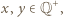 to
to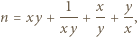
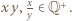 To dowodzi, że jeżeli
To dowodzi, że jeżeli 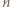 jest iloczynem dwóch elementów zbioru
jest iloczynem dwóch elementów zbioru 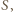 to jest również sumą dwóch elementów zbioru
to jest również sumą dwóch elementów zbioru 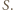
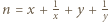 dla pewnych
dla pewnych 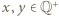 oraz niech
oraz niech 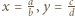 będą zapisami liczb
będą zapisami liczb 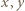 w postaci ułamków nieskracalnych, czyli
w postaci ułamków nieskracalnych, czyli 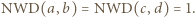 Wówczas
Wówczas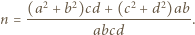
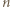 jest liczbą całkowitą, więc
jest liczbą całkowitą, więc 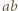 musi być dzielnikiem licznika powyższego ułamka. Stąd wniosek, że
musi być dzielnikiem licznika powyższego ułamka. Stąd wniosek, że 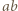 dzieli
dzieli 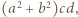 skąd wobec
skąd wobec 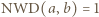 mamy, że
mamy, że 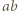 dzieli
dzieli 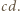 Analogicznie uzasadniamy, że
Analogicznie uzasadniamy, że 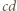 dzieli
dzieli 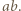 Zatem
Zatem 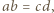 czyli
czyli 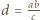 i w konsekwencji
i w konsekwencji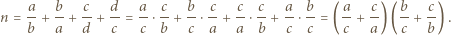
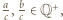 to
to 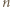 jest iloczynem dwóch elementów zbioru
jest iloczynem dwóch elementów zbioru 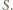
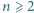 wyznaczyć taki wielomian
wyznaczyć taki wielomian 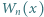 o współczynnikach wymiernych, że
o współczynnikach wymiernych, że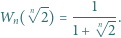
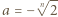 oraz
oraz 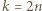 do tożsamości
do tożsamości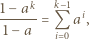
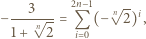
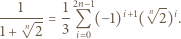
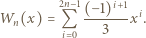
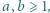 względnie pierwsze i takie, że wzór rekurencyjny
względnie pierwsze i takie, że wzór rekurencyjny
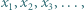 którego wszystkie wyrazy są liczbami złożonymi?
którego wszystkie wyrazy są liczbami złożonymi?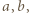 o jakie pyta zadanie, istnieją; można znaleźć wiele takich par. Przykład Autora (W. Bednarek):
o jakie pyta zadanie, istnieją; można znaleźć wiele takich par. Przykład Autora (W. Bednarek): 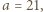
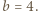 Wówczas
Wówczas 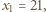
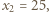 i dalej (dla każdego
i dalej (dla każdego 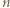 ):
):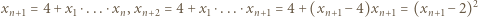
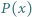 stopnia 2, o współczynnikach rzeczywistych, oraz liczba naturalna
stopnia 2, o współczynnikach rzeczywistych, oraz liczba naturalna 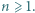 Udowodnić, że może istnieć co najwyżej jeden wielomian
Udowodnić, że może istnieć co najwyżej jeden wielomian 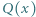 stopnia
stopnia 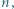 spełniający równanie
spełniający równanie 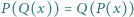 dla
dla 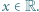
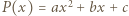
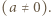 Przypuśćmy, że dla ustalonej liczby
Przypuśćmy, że dla ustalonej liczby 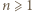 istnieją dwa różne wielomiany
istnieją dwa różne wielomiany 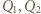 stopnia
stopnia 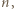 spełniające podane równanie. Oznaczmy ich współczynniki wiodące przez
spełniające podane równanie. Oznaczmy ich współczynniki wiodące przez 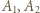 (więc
(więc 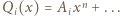 );
); 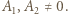 Przyrównując współczynniki wiodące po obu stronach równania
Przyrównując współczynniki wiodące po obu stronach równania 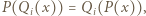 widzimy, że
widzimy, że 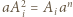 (dla
(dla 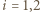 ). Zatem
). Zatem 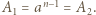 Stąd wynika, że różnica
Stąd wynika, że różnica 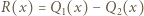 jest niezerowym wielomianem stopnia
jest niezerowym wielomianem stopnia 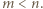
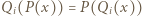 (dla
(dla 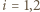 ) i przekształcamy uzyskaną równość:
) i przekształcamy uzyskaną równość: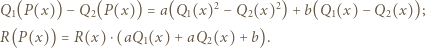
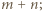 wielomian po lewej stronie ma stopień
wielomian po lewej stronie ma stopień 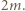 To już sprzeczność, skoro
To już sprzeczność, skoro 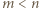 ; dwa różne wielomiany
; dwa różne wielomiany 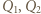 stopnia
stopnia 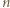 o podanej własności istnieć nie mogą.
o podanej własności istnieć nie mogą.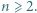
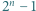 jest bezkwadratowa, to liczby
jest bezkwadratowa, to liczby 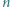 oraz
oraz 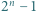 są względnie pierwsze.
są względnie pierwsze. oraz
oraz 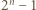 mają wspólny dzielnik pierwszy
mają wspólny dzielnik pierwszy 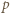 (jasne, że
(jasne, że 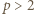 ). Wykażemy, że wówczas liczba
). Wykażemy, że wówczas liczba 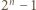 dzieli się przez
dzieli się przez 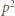 (nie jest więc bezkwadratowa). Zgodnie z małym twierdzeniem Fermata,
(nie jest więc bezkwadratowa). Zgodnie z małym twierdzeniem Fermata, 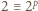 (mod
(mod 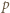 ). Podnosimy tę kongruencję stronami do potęgi
). Podnosimy tę kongruencję stronami do potęgi 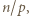 otrzymując
otrzymując 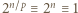 (mod
(mod 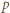 ). Zatem
). Zatem 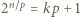 dla pewnej liczby całkowitej
dla pewnej liczby całkowitej 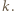 Stąd
Stąd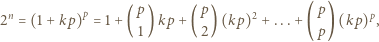
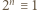 (mod
(mod 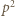 ); a to była nasza teza.
); a to była nasza teza.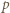 kontroluje dwie końcowe cyfry rozwinięcia (przy podstawie
kontroluje dwie końcowe cyfry rozwinięcia (przy podstawie 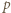 ) kolejnych potęg dwójki, pozwala znaleźć moment powtórzenia końcówki
) kolejnych potęg dwójki, pozwala znaleźć moment powtórzenia końcówki 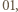 czyli wykładnik
czyli wykładnik 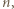 dla którego
dla którego 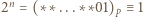 (mod
(mod 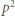 ). Powtarzamy tę procedurę dla kolejnych liczb pierwszych
). Powtarzamy tę procedurę dla kolejnych liczb pierwszych 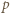 ; warto przy tym, dla oszczędności czasu, ograniczyć zakres wykładnika, np. do
; warto przy tym, dla oszczędności czasu, ograniczyć zakres wykładnika, np. do 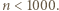 W ten sposób szybko znajdujemy parę
W ten sposób szybko znajdujemy parę 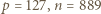 ; nie jest ona jednak szukanym kontrprzykładem, bowiem dla tej pary zachodzą związki
; nie jest ona jednak szukanym kontrprzykładem, bowiem dla tej pary zachodzą związki 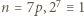 (mod
(mod 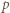 ), z których nietrudno wynika, że liczby
), z których nietrudno wynika, że liczby  i
i 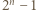 nie są względnie pierwsze.
nie są względnie pierwsze.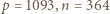 jest już dobra: gdyby liczby
jest już dobra: gdyby liczby 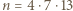 oraz
oraz  nie były względnie pierwsze, ta ostatnia musiałaby się dzielić przez 7 lub 13; ale minimalne wykładniki
nie były względnie pierwsze, ta ostatnia musiałaby się dzielić przez 7 lub 13; ale minimalne wykładniki 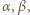 dla których
dla których 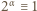 (mod 7),
(mod 7), 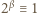 (mod 13), to
(mod 13), to 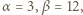 więc wykładnik
więc wykładnik 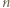 musiałby się dzielić przez 3; a tak nie jest. Skoro zaś ta para została wygenerowana przez algorytm, zapewniający podzielność
musiałby się dzielić przez 3; a tak nie jest. Skoro zaś ta para została wygenerowana przez algorytm, zapewniający podzielność 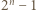 przez
przez 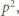 zatem liczba
zatem liczba 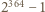 nie jest bezkwadratowa.
nie jest bezkwadratowa.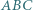 (nie prostokątny) jest wpisany w okrąg o średnicy
(nie prostokątny) jest wpisany w okrąg o średnicy 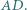 Punkt
Punkt 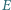 jest symetryczny do
jest symetryczny do 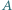 względem środka boku
względem środka boku 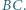 Dowieść, że okręgi opisane na trójkątach
Dowieść, że okręgi opisane na trójkątach 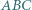 i
i  mają równe promienie.
mają równe promienie.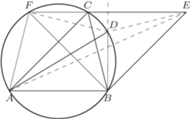
 jest równoległobokiem. Niech prosta
jest równoległobokiem. Niech prosta  przecina okrąg, opisany na trójkącie
przecina okrąg, opisany na trójkącie 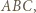 w punktach
w punktach 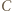 i
i 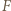 (gdy jest styczna, przyjmujemy
(gdy jest styczna, przyjmujemy 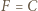 ). Powstaje trapez równoramienny
). Powstaje trapez równoramienny 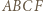 lub
lub 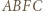 (gdy
(gdy 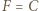 - trójkąt równoramienny). W każdym przypadku
- trójkąt równoramienny). W każdym przypadku 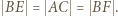
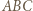 z założenia nie jest prostokątny, więc żaden jego bok nie pokrywa się ze średnicą
z założenia nie jest prostokątny, więc żaden jego bok nie pokrywa się ze średnicą 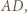 na której oparty jest kąt prosty
na której oparty jest kąt prosty 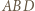 ; a ponieważ
; a ponieważ 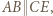 zatem
zatem 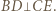 To znaczy, że w trójkącie równoramiennym
To znaczy, że w trójkącie równoramiennym 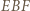 prosta
prosta 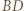 jest symetralną boku
jest symetralną boku 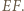 W konsekwencji trójkąt
W konsekwencji trójkąt 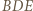 jest względem niej symetryczny do trójkąta
jest względem niej symetryczny do trójkąta 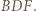 Okręgi opisane na tych trójkątach są przystające; to już teza, bo drugi z tych okręgów jest też opisany na trójkącie
Okręgi opisane na tych trójkątach są przystające; to już teza, bo drugi z tych okręgów jest też opisany na trójkącie 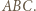
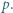 Funkcja
Funkcja 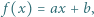 gdzie
gdzie 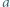 i
i 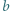 są liczbami całkowitymi, ma tę własność, że liczby
są liczbami całkowitymi, ma tę własność, że liczby
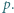 Wykazać, że
Wykazać, że 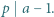
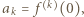 gdzie
gdzie 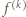 oznacza
oznacza 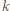 -krotne złożenie funkcji
-krotne złożenie funkcji 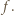 Z warunków zadania wynika, że dla pewnego
Z warunków zadania wynika, że dla pewnego 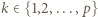 mamy
mamy 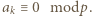 Jeżeli
Jeżeli 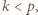 to
to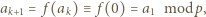
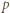 wyrazów ciągu
wyrazów ciągu 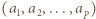 są parami różne. To oznacza, że
są parami różne. To oznacza, że 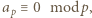 czyli
czyli 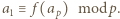
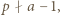 czyli
czyli 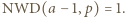 Wówczas istnieją takie liczby całkowite
Wówczas istnieją takie liczby całkowite 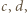 że
że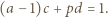
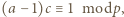 czyli
czyli 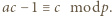 Z warunków zadania wynika, że dla pewnego
Z warunków zadania wynika, że dla pewnego 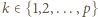 mamy
mamy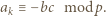
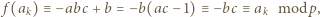
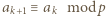 (gdzie w razie potrzeby przyjmujemy
(gdzie w razie potrzeby przyjmujemy 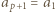 ). To stoi w sprzeczności z założeniem, że reszty z dzielenia przez
). To stoi w sprzeczności z założeniem, że reszty z dzielenia przez 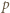 wyrazów ciągu
wyrazów ciągu 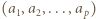 są parami różne.
są parami różne.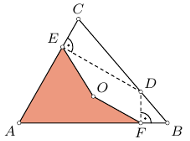
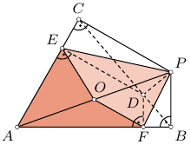
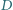 leży na boku
leży na boku 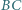 trójkąta ostrokątnego
trójkąta ostrokątnego 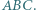 Punkty
Punkty 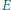 i
i 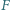 są rzutami prostokątnymi punktu
są rzutami prostokątnymi punktu 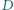 odpowiednio na boki
odpowiednio na boki 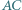 i
i 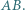 Punkt
Punkt 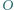 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie  Udowodnić, że pole czworokąta
Udowodnić, że pole czworokąta  jest równe połowie pola trójkąta
jest równe połowie pola trójkąta 
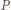 punkt symetryczny do
punkt symetryczny do 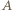 względem
względem 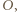 czyli taki punkt, że odcinek
czyli taki punkt, że odcinek 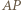 jest średnicą okręgu opisanego na trójkącie
jest średnicą okręgu opisanego na trójkącie 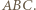 Wówczas
Wówczas 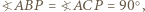 wobec czego
wobec czego 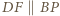 oraz
oraz 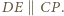 Stąd
Stąd ![F]=[PDF] |[BD](/math/temat/matematyka/geometria/planimetria/zadania/2018/03/25/zm-1562/9x-90debb24c13aa2006a155ff8aa83c0c64ef5c1cc-im-66,57,43-FF,FF,FF.gif) oraz
oraz ![[CDE]](/math/temat/matematyka/geometria/planimetria/zadania/2018/03/25/zm-1562/10x-90debb24c13aa2006a155ff8aa83c0c64ef5c1cc-im-66,57,43-FF,FF,FF.gif) a zatem
a zatem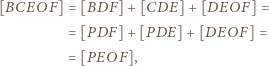
![[ℱ]](/math/temat/matematyka/geometria/planimetria/zadania/2018/03/25/zm-1562/12x-90debb24c13aa2006a155ff8aa83c0c64ef5c1cc-im-66,57,43-FF,FF,FF.gif) oznacza pole figury
oznacza pole figury 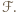 Ponieważ punkt
Ponieważ punkt 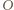 jest środkiem odcinka
jest środkiem odcinka 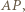 więc
więc ![F]=[AOF] [PO](/math/temat/matematyka/geometria/planimetria/zadania/2018/03/25/zm-1562/16x-90debb24c13aa2006a155ff8aa83c0c64ef5c1cc-im-66,57,43-FF,FF,FF.gif) oraz
oraz ![E]=[AOE] [PO](/math/temat/matematyka/geometria/planimetria/zadania/2018/03/25/zm-1562/17x-90debb24c13aa2006a155ff8aa83c0c64ef5c1cc-im-66,57,43-FF,FF,FF.gif) i w konsekwencji
i w konsekwencji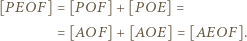
![EOF], |[BCEOF]](/math/temat/matematyka/geometria/planimetria/zadania/2018/03/25/zm-1562/19x-90debb24c13aa2006a155ff8aa83c0c64ef5c1cc-im-66,57,43-FF,FF,FF.gif) co jest równoznaczne z tezą zadania.
co jest równoznaczne z tezą zadania.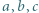 spełniają nierówność
spełniają nierówność 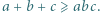 Udowodnić, że
Udowodnić, że 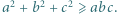
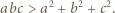
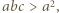 skąd
skąd 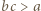 i analogicznie
i analogicznie 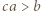 oraz
oraz 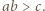 Ponadto mamy
Ponadto mamy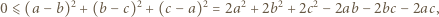
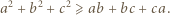
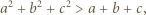
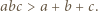
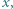 dla których każda z liczb
dla których każda z liczb 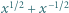 oraz
oraz 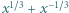 jest całkowita.
jest całkowita.
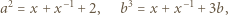
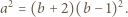
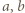 są naturalne, czynnik
są naturalne, czynnik 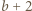 musi być kwadratem liczby naturalnej; więc
musi być kwadratem liczby naturalnej; więc 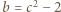
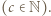 Zgodnie z (1), jest to suma liczb
Zgodnie z (1), jest to suma liczb 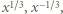 których iloczyn wynosi 1. Zatem
których iloczyn wynosi 1. Zatem 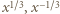 to pierwiastki trójmianu kwadratowego
to pierwiastki trójmianu kwadratowego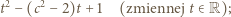
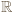 ) gdy
) gdy 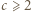 ; i są wówczas dodatnie. Wyznaczamy je zwykłą metodą, podnosimy do trzeciej potęgi, i dostajemy wniosek:
; i są wówczas dodatnie. Wyznaczamy je zwykłą metodą, podnosimy do trzeciej potęgi, i dostajemy wniosek: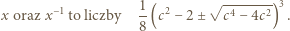
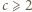 określamy wzorami (4) parę liczb rzeczywistych, wzajemnie odwrotnych:
określamy wzorami (4) parę liczb rzeczywistych, wzajemnie odwrotnych:  oraz
oraz 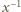 (jedna ze znakiem plus w nawiasie, druga ze znakiem minus). Wówczas
(jedna ze znakiem plus w nawiasie, druga ze znakiem minus). Wówczas 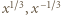 są pierwiastkami trójmianu (3); ich suma wynosi
są pierwiastkami trójmianu (3); ich suma wynosi 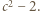 Liczby
Liczby 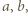 zdefiniowane wzorami (1), spełniają równość (2); a ponieważ
zdefiniowane wzorami (1), spełniają równość (2); a ponieważ 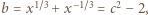 zatem prawa strona wzoru (2) jest kwadratem liczby całkowitej, więc liczba
zatem prawa strona wzoru (2) jest kwadratem liczby całkowitej, więc liczba 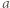 jest całkowita (liczba
jest całkowita (liczba 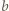 oczywiście też).
oczywiście też).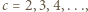 przedstawia ogólną postać liczb
przedstawia ogólną postać liczb 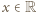 o rozważanej w zadaniu własności.
o rozważanej w zadaniu własności.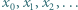 jest określony wzorem rekurencyjnym
jest określony wzorem rekurencyjnym 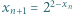 dla
dla 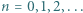 ; wyraz początkowy
; wyraz początkowy 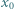 jest dowolną liczbą z przedziału
jest dowolną liczbą z przedziału 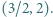 Wyznaczyć wszystkie liczby, będące granicami zbieżnych podciągów ciągu
Wyznaczyć wszystkie liczby, będące granicami zbieżnych podciągów ciągu 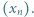
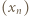 powstaje przez iterowanie funkcji
powstaje przez iterowanie funkcji 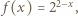 którą będziemy badać na przedziale
którą będziemy badać na przedziale ![[1,2].](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/3x-a051a26225a4472d5acd2ead6f6a678d0abff009-im-66,57,43-FF,FF,FF.gif) Ponieważ
Ponieważ 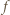 maleje od wartości
maleje od wartości 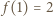 do wartości
do wartości 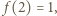 zatem odwzorowuje przedział
zatem odwzorowuje przedział ![[1,2]](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/7x-a051a26225a4472d5acd2ead6f6a678d0abff009-im-66,57,43-FF,FF,FF.gif) na siebie i ma w tym przedziale dokładnie jeden punkt stały
na siebie i ma w tym przedziale dokładnie jeden punkt stały 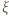 (tj. taki, że
(tj. taki, że 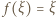 ). Obrazem przedziału
). Obrazem przedziału 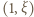 jest przedział
jest przedział 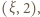 i na odwrót. Stąd wniosek, że wyrazy ciągu
i na odwrót. Stąd wniosek, że wyrazy ciągu 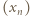 o numerach parzystych należą do jednego z tych przedziałów, a te o nieparzystych - do drugiego.
o numerach parzystych należą do jednego z tych przedziałów, a te o nieparzystych - do drugiego.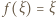 przepisujemy jako
przepisujemy jako 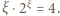 Funkcja
Funkcja 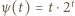 jest rosnąca; przy tym
jest rosnąca; przy tym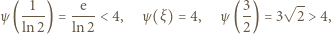
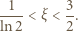
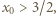 zatem
zatem 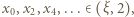 zaś
zaś 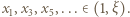
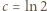 i zauważmy, że
i zauważmy, że 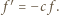 Niech
Niech 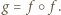 Wówczas
Wówczas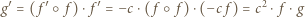
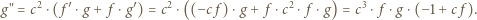
![x ∈ [1,ξ]](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/1x-ebb224189cbd9ab5aa439f6248ce3382f71c3782-im-66,57,43-FF,FF,FF.gif) mamy nierówność
mamy nierówność 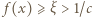 (por. (1)), więc wyrażenie w nawiasie po prawej stronie (2) ma w tych punktach wartość dodatnią. To znaczy, że funkcja
(por. (1)), więc wyrażenie w nawiasie po prawej stronie (2) ma w tych punktach wartość dodatnią. To znaczy, że funkcja 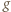 jest ściśle wypukła w przedziale
jest ściśle wypukła w przedziale ![|[1,ξ]](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/4x-ebb224189cbd9ab5aa439f6248ce3382f71c3782-im-66,57,43-FF,FF,FF.gif) ; a ponieważ
; a ponieważ 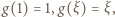 zatem
zatem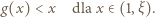
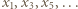 leży w przedziale
leży w przedziale 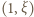 i jest generowany rekurencyjnie wzorem
i jest generowany rekurencyjnie wzorem 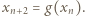 Nierówność (3) pokazuje, że jest to ciąg malejący, i w konsekwencji zbieżny. Jego granica musi być punktem stałym funkcji
Nierówność (3) pokazuje, że jest to ciąg malejący, i w konsekwencji zbieżny. Jego granica musi być punktem stałym funkcji 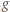 ; jednak nie ma takiego punktu w przedziale otwartym
; jednak nie ma takiego punktu w przedziale otwartym 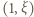 (nierówność (3)). W takim razie granicą tego ciągu musi być liczba 1.
(nierówność (3)). W takim razie granicą tego ciągu musi być liczba 1.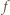 przeprowadza ten ciąg na ciąg rosnący
przeprowadza ten ciąg na ciąg rosnący 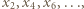 którego granicą jest wobec tego liczba
którego granicą jest wobec tego liczba 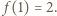 To dowodzi, że niezależnie od wyboru wyrazu początkowego
To dowodzi, że niezależnie od wyboru wyrazu początkowego 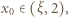 ciąg
ciąg 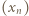 ma podciągi zbieżne do dwóch różnych granic: 1 oraz 2 (i do żadnej innej, bo dowolny podciąg ma nieskończenie wiele wspólnych wyrazów z jednym ze znalezionych podciągów, zbieżnych do 1 lub 2).
ma podciągi zbieżne do dwóch różnych granic: 1 oraz 2 (i do żadnej innej, bo dowolny podciąg ma nieskończenie wiele wspólnych wyrazów z jednym ze znalezionych podciągów, zbieżnych do 1 lub 2).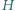 jest ortocentrum trójkąta
jest ortocentrum trójkąta 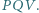
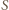 zamienia punkty
zamienia punkty 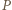 i
i 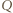 oraz punkty
oraz punkty 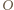 i
i 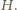 Symetralna odcinka
Symetralna odcinka 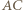 jest do niego prostopadła, przechodzi przez jego środek
jest do niego prostopadła, przechodzi przez jego środek 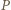 i przez
i przez 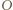 - środek okręgu, w którym
- środek okręgu, w którym 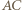 jest cięciwą. Jej obrazem w symetrii względem
jest cięciwą. Jej obrazem w symetrii względem 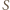 jest więc prosta prostopadła do
jest więc prosta prostopadła do 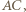 przechodząca przez
przechodząca przez 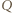 (czyli wysokość trójkąta
(czyli wysokość trójkąta 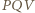 ) i przez
) i przez 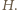 Analogicznie wysokość trójkąta
Analogicznie wysokość trójkąta 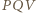 z wierzchołka
z wierzchołka 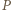 też przechodzi przez
też przechodzi przez 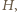 co kończy dowód.
co kończy dowód.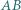 i
i 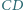 przecinają się w punkcie
przecinają się w punkcie 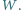 Wykaż, że
Wykaż, że 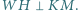
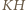 i
i 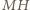 są wysokościami trójkąta
są wysokościami trójkąta 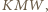 więc
więc 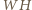 też jest.
też jest.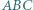 jest styczny do boków
jest styczny do boków 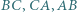 odpowiednio w punktach
odpowiednio w punktach 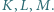 Udowodnij, że proste przechodzące przez środki odcinków
Udowodnij, że proste przechodzące przez środki odcinków 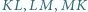 i prostopadłe odpowiednio do boków
i prostopadłe odpowiednio do boków 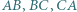 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.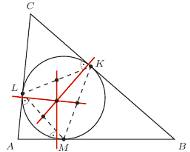
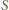 oznacza środek ciężkości trójkąta
oznacza środek ciężkości trójkąta 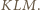 Wówczas jednokładność o środku
Wówczas jednokładność o środku 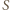 i skali -2 przeprowadza środek odcinka
i skali -2 przeprowadza środek odcinka 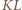 na punkt
na punkt 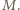 Wobec tego przy tej jednokładności obrazem prostej przechodzącej przez tenże środek i prostopadłej do
Wobec tego przy tej jednokładności obrazem prostej przechodzącej przez tenże środek i prostopadłej do 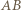 jest prosta przechodząca przez punkt
jest prosta przechodząca przez punkt 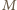 i prostopadła do
i prostopadła do 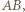 czyli prosta przechodząca przez środek
czyli prosta przechodząca przez środek 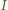 okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt 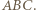 Analogicznie obrazami pozostałych opisanych w zadaniu prostych też są proste przez
Analogicznie obrazami pozostałych opisanych w zadaniu prostych też są proste przez 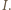 Stąd również wyjściowe proste są współpękowe.
Stąd również wyjściowe proste są współpękowe.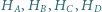 będą odpowiednio ortocentrami trójkątów
będą odpowiednio ortocentrami trójkątów 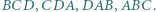 Wykaż, że odcinki
Wykaż, że odcinki 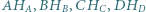 mają wspólny punkt.
mają wspólny punkt. jest ich wspólnym środkiem.
jest ich wspólnym środkiem. oraz
oraz 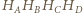 są przystające, co daje inne rozwiązanie zadania 4 z
są przystające, co daje inne rozwiązanie zadania 4 z 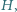 środek ciężkości
środek ciężkości 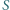 i środek okręgu opisanego
i środek okręgu opisanego 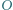 leżą na jednej prostej (prostej Eulera), w tej kolejności i
leżą na jednej prostej (prostej Eulera), w tej kolejności i 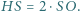
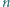 -kąta foremnego wpisanego w okrąg o promieniu 1.
-kąta foremnego wpisanego w okrąg o promieniu 1.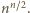
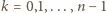 oraz
oraz 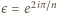 niech
niech 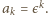 Wówczas liczby
Wówczas liczby 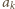 wyznaczają na płaszczyźnie zespolonej
wyznaczają na płaszczyźnie zespolonej  -kąt foremny wpisany w okrąg o promieniu
-kąt foremny wpisany w okrąg o promieniu 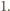
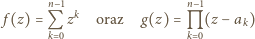
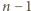 mają równe współczynniki przy najwyższej potędze
mają równe współczynniki przy najwyższej potędze  oraz
oraz 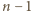 wspólnych pierwiastków zespolonych, mianowicie
wspólnych pierwiastków zespolonych, mianowicie 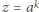 dla
dla 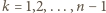 (ze względu na równość
(ze względu na równość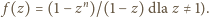
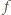 i
i 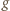 są równe, w szczególności
są równe, w szczególności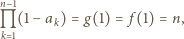
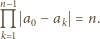
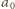 rozważanego wielokąta (czyli, z uwagi na symetrię, dowolny ustalony wierzchołek) jest równa
rozważanego wielokąta (czyli, z uwagi na symetrię, dowolny ustalony wierzchołek) jest równa 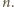 Wobec tego
Wobec tego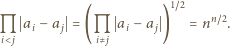
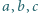 o tej własności, że każdy z trójmianów kwadratowych
o tej własności, że każdy z trójmianów kwadratowych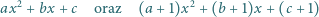
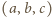 ma opisaną własność. Wówczas trójka
ma opisaną własność. Wówczas trójka 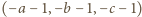 również ją ma, więc możemy bez straty ogólności założyć, że
również ją ma, więc możemy bez straty ogólności założyć, że 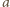 jest liczbą parzystą.
jest liczbą parzystą.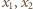 są całkowitymi pierwiastkami trójmianu
są całkowitymi pierwiastkami trójmianu 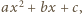 to liczby
to liczby 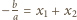 oraz
oraz 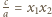 są całkowite, co wobec parzystości
są całkowite, co wobec parzystości  oznacza, że liczby
oznacza, że liczby 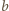 oraz
oraz  również są parzyste.
również są parzyste.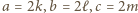 dla całkowitych
dla całkowitych 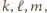 to wyróżnik trójmianu
to wyróżnik trójmianu 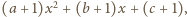 równy
równy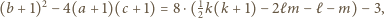
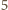 przy dzieleniu przez
przy dzieleniu przez 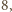 co oznacza, że nie może być kwadratem liczby całkowitej. Uzyskana sprzeczność kończy dowód.
co oznacza, że nie może być kwadratem liczby całkowitej. Uzyskana sprzeczność kończy dowód.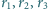 są parami styczne zewnętrznie oraz są styczne wewnętrznie do okręgu o promieniu
są parami styczne zewnętrznie oraz są styczne wewnętrznie do okręgu o promieniu 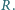 Wykazać, że
Wykazać, że
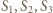 środki tych trzech okręgów, a środek dużego okręgu przez
środki tych trzech okręgów, a środek dużego okręgu przez 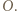 Zgodnie z warunkami zadania,
Zgodnie z warunkami zadania,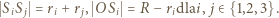
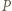 będzie środkiem ciężkości trójkąta
będzie środkiem ciężkości trójkąta 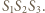 Jest to punkt minimalizujący sumę kwadratów odległości od wierzchołków (znany fakt, zresztą łatwy do wykazania). Zatem
Jest to punkt minimalizujący sumę kwadratów odległości od wierzchołków (znany fakt, zresztą łatwy do wykazania). Zatem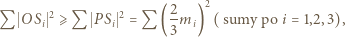
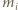 jest długością środkowej, wychodzącej z wierzchołka
jest długością środkowej, wychodzącej z wierzchołka 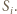 Suma kwadratów długości środkowych to
Suma kwadratów długości środkowych to 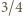 sumy kwadratów długości boków (kolejny znany wzór). Nierówność (2) pokazuje więc, że
sumy kwadratów długości boków (kolejny znany wzór). Nierówność (2) pokazuje więc, że