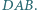Gdy 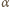 przebiega przedział
przebiega przedział 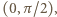 wartość
wartość 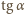 przebiega zbiór wszystkich liczb dodatnich. Należy więc znaleźć kres górny funkcji
przebiega zbiór wszystkich liczb dodatnich. Należy więc znaleźć kres górny funkcji 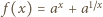 zmiennej
zmiennej 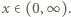 Ponieważ
Ponieważ 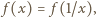 kres górny na przedziale
kres górny na przedziale 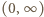 jest taki sam, jak na przedziale
jest taki sam, jak na przedziale 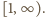 Pochodna funkcji
Pochodna funkcji 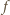 ma po prostym przekształceniu postać
ma po prostym przekształceniu postać
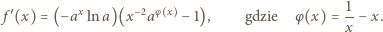
Skoro 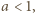 czynnik w pierwszym nawiasie jest stale dodatni. Czynnik w drugim nawiasie ma taki sam znak jak wyrażenie
czynnik w pierwszym nawiasie jest stale dodatni. Czynnik w drugim nawiasie ma taki sam znak jak wyrażenie
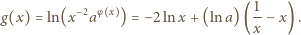
Teraz badamy funkcję 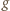 w przedziale
w przedziale 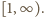 Jej pochodna:
Jej pochodna:
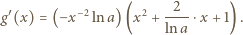
I znów, czynnik w pierwszym nawiasie jest dodatni. W drugim nawiasie widzimy trójmian kwadratowy, którego pierwiastki (rzeczywiste lub nie) mają iloczyn równy 1; w przedziale 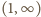 może być co najwyżej jeden pierwiastek. Dla dużych
może być co najwyżej jeden pierwiastek. Dla dużych 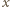 trójmian ma wartości dodatnie. Zatem wartości
trójmian ma wartości dodatnie. Zatem wartości 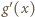 albo są dodatnie w całym przedziale
albo są dodatnie w całym przedziale 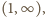 albo są - przedziałami - najpierw ujemne, potem dodatnie. Funkcja
albo są - przedziałami - najpierw ujemne, potem dodatnie. Funkcja 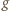 jest więc albo rosnąca, albo (kolejno) malejąca-rosnąca. A ponieważ
jest więc albo rosnąca, albo (kolejno) malejąca-rosnąca. A ponieważ 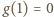 oraz
oraz 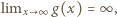 wynika stąd, że także wartości
wynika stąd, że także wartości 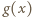 są albo stale dodatnie, albo (przedziałami, od lewej) ujemne-dodatnie.
są albo stale dodatnie, albo (przedziałami, od lewej) ujemne-dodatnie.
Funkcja 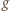 ma taki znak, jak
ma taki znak, jak 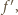 wobec czego możemy powtórzyć rozumowanie: funkcja
wobec czego możemy powtórzyć rozumowanie: funkcja 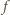 jest albo rosnąca, albo (kolejno) malejąca-rosnąca. W każdym przypadku jej kresem górnym na przedziale
jest albo rosnąca, albo (kolejno) malejąca-rosnąca. W każdym przypadku jej kresem górnym na przedziale 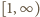 jest jej wartość lub granica w jednym z końców przedziału. Otrzymujemy wynik:
jest jej wartość lub granica w jednym z końców przedziału. Otrzymujemy wynik:
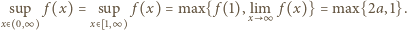
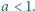 Obliczyć kres górny zbioru wartości wyrażenia
Obliczyć kres górny zbioru wartości wyrażenia 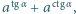 gdy zmienna
gdy zmienna 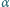 przebiega przedział
przebiega przedział 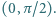
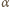 przebiega przedział
przebiega przedział 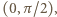 wartość
wartość 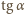 przebiega zbiór wszystkich liczb dodatnich. Należy więc znaleźć kres górny funkcji
przebiega zbiór wszystkich liczb dodatnich. Należy więc znaleźć kres górny funkcji 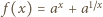 zmiennej
zmiennej 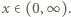 Ponieważ
Ponieważ 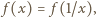 kres górny na przedziale
kres górny na przedziale 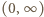 jest taki sam, jak na przedziale
jest taki sam, jak na przedziale 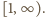 Pochodna funkcji
Pochodna funkcji 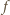 ma po prostym przekształceniu postać
ma po prostym przekształceniu postać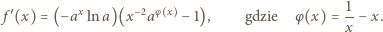
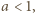 czynnik w pierwszym nawiasie jest stale dodatni. Czynnik w drugim nawiasie ma taki sam znak jak wyrażenie
czynnik w pierwszym nawiasie jest stale dodatni. Czynnik w drugim nawiasie ma taki sam znak jak wyrażenie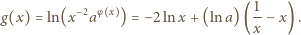
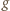 w przedziale
w przedziale 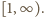 Jej pochodna:
Jej pochodna: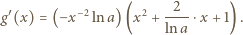
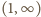 może być co najwyżej jeden pierwiastek. Dla dużych
może być co najwyżej jeden pierwiastek. Dla dużych 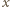 trójmian ma wartości dodatnie. Zatem wartości
trójmian ma wartości dodatnie. Zatem wartości 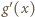 albo są dodatnie w całym przedziale
albo są dodatnie w całym przedziale 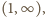 albo są - przedziałami - najpierw ujemne, potem dodatnie. Funkcja
albo są - przedziałami - najpierw ujemne, potem dodatnie. Funkcja 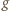 jest więc albo rosnąca, albo (kolejno) malejąca-rosnąca. A ponieważ
jest więc albo rosnąca, albo (kolejno) malejąca-rosnąca. A ponieważ 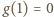 oraz
oraz 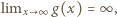 wynika stąd, że także wartości
wynika stąd, że także wartości 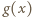 są albo stale dodatnie, albo (przedziałami, od lewej) ujemne-dodatnie.
są albo stale dodatnie, albo (przedziałami, od lewej) ujemne-dodatnie.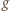 ma taki znak, jak
ma taki znak, jak 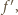 wobec czego możemy powtórzyć rozumowanie: funkcja
wobec czego możemy powtórzyć rozumowanie: funkcja 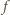 jest albo rosnąca, albo (kolejno) malejąca-rosnąca. W każdym przypadku jej kresem górnym na przedziale
jest albo rosnąca, albo (kolejno) malejąca-rosnąca. W każdym przypadku jej kresem górnym na przedziale 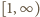 jest jej wartość lub granica w jednym z końców przedziału. Otrzymujemy wynik:
jest jej wartość lub granica w jednym z końców przedziału. Otrzymujemy wynik: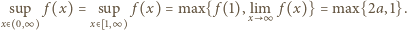
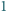 pomalowano na pewien kolor w taki sposób, że jeżeli dla pewnych dwóch liczb
pomalowano na pewien kolor w taki sposób, że jeżeli dla pewnych dwóch liczb 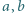 większych od
większych od 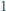 liczba
liczba 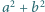 jest podzielna przez
jest podzielna przez 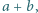 to
to 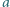 ma ten sam kolor, co
ma ten sam kolor, co 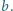 Jaka jest największa możliwa liczba kolorów użytych do pomalowania liczb?
Jaka jest największa możliwa liczba kolorów użytych do pomalowania liczb?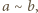 jeżeli
jeżeli 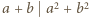 oraz niech
oraz niech 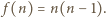 Zauważmy, że dla każdego
Zauważmy, że dla każdego 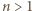 liczba
liczba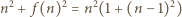
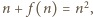 a zatem
a zatem 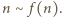 Ponadto, dla każdego
Ponadto, dla każdego 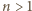 liczba
liczba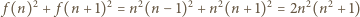
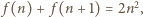 skąd wniosek, że
skąd wniosek, że 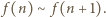 Wobec tego dla dowolnych liczb całkowitych
Wobec tego dla dowolnych liczb całkowitych 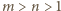 otrzymujemy
otrzymujemy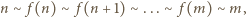
 i
i 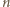 pomalowano tym samym kolorem.
pomalowano tym samym kolorem.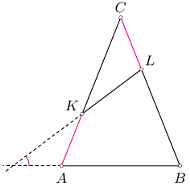
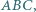 w którym
w którym 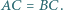 Na odcinkach
Na odcinkach 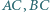 znajdują się odpowiednio takie punkty
znajdują się odpowiednio takie punkty 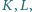 że
że 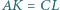 oraz
oraz 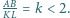 Wyznaczyć, w zależności od
Wyznaczyć, w zależności od 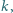 miarę kąta między prostymi
miarę kąta między prostymi 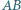 i
i 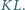
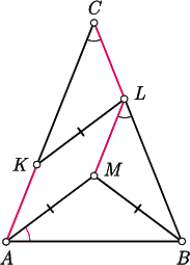
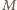 będzie takim punktem, że czworokąt
będzie takim punktem, że czworokąt 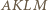 jest równoległobokiem. Wówczas
jest równoległobokiem. Wówczas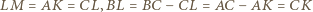
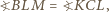
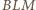 oraz
oraz 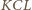 są przystające (cecha bok-kąt-bok). Zatem
są przystające (cecha bok-kąt-bok). Zatem 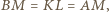 czyli trójkąt
czyli trójkąt 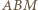 jest równoramienny, więc
jest równoramienny, więc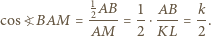
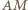 i
i 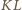 są równoległe, więc
są równoległe, więc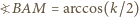
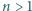 oraz dla dowolnych liczb rzeczywistych dodatnich
oraz dla dowolnych liczb rzeczywistych dodatnich 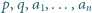 zachodzi nierówność
zachodzi nierówność
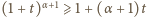 (słusznej dla
(słusznej dla 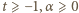 ) wykonujemy "przesunięcie zmiennej"
) wykonujemy "przesunięcie zmiennej" 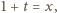 uzyskując postać
uzyskując postać
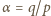 oraz
oraz 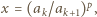 dostajemy
dostajemy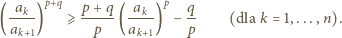
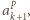 otrzymując
otrzymując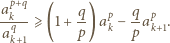
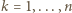 ) to teza zadania.
) to teza zadania.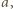 zaś dwie przyległe do niej ściany mają krawędzie długości
zaś dwie przyległe do niej ściany mają krawędzie długości 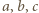 oraz
oraz 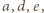 przy czym krawędzie
przy czym krawędzie 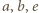 mają wspólny koniec oraz krawędzie
mają wspólny koniec oraz krawędzie 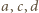 mają wspólny koniec. Wówczas
mają wspólny koniec. Wówczas 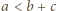 oraz
oraz 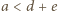 ; stąd
; stąd 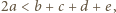 wobec czego musi zachodzić co najmniej jedna z nierówności
wobec czego musi zachodzić co najmniej jedna z nierówności 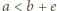 lub
lub 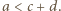 Zatem co najmniej jeden z końców krawędzi
Zatem co najmniej jeden z końców krawędzi  nie jest wierzchołkiem ciekawym.
nie jest wierzchołkiem ciekawym.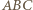 - trójkąt prostokątny;
- trójkąt prostokątny; 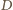 - środek przeciwprostokątnej
- środek przeciwprostokątnej 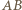 ;
; 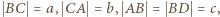 przy czym
przy czym 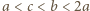 (np.
(np. 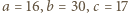 ). Z punktu
). Z punktu 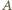 wychodzą krawędzie długości
wychodzą krawędzie długości 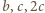 ; z punktu
; z punktu 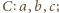 z punktu
z punktu 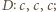 każda z tych trójek spełnia warunek trójkąta. Pozostaje wierzchołek
każda z tych trójek spełnia warunek trójkąta. Pozostaje wierzchołek 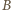 - jedyny ciekawy (wspólny koniec krawędzi
- jedyny ciekawy (wspólny koniec krawędzi 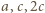 ). Teraz wystarczy wyjść w przestrzeń i nieznacznie przemieścić wierzchołek
). Teraz wystarczy wyjść w przestrzeń i nieznacznie przemieścić wierzchołek 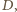 usuwając go prostopadle z płaszczyzny
usuwając go prostopadle z płaszczyzny 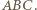 Wychodzące zeń krawędzie trochę się wydłużą. Przy małym przemieszczeniu rozważane nierówności (ostre) pozostaną w mocy; punkt
Wychodzące zeń krawędzie trochę się wydłużą. Przy małym przemieszczeniu rozważane nierówności (ostre) pozostaną w mocy; punkt 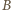 nadal będzie jedynym wierzchołkiem ciekawym.
nadal będzie jedynym wierzchołkiem ciekawym.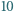 liczby naturalnej
liczby naturalnej 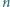 istnieje taka liczba naturalna
istnieje taka liczba naturalna 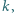 że pierwsza i ostatnia cyfra liczby
że pierwsza i ostatnia cyfra liczby 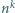 są równe.
są równe.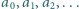 jest określony wzorem rekurencyjnym:
jest określony wzorem rekurencyjnym: 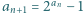 ; wyraz początkowy
; wyraz początkowy 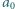 jest liczbą pierwszą. Dowieść, że dla każdego
jest liczbą pierwszą. Dowieść, że dla każdego 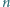 różnica
różnica 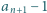 jest podzielna przez
jest podzielna przez 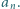
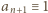 (mod
(mod 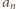 ) - po wprowadzeniu określenia liczby
) - po wprowadzeniu określenia liczby 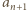 i dodaniu stronami jedynki - ma postać
i dodaniu stronami jedynki - ma postać
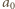 jest pierwsza, więc
jest pierwsza, więc 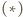 zachodzi dla
zachodzi dla 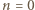 (małe twierdzenie Fermata). Dalej indukcja: przyjmijmy słuszność
(małe twierdzenie Fermata). Dalej indukcja: przyjmijmy słuszność 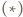 dla pewnego
dla pewnego 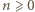 ; istnieje zatem liczba
; istnieje zatem liczba 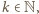 dla której
dla której 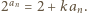 Odejmujemy stronami jedynkę i mamy
Odejmujemy stronami jedynkę i mamy 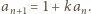 Z określenia
Z określenia 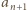 wynika ponadto, że
wynika ponadto, że 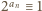 (mod
(mod 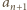 ). Tak więc
). Tak więc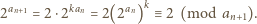
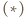 z
z 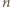 zastąpionym przez
zastąpionym przez 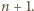 To kończy dowód indukcyjny.
To kończy dowód indukcyjny.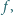 określone na zbiorze wszystkich liczb rzeczywistych różnych od zera, przyjmujące wartości w tym samym zbiorze, i spełniające równanie funkcyjne
określone na zbiorze wszystkich liczb rzeczywistych różnych od zera, przyjmujące wartości w tym samym zbiorze, i spełniające równanie funkcyjne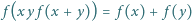
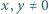 takiej, że
takiej, że 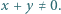
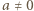 i przyjmijmy
i przyjmijmy 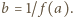 Załóżmy, że
Załóżmy, że 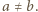 Możemy wówczas podstawić w podanym równaniu
Możemy wówczas podstawić w podanym równaniu 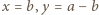 (bo
(bo 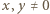 ), otrzymując związek
), otrzymując związek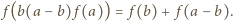
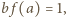 więc liczba po lewej stronie jest równa
więc liczba po lewej stronie jest równa 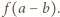 Prawa strona ma inną wartość, skoro
Prawa strona ma inną wartość, skoro 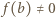 (wartości funkcji
(wartości funkcji 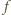 są z założenia niezerowe). Sprzeczność dowodzi, że
są z założenia niezerowe). Sprzeczność dowodzi, że 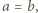 czyli
czyli 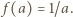 Wobec dowolności liczby
Wobec dowolności liczby 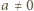 znaczy to, że funkcja
znaczy to, że funkcja 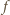 jest dana wzorem
jest dana wzorem 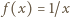 dla wszystkich
dla wszystkich 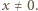 Sprawdzenie, że ta funkcja spełnia zadane równanie, jest natychmiastowe. Jest ona zatem jedynym rozwiązaniem tego równania.
Sprawdzenie, że ta funkcja spełnia zadane równanie, jest natychmiastowe. Jest ona zatem jedynym rozwiązaniem tego równania.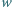 o współczynnikach całkowitych jest liczba
o współczynnikach całkowitych jest liczba 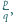 gdzie
gdzie 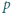 i
i 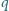 są względnie pierwszymi liczbami całkowitymi. Wykazać, że liczba
są względnie pierwszymi liczbami całkowitymi. Wykazać, że liczba 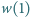 jest podzielna przez
jest podzielna przez 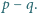
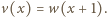 Wówczas liczba
Wówczas liczba 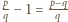 jest pierwiastkiem wielomianu
jest pierwiastkiem wielomianu 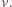 Niech
Niech 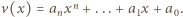 Wówczas po przemnożeniu obu stron równości
Wówczas po przemnożeniu obu stron równości 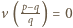 przez
przez 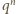 otrzymujemy
otrzymujemy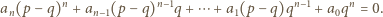
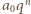 jest podzielna przez
jest podzielna przez 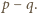 Ponieważ liczby
Ponieważ liczby 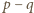 i
i 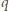 są względnie pierwsze, to wiemy, że
są względnie pierwsze, to wiemy, że 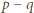 dzieli liczbę
dzieli liczbę 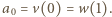
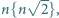 gdy
gdy 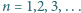
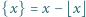 ).
).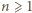 i oznaczmy
i oznaczmy 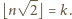 Oczywiście
Oczywiście 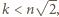 czyli
czyli 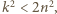 zatem
zatem 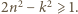 Dostajemy oszacowanie
Dostajemy oszacowanie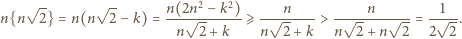
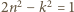 ; druga będzie "bliska równości", gdy stosunek
; druga będzie "bliska równości", gdy stosunek 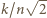 będzie bliski 1.
będzie bliski 1.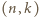 równania
równania 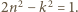 Para
Para 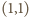 jest rozwiązaniem. Dalej, jeśli para
jest rozwiązaniem. Dalej, jeśli para 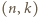 jest rozwiązaniem, to
jest rozwiązaniem, to 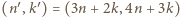 też, bowiem
też, bowiem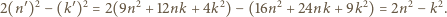
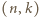 z dowolnie wielką wartością
z dowolnie wielką wartością 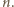 Gdy
Gdy 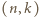 jest dowolną z takich par, wówczas
jest dowolną z takich par, wówczas 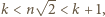 czyli
czyli 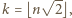 wobec czego (zgodnie z początkowym przekształceniem)
wobec czego (zgodnie z początkowym przekształceniem)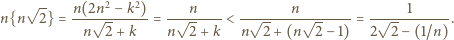
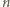 może być dowolnie wielka, zatem ostatnie wyrażenie może mieć wartość dowolnie bliską
może być dowolnie wielka, zatem ostatnie wyrażenie może mieć wartość dowolnie bliską 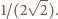 To dowodzi, że istotnie liczba
To dowodzi, że istotnie liczba 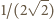 jest kresem dolnym zbioru wartości
jest kresem dolnym zbioru wartości 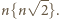
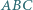 bok
bok 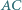 jest dłuższy niż
jest dłuższy niż 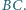 Punkt
Punkt 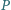 leży na dwusiecznej
leży na dwusiecznej 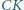 kąta
kąta 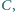 zaś punkt
zaś punkt 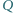 leży na środkowej
leży na środkowej 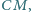 połowiącej bok
połowiącej bok 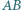 ; przy tym
; przy tym 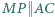 oraz
oraz 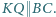 Wykazać, że odcinek
Wykazać, że odcinek 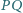 jest prostopadły do
jest prostopadły do 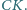
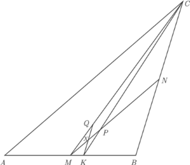
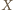 punkt przecięcia przekątnych czworokąta
punkt przecięcia przekątnych czworokąta 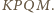 Prosta
Prosta 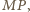 równoległa do
równoległa do 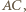 przecina bok
przecina bok 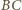 w punkcie
w punkcie 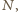 będącym środkiem tego boku. Skoro ów bok jest równoległy do
będącym środkiem tego boku. Skoro ów bok jest równoległy do 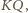 zatem punkt
zatem punkt 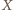 (leżący na prostej
(leżący na prostej 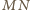 ) jest środkiem odcinka
) jest środkiem odcinka 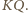
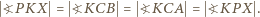
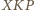 jest więc równoramienny:
jest więc równoramienny: 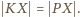 Punkt
Punkt 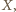 jako środek odcinka
jako środek odcinka 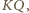 jest w takim razie środkiem okręgu opisanego na trójkącie
jest w takim razie środkiem okręgu opisanego na trójkącie 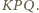 Wynika stąd, że kąt
Wynika stąd, że kąt 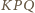 jest prosty - a to teza zadania.
jest prosty - a to teza zadania.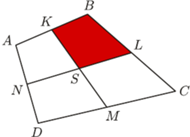
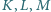 i
i 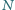 są odpowiednio środkami boków
są odpowiednio środkami boków 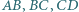 i
i 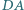 czworokąta wypukłego
czworokąta wypukłego 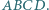 Odcinki
Odcinki 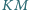 i
i 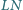 przecinają się w punkcie
przecinają się w punkcie 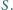 Znaleźć kres dolny i górny pola czworokąta
Znaleźć kres dolny i górny pola czworokąta 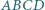 przy założeniu, że pole czworokąta
przy założeniu, że pole czworokąta 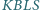 jest równe
jest równe 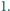
![|[ℱ]](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/1x-9dbfe84ebf61bac61555ddb19dc430d0032fb9e1-im-66,57,43-FF,FF,FF.gif) oznacza pole figury
oznacza pole figury 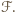
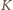 i
i 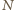 są środkami odcinków
są środkami odcinków 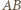 i
i 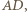 to
to 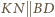 oraz
oraz 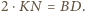 Podobnie otrzymujemy
Podobnie otrzymujemy 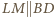 oraz
oraz 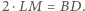 W takim razie czworokąt
W takim razie czworokąt 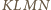 ma dwa boki równej długości i równoległe, więc jest równoległobokiem o środku
ma dwa boki równej długości i równoległe, więc jest równoległobokiem o środku 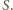 Ponadto trójkąt
Ponadto trójkąt 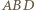 jest obrazem trójkąta
jest obrazem trójkąta 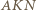 w jednokładności o środku
w jednokładności o środku 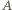 i skali
i skali 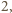 więc
więc ![]=4⋅[A].[AKBND](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/15x-89a4f3d2a354815ca7ee350824d02cb970519291-im-66,57,43-FF,FF,FF.gif) Z analogicznych rozważań dla trójkątów
Z analogicznych rozważań dla trójkątów 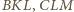 i
i 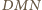 otrzymujemy
otrzymujemy![]+4⋅[BKL]+4⋅[C]+4⋅[DMN]=[ADB]+[BAC]+[CBD]+[DCA]=2⋅[ABCD].4L⋅[MAKN](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/18x-89a4f3d2a354815ca7ee350824d02cb970519291-dm-66,57,43-FF,FF,FF.gif)
![N]=8⋅[KLS]. [ABCD]](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/19x-89a4f3d2a354815ca7ee350824d02cb970519291-dm-66,57,43-FF,FF,FF.gif)
![4 ⋅[BKL] = [BAC]](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/20x-89a4f3d2a354815ca7ee350824d02cb970519291-dm-66,57,43-FF,FF,FF.gif)
![-1 [KBLS] = [KBL] + [KLS] ⩽ 4 [ABCD]](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/21x-89a4f3d2a354815ca7ee350824d02cb970519291-dm-66,57,43-FF,FF,FF.gif)
![1- [KBLS] ⩾ [KLS] = 8[ABCD].](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/22x-89a4f3d2a354815ca7ee350824d02cb970519291-dm-66,57,43-FF,FF,FF.gif)
![8-⩽ [ABCD] 3](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/23x-89a4f3d2a354815ca7ee350824d02cb970519291-dm-66,57,43-FF,FF,FF.gif)
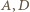 i
i 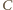 są współliniowe (wówczas
są współliniowe (wówczas ![[ABC] |](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/26x-89a4f3d2a354815ca7ee350824d02cb970519291-im-66,57,43-FF,FF,FF.gif) ), a maksimum - gdy wierzchołki
), a maksimum - gdy wierzchołki 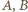 i
i 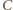 są współliniowe (wówczas
są współliniowe (wówczas ![|[ABC]](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-1512/29x-89a4f3d2a354815ca7ee350824d02cb970519291-im-66,57,43-FF,FF,FF.gif) ).
).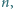 dla których liczba
dla których liczba 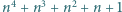 jest kwadratem liczby całkowitej.
jest kwadratem liczby całkowitej.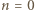 spełnia warunki zadania i załóżmy teraz, że
spełnia warunki zadania i załóżmy teraz, że 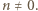 Wówczas
Wówczas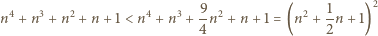
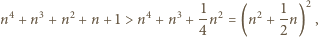
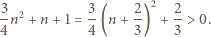
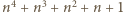 leży wewnątrz przedziału
leży wewnątrz przedziału 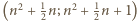 długości
długości 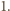 Jeśli
Jeśli 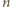 jest liczbą parzystą, to końce przedziału są liczbami całkowitymi i
jest liczbą parzystą, to końce przedziału są liczbami całkowitymi i  nie może spełniać warunków zadania. W przeciwnym razie wewnątrz przedziału leży dokładnie jedna liczba całkowita
nie może spełniać warunków zadania. W przeciwnym razie wewnątrz przedziału leży dokładnie jedna liczba całkowita 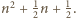 Pozostaje sprawdzić, dla jakich liczb
Pozostaje sprawdzić, dla jakich liczb 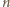 zachodzi równość
zachodzi równość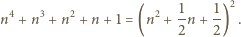
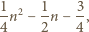
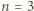 i
i 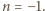 Łatwo sprawdzić, że obie te liczby spełniają warunki zadania.
Łatwo sprawdzić, że obie te liczby spełniają warunki zadania.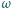 losujemy 11 punktów (przy losowaniu każdy punkt koła jest jednakowo prawdopodobny). Znaleźć prawdopodobieństwo tego, że istnieje taka średnica koła
losujemy 11 punktów (przy losowaniu każdy punkt koła jest jednakowo prawdopodobny). Znaleźć prawdopodobieństwo tego, że istnieje taka średnica koła 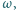 iż wszystkie wylosowane punkty leżą po tej samej jej stronie. Ponieważ prawdopodobieństwo wylosowania dwóch punktów leżących na tej samej średnicy koła
iż wszystkie wylosowane punkty leżą po tej samej jej stronie. Ponieważ prawdopodobieństwo wylosowania dwóch punktów leżących na tej samej średnicy koła 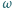 jest równe zeru, możemy założyć, że taka sytuacja się nie zdarzyła.
jest równe zeru, możemy założyć, że taka sytuacja się nie zdarzyła.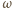 jest równe zeru, możemy założyć, że taka sytuacja się nie zdarzyła.
jest równe zeru, możemy założyć, że taka sytuacja się nie zdarzyła.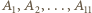 będą pewnymi punktami koła
będą pewnymi punktami koła 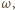 a
a 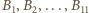 - punktami symetrycznymi do nich względem środka koła. Rozważmy
- punktami symetrycznymi do nich względem środka koła. Rozważmy 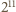 sytuacji, w których dla każdego
sytuacji, w których dla każdego 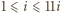 -tym wylosowanym punktem jest
-tym wylosowanym punktem jest 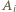 lub
lub 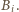 Wśród nich jest
Wśród nich jest 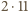 takich przypadków, w których wylosowane punkty leżą po jednej stronie pewnej średnicy koła
takich przypadków, w których wylosowane punkty leżą po jednej stronie pewnej średnicy koła 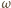 - każdy odpowiada wyborowi pewnego punktu spośród wyróżnionych oraz
- każdy odpowiada wyborowi pewnego punktu spośród wyróżnionych oraz 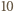 "kolejnych" zgodnie z ruchem wskazówek zegara.
"kolejnych" zgodnie z ruchem wskazówek zegara.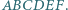 Każda z przekątnych
Każda z przekątnych 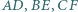 dzieli ten sześciokąt na dwa czworokąty o równych polach. Udowodnij, że przekątne te przecinają się w jednym punkcie.
dzieli ten sześciokąt na dwa czworokąty o równych polach. Udowodnij, że przekątne te przecinają się w jednym punkcie.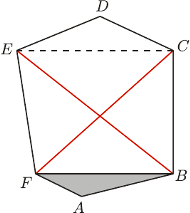
![[ℱ]](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-16_11-deltoid-2/1x-f0947e5fa2249f537e09dae26bfbbda96a771afe-im-66,57,43-FF,FF,FF.gif) oznacza pole figury
oznacza pole figury 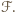 Skoro
Skoro ![1 |[BACF] = 2[BACDEF] = [ABEF],](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-16_11-deltoid-2/3x-f0947e5fa2249f537e09dae26bfbbda96a771afe-im-66,57,43-FF,FF,FF.gif) to
to ![|[FBC] = [FBE].](/math/temat/matematyka/geometria/planimetria/zadania/2016/10/31/zm-16_11-deltoid-2/4x-f0947e5fa2249f537e09dae26bfbbda96a771afe-im-66,57,43-FF,FF,FF.gif) Trójkąty te mają wspólną podstawę
Trójkąty te mają wspólną podstawę 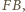 zatem mają też równe wysokości na nią. Ponieważ punkty
zatem mają też równe wysokości na nią. Ponieważ punkty 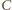 i
i 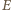 leżą po tej samej stronie prostej
leżą po tej samej stronie prostej 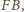 wynika stąd, że
wynika stąd, że 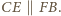 Analogicznie
Analogicznie 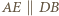 oraz
oraz 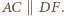
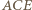 i
i 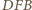 spełniają założenia twierdzenia
spełniają założenia twierdzenia 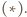 Jeden z nich jest więc obrazem drugiego w pewnej jednokładności o ujemnej skali, której środek leży na każdym z odcinków
Jeden z nich jest więc obrazem drugiego w pewnej jednokładności o ujemnej skali, której środek leży na każdym z odcinków 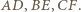
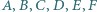
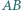
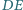
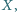
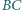
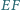
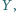
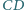
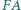
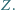
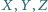
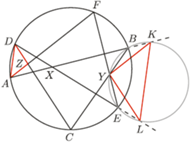
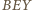 przecina proste
przecina proste 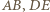 w drugich punktach odpowiednio
w drugich punktach odpowiednio 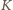 i
i  Dowód przeprowadzimy w przypadku przedstawionym na rysunku, pozostałe można uzasadnić podobnie.
Dowód przeprowadzimy w przypadku przedstawionym na rysunku, pozostałe można uzasadnić podobnie. i
i  Z równości kątów wpisanych opartych na jednym łuku mamy
Z równości kątów wpisanych opartych na jednym łuku mamy 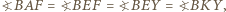 więc
więc 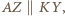 ponieważ punkty
ponieważ punkty 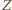 i
i 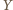 leżą po przeciwnych stronach prostej
leżą po przeciwnych stronach prostej 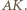 Podobnie
Podobnie 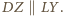 Ponadto czworokąt
Ponadto czworokąt 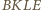 jest wpisany w okrąg, zatem
jest wpisany w okrąg, zatem 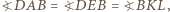 a stąd
a stąd 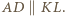
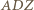 i
i 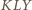 spełniają założenia twierdzenia
spełniają założenia twierdzenia 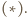 Stąd punkt
Stąd punkt 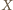 przecięcia prostych
przecięcia prostych 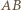 i
i 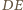 należy też do prostej
należy też do prostej 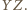
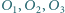 są styczne odpowiednio do par boków
są styczne odpowiednio do par boków 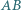 i
i 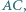
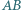 i
i 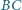 oraz
oraz 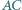 i
i 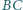 trójkąta
trójkąta 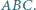 Okrąg
Okrąg 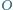 jest styczny zewnętrznie do okręgów
jest styczny zewnętrznie do okręgów 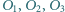 odpowiednio w punktach
odpowiednio w punktach 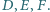 Wykaż, że proste
Wykaż, że proste 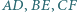 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.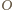 trójkąt
trójkąt 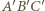 o bokach odpowiednio równoległych do boków trójkąta
o bokach odpowiednio równoległych do boków trójkąta 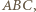 ale niezgodnie ułożony, a następnie dowieść, że pewna jednokładność o środku
ale niezgodnie ułożony, a następnie dowieść, że pewna jednokładność o środku 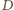 przeprowadza punkt
przeprowadza punkt 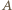 na
na 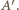
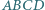 oraz punkt
oraz punkt 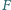 leżący na odcinku
leżący na odcinku 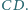 Punkty
Punkty 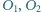 i
i 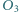 są środkami okręgów opisanych na trójkątach
są środkami okręgów opisanych na trójkątach 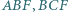 i
i 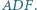 Dowieść, że ortocentrum trójkąta
Dowieść, że ortocentrum trójkąta 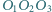 leży na prostej
leży na prostej 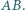
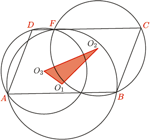
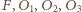 leżą na jednym okręgu. Istotnie,
leżą na jednym okręgu. Istotnie,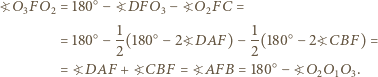
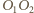 i
i 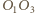 są prostopadłe odpowiednio do
są prostopadłe odpowiednio do 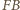 i
i 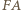 ). Na podstawie twierdzenia Steinera pozostaje uzasadnić, że odbicia punktu
). Na podstawie twierdzenia Steinera pozostaje uzasadnić, że odbicia punktu 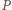 względem boków trójkąta
względem boków trójkąta 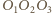 leżą na prostej
leżą na prostej 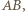 jednakże jest to oczywiste, gdyż proste
jednakże jest to oczywiste, gdyż proste 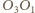 oraz
oraz 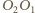 są symetralnymi odcinków odpowiednio
są symetralnymi odcinków odpowiednio 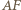 i
i 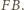
 opisanym na okręgu prosta
opisanym na okręgu prosta  przechodząca przez wierzchołek
przechodząca przez wierzchołek  przecina bok
przecina bok  w punkcie
w punkcie 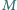 oraz półprostą
oraz półprostą 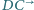 w punkcie
w punkcie 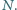 Punkty
Punkty 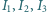 są środkami okręgów wpisanych odpowiednio w trójkąty
są środkami okręgów wpisanych odpowiednio w trójkąty 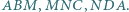 Dowieść, że punkt przecięcia wysokości trójkąta
Dowieść, że punkt przecięcia wysokości trójkąta 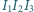 leży na prostej
leży na prostej 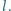
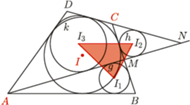
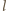 przecina półprostą
przecina półprostą 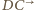 w punkcie
w punkcie 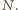 Trójki punktów
Trójki punktów 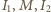 oraz
oraz 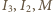 są, oczywiście, współliniowe. Oznaczmy przez
są, oczywiście, współliniowe. Oznaczmy przez 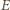 przecięcie prostych
przecięcie prostych 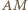 i drugiej stycznej poprowadzonej z punktu
i drugiej stycznej poprowadzonej z punktu 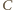 do okręgu o środku w punkcie
do okręgu o środku w punkcie 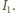 Łatwo zauważyć, że
Łatwo zauważyć, że 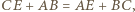 więc
więc 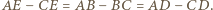 Oznacza to, że półprosta
Oznacza to, że półprosta 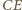 jest również styczna do okręgu o środku w punkcie
jest również styczna do okręgu o środku w punkcie 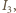 stąd punkty
stąd punkty 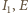 i
i 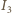 są współliniowe. Wobec tego
są współliniowe. Wobec tego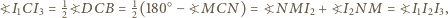
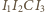 można opisać okrąg. Aby dokończyć rozwiązanie, wystarczy zauważyć, że obrazy punktu
można opisać okrąg. Aby dokończyć rozwiązanie, wystarczy zauważyć, że obrazy punktu 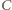 w symetrii względem prostych
w symetrii względem prostych 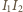 oraz
oraz 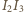 leżą na prostej
leżą na prostej 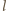 i zastosować twierdzenie Steinera.
i zastosować twierdzenie Steinera.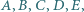 takie, że czworokąt
takie, że czworokąt 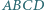 jest równoległobokiem, a czworokąt
jest równoległobokiem, a czworokąt 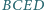 jest wpisany w okrąg. Prosta
jest wpisany w okrąg. Prosta 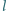 przechodząca przez
przechodząca przez 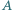 przecina wnętrze odcinka
przecina wnętrze odcinka 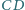 w punkcie
w punkcie 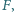 a prostą
a prostą 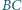 w punkcie
w punkcie 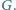 Przypuśćmy, że
Przypuśćmy, że 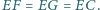 Wykazać, że
Wykazać, że 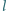 jest dwusieczną kąta
jest dwusieczną kąta