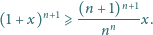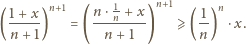Kąty trójścienne»Zadanie 6
o zadaniu...
- Zadanie pochodzi z artykułu Kąty trójścienne
- Publikacja w Delcie: grudzień 2013
- Publikacja elektroniczna: 01-12-2013
- Artykuł źródłowy w wersji do druku [application/pdf]: (62 KB)
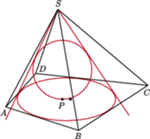
Czy istnieje taki ostrosłup czworokątny
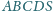 o podstawie
o podstawie
 w którym
w którym
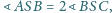
 oraz
oraz
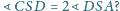

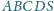 o podstawie czworokąta
wypukłego
o podstawie czworokąta
wypukłego
 Sfera wpisana w ten ostrosłup jest styczna do ściany
Sfera wpisana w ten ostrosłup jest styczna do ściany
 w punkcie
w punkcie
 Dowieść, że
Dowieść, że
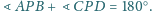
 będzie stożkiem o wierzchołku
będzie stożkiem o wierzchołku
 w który wpisana jest
sfera wpisana w ostrosłup
w który wpisana jest
sfera wpisana w ostrosłup
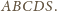 Część wspólna tego stożka
z płaszczyzną podstawy jest elipsą wpisaną w czworokąt
Część wspólna tego stożka
z płaszczyzną podstawy jest elipsą wpisaną w czworokąt
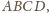 a punkt
a punkt
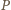 jest jej ogniskiem. Teza zadania jest po prostu jedną ze znanych
własności elipsy wpisanej w czworokąt.
jest jej ogniskiem. Teza zadania jest po prostu jedną ze znanych
własności elipsy wpisanej w czworokąt.
 jest styczna do ścian
jest styczna do ścian
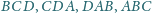 odpowiednio w punktach
odpowiednio w punktach
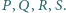 Odcinek
Odcinek
 jest średnicą tej sfery, a punkty
jest średnicą tej sfery, a punkty
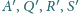 są punktami
przecięcia prostych
są punktami
przecięcia prostych
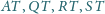 z płaszczyzną
z płaszczyzną
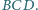 Dowieść,
że punkt
Dowieść,
że punkt
 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie
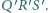

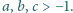
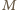 będzie średnią arytmetyczną liczb
będzie średnią arytmetyczną liczb
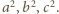 Oznaczmy:
Oznaczmy:
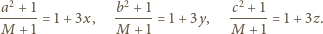
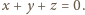 Stąd
Stąd
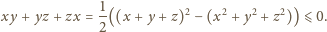
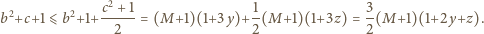
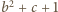 jest dodatnia (tu korzystamy z założenia, że
jest dodatnia (tu korzystamy z założenia, że
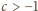 ), zatem po prawej stronie ostatniej nierówności mamy również
liczbę dodatnią, i wobec tego
), zatem po prawej stronie ostatniej nierówności mamy również
liczbę dodatnią, i wobec tego
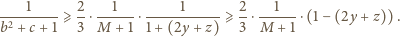

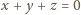 oraz
oraz
 ):
):
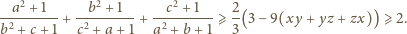
 okrąg wpisany jest styczny do boków
okrąg wpisany jest styczny do boków
 odpowiednio w punktach
odpowiednio w punktach
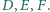 Punkty
Punkty
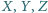 zostały obrane odpowiednio na bokach
zostały obrane odpowiednio na bokach
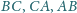 tak,
że
tak,
że
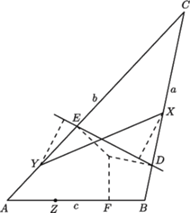
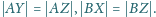 Dowieść, że prosta
Dowieść, że prosta
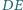 połowi
odcinek
połowi
odcinek

 Równości
Równości
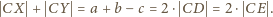
 i
i
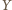 leżą po przeciwnych stronach
prostej
leżą po przeciwnych stronach
prostej
 w jednakowych odległościach od odpowiednich końców
odcinka
w jednakowych odległościach od odpowiednich końców
odcinka
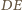 :
:

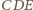 oznacza to z kolei, że
punkty
oznacza to z kolei, że
punkty
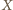 i
i
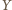 leżą w jednakowych odległościach od prostej
leżą w jednakowych odległościach od prostej
 Stąd już wynika, że ta prosta przechodzi przez środek odcinka
Stąd już wynika, że ta prosta przechodzi przez środek odcinka
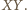
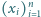 liczb rzeczywistych
dodatnich prawdziwa jest nierówność
liczb rzeczywistych
dodatnich prawdziwa jest nierówność
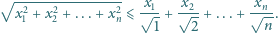
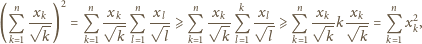
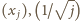 są malejące.
są malejące.
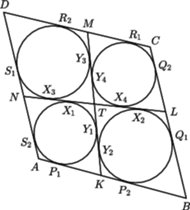
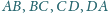 czworokąta wypukłego
czworokąta wypukłego
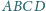 dane są
odpowiednio punkty
dane są
odpowiednio punkty
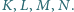 Odcinki
Odcinki
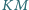 i
i
 przecinają
się w punkcie
przecinają
się w punkcie
 Udowodnić, że jeśli w każdy z czworokątów
Udowodnić, że jeśli w każdy z czworokątów
 można wpisać okrąg, to w czworokąt
można wpisać okrąg, to w czworokąt
 także.
także.
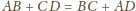 jest
równoważny
jest
równoważny
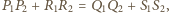 gdyż
gdyż
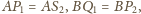
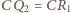 i
i
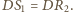 Zauważmy, że
Zauważmy, że
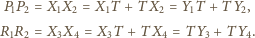
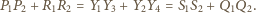
 prawdziwa jest nierówność
prawdziwa jest nierówność
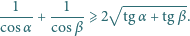
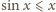 mamy
mamy
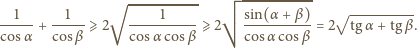
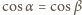 i
i
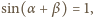 co jest równoważne temu, że
co jest równoważne temu, że
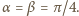
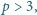 taka, że
taka, że
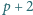 też jest pierwsza.
Na tablicy napisano liczby
też jest pierwsza.
Na tablicy napisano liczby
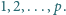 W każdym kroku wybieramy
jedną z nich, powiedzmy
W każdym kroku wybieramy
jedną z nich, powiedzmy
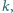 po czym zmazujemy wszystkie dzielniki
liczby
po czym zmazujemy wszystkie dzielniki
liczby
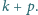 Udowodnić, że w ten sposób nigdy nie zmażemy
wszystkich liczb napisanych na tablicy.
Udowodnić, że w ten sposób nigdy nie zmażemy
wszystkich liczb napisanych na tablicy.
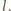 Skoro została ona zmazana, to
Skoro została ona zmazana, to
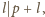 czyli również
czyli również
 a zatem
a zatem
 lub
lub

 i
i
 będą odpowiednio liczbami wybranymi w pierwszym i drugim kroku.
Ponieważ liczba 1 zniknęła z tablicy po pierwszym kroku, więc
będą odpowiednio liczbami wybranymi w pierwszym i drugim kroku.
Ponieważ liczba 1 zniknęła z tablicy po pierwszym kroku, więc
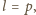 co oznacza, że po pierwszym kroku na tablicy były wyłącznie liczby
co oznacza, że po pierwszym kroku na tablicy były wyłącznie liczby
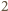 i
i
 lub tylko
lub tylko
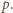 Ponieważ
Ponieważ
 więc
więc
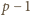 zmazaliśmy w pierwszym kroku, a zatem
zmazaliśmy w pierwszym kroku, a zatem
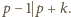 Natomiast z nierówności
Natomiast z nierówności
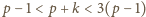 wynika, że
wynika, że
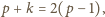 czyli
czyli
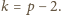 Ale
Ale
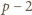 też musiało
zostać zmazane w pierwszym kroku, więc
też musiało
zostać zmazane w pierwszym kroku, więc
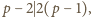 co jest
niemożliwe.
co jest
niemożliwe.
 Ta liczba nie została zmazana w tym
kroku, gdyż
Ta liczba nie została zmazana w tym
kroku, gdyż
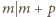 oznacza, że
oznacza, że
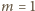 lub
lub
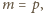 ale 1
zniknęła w pierwszym kroku, a
ale 1
zniknęła w pierwszym kroku, a
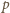 musi być wybrane w ostatnim. Zatem
musi być wybrane w ostatnim. Zatem
 zmazujemy w ostatnim kroku, czyli
zmazujemy w ostatnim kroku, czyli
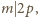 więc
więc
 Wobec tego w przedostatnim kroku mogliśmy wymazać tylko dzielniki liczby
Wobec tego w przedostatnim kroku mogliśmy wymazać tylko dzielniki liczby
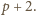 Ale ta liczba jest pierwsza, więc nie wymazaliśmy nic, co daje
sprzeczność.
Ale ta liczba jest pierwsza, więc nie wymazaliśmy nic, co daje
sprzeczność.
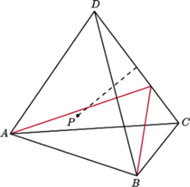
 leży wewnątrz czworościanu
leży wewnątrz czworościanu
 Przez każdą
krawędź tego czworościanu prowadzimy płaszczyznę równoległą do prostej
łączącej punkt
Przez każdą
krawędź tego czworościanu prowadzimy płaszczyznę równoległą do prostej
łączącej punkt
 ze środkiem przeciwległej krawędzi. Wykazać, że
istnieje punkt wspólny otrzymanych sześciu płaszczyzn.
ze środkiem przeciwległej krawędzi. Wykazać, że
istnieje punkt wspólny otrzymanych sześciu płaszczyzn.
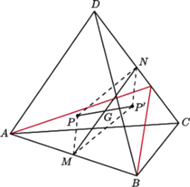
 punktu
punktu
 względem
środka ciężkości
względem
środka ciężkości
 danego czworościanu należy do każdej
z sześciu rozważanych płaszczyzn. Wystarczy, że udowodnimy, iż punkt
danego czworościanu należy do każdej
z sześciu rozważanych płaszczyzn. Wystarczy, że udowodnimy, iż punkt
 należy do płaszczyzny
należy do płaszczyzny
 przechodzącej przez punkty
przechodzącej przez punkty
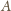 i
i
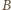 oraz równoległej do prostej łączącej punkt
oraz równoległej do prostej łączącej punkt
 ze
środkiem krawędzi
ze
środkiem krawędzi
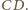
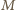 i
i
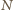 będą środkami krawędzi
będą środkami krawędzi
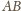 i
i
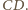 Punkt
Punkt
 jest środkiem odcinka
jest środkiem odcinka
 a więc czworokąt
a więc czworokąt
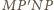 jest
równoległobokiem. Zatem proste
jest
równoległobokiem. Zatem proste
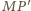 i
i
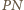 są równoległe. Skoro
punkt
są równoległe. Skoro
punkt
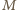 leży w płaszczyźnie
leży w płaszczyźnie
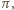 to prosta
to prosta
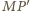 także.
To dowodzi, że punkt
także.
To dowodzi, że punkt
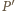 należy do płaszczyzny
należy do płaszczyzny
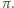
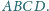 Odcinki
Odcinki
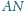 i
i
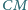 są
dwusiecznymi w trójkącie
są
dwusiecznymi w trójkącie
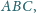 odcinek
odcinek
 jest dwusieczną
w trójkącie
jest dwusieczną
w trójkącie
 zaś odcinek
zaś odcinek
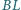 jest dwusieczną
w trójkącie
jest dwusieczną
w trójkącie
 Wykazać, że istnieje punkt wspólny płaszczyzn
Wykazać, że istnieje punkt wspólny płaszczyzn
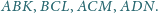
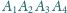 i punkty
i punkty
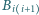 leżące na
krawędziach
leżące na
krawędziach
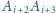 dla
dla
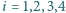 przyjmujemy, że
przyjmujemy, że
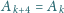 ). Każda z płaszczyzn
). Każda z płaszczyzn
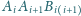 tworzy z płaszczyzną
tworzy z płaszczyzną
 kąt dwuścienny o mierze
kąt dwuścienny o mierze
 zaś z płaszczyzną
zaś z płaszczyzną
 kąt dwuścienny o mierze
kąt dwuścienny o mierze
 Wykazać, że
płaszczyzny
Wykazać, że
płaszczyzny
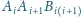 dla
dla
 mają wspólny punkt
wtedy i tylko wtedy, gdy
mają wspólny punkt
wtedy i tylko wtedy, gdy
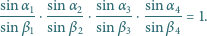
 leży wewnątrz czworościanu
leży wewnątrz czworościanu
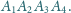 Wykazać, że
płaszczyzny symetryczne do płaszczyzn
Wykazać, że
płaszczyzny symetryczne do płaszczyzn
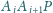 względem płaszczyzn
dwusiecznych kątów dwuściennych przy krawędziach
względem płaszczyzn
dwusiecznych kątów dwuściennych przy krawędziach
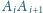 dla
dla
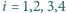 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
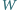 będzie wielomianem stopnia
będzie wielomianem stopnia
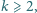 o współczynnikach
całkowitych nieujemnych. Zakładamy, że dla każdej liczby naturalnej
o współczynnikach
całkowitych nieujemnych. Zakładamy, że dla każdej liczby naturalnej
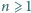 wartość
wartość
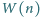 jest
jest
 -tą potęgą liczby całkowitej
nieujemnej. Udowodnić, że
-tą potęgą liczby całkowitej
nieujemnej. Udowodnić, że
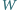 ma postać
ma postać
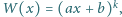 gdzie
gdzie
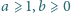 są liczbami całkowitymi.
są liczbami całkowitymi.
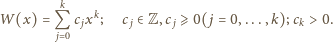
 taki,
że
taki,
że
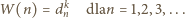
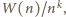 czyli
czyli
 dąży do
dąży do
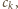 gdy
gdy
 Stąd
Stąd
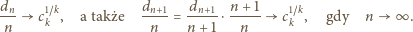
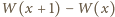 jest wielomianem stopnia
jest wielomianem stopnia
 z wyrazem
wiodącym
z wyrazem
wiodącym
 Zatem
Zatem
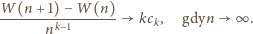
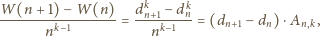
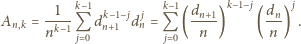
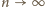 mamy
mamy
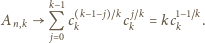
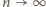
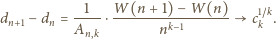
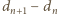 przedstawia więc ciąg liczb całkowitych, który jest
zbieżny – taki ciąg jest od pewnego miejsca stały. Oznaczając
przedstawia więc ciąg liczb całkowitych, który jest
zbieżny – taki ciąg jest od pewnego miejsca stały. Oznaczając
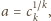 mamy
zatem
mamy
zatem
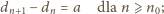
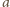 jest całkowita oraz dodatnia.
jest całkowita oraz dodatnia.
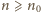 uzyskujemy równość
uzyskujemy równość
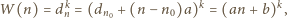
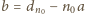 jest liczbą całkowitą.
jest liczbą całkowitą.
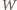 jest wielomianem
jest wielomianem
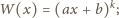
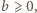 skoro (z założenia)
współczynniki
skoro (z założenia)
współczynniki
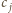 wielomianu
wielomianu
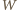 są nieujemne, zaś
są nieujemne, zaś

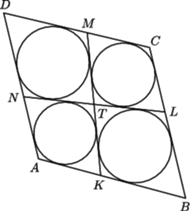
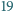 osób. Na ostatnich dwóch treningach
wszyscy zawodnicy byli obecni i na każdym z nich podzielono ich na trzy
zespoły: dwa sześcioosobowe i jeden siedmioosobowy. Udowodnić, że
można wskazać
osób. Na ostatnich dwóch treningach
wszyscy zawodnicy byli obecni i na każdym z nich podzielono ich na trzy
zespoły: dwa sześcioosobowe i jeden siedmioosobowy. Udowodnić, że
można wskazać
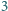 osoby, które na obu treningach były w jednej
drużynie.
osoby, które na obu treningach były w jednej
drużynie.
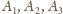 to podzbiory zbioru
to podzbiory zbioru
 oznaczające składy drużyn na pierwszym treningu, a
oznaczające składy drużyn na pierwszym treningu, a
 –
na drugim. Chcemy udowodnić, że dla pewnych
–
na drugim. Chcemy udowodnić, że dla pewnych
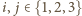 mamy
mamy
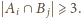 Przypuśćmy, że nie ma takiej pary zbiorów.
Ponieważ
Przypuśćmy, że nie ma takiej pary zbiorów.
Ponieważ
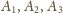 są parami rozłączne i
są parami rozłączne i
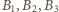 także, więc
mamy
także, więc
mamy
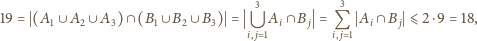
 i liczby całkowitej
i liczby całkowitej
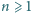 prawdziwa jest nierówność
prawdziwa jest nierówność