Klub 44M - zadania XI 2020»Zadanie 810
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania XI 2020
- Publikacja w Delcie: listopad 2020
- Publikacja elektroniczna: 1 listopada 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (364 KB)
-
Zadanie 810 zaproponował pan Semen Słobodianiuk.
Dla permutacji 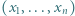 zbioru
zbioru 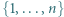 rozważamy liczby:
rozważamy liczby:
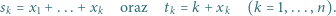 |
Dla każdej liczby naturalnej 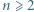 udowodnić, że permutacja o własności:
udowodnić, że permutacja o własności:
- (i)
- liczby
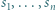 dają różne reszty z dzielenia przez
dają różne reszty z dzielenia przez 
istnieje wtedy i tylko wtedy, gdy nie istnieje permutacja o własności:
- (ii)
- liczby
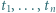 dają różne reszty z dzielenia przez
dają różne reszty z dzielenia przez 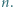
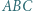
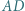
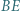
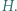
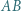
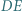
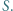
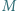
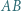
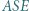
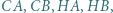
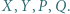
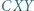
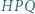
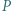
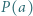
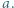

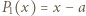
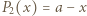
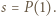
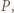
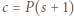 ; reprezentacja tej liczby w
; reprezentacja tej liczby w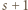
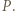

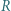
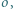
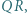
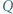
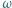
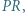

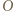
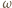
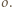
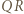
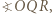
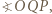
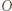
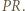
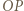
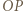
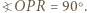
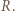
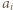
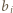
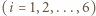 , to prawdopodobieństwo uzyskania sumy oczek równej
, to prawdopodobieństwo uzyskania sumy oczek równej 
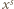
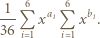
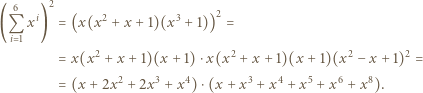
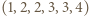
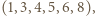
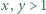
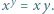
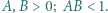
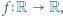
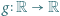
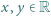

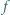
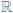
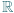 ; ma więc funkcję odwrotną
; ma więc funkcję odwrotną 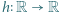
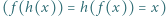 . Udowodnić, że funkcja
. Udowodnić, że funkcja 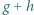
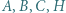
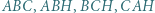
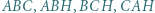
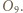
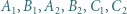
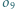
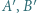
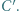
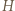 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 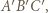 a dwusieczne kątów wewnętrznych i zewnętrznych przecinają okrąg opisany na trójkącie w środkach odpowiednich łuków (zob. kącik nr 3).
a dwusieczne kątów wewnętrznych i zewnętrznych przecinają okrąg opisany na trójkącie w środkach odpowiednich łuków (zob. kącik nr 3).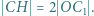
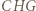 i
i 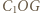 są podobne (kk).
są podobne (kk).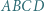
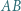
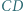
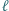
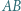
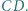
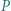
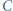
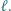
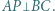
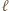 jest prostą Eulera trójkąta
jest prostą Eulera trójkąta 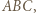 bo leży na niej środek ciężkości i środek okręgu opisanego na tym trójkącie. Punkt
bo leży na niej środek ciężkości i środek okręgu opisanego na tym trójkącie. Punkt 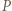 jest ortocentrum trójkąta
jest ortocentrum trójkąta 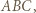 gdyż leży on na jego prostej Eulera oraz na wysokości poprowadzonej z wierzchołka
gdyż leży on na jego prostej Eulera oraz na wysokości poprowadzonej z wierzchołka 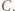
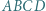
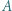
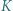
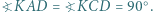
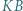
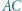
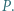
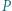
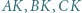
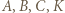 tworzą układ ortocentryczny, gdyż
tworzą układ ortocentryczny, gdyż 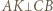 i
i 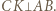
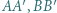
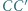
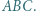
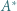
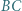
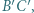
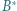
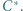
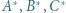
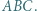
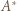 względem okręgów:
względem okręgów: 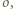 okręgu o średnicy
okręgu o średnicy 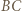 oraz
oraz 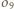 są równe, więc punkt
są równe, więc punkt 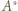 leży na osi potęgowej okręgów
leży na osi potęgowej okręgów  i
i 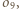 czyli prostej prostopadłej do
czyli prostej prostopadłej do 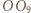 (prostej Eulera). Analogicznie postępujemy z punktami
(prostej Eulera). Analogicznie postępujemy z punktami 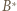 i
i 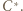 (O potędze punktu względem okręgu można przeczytać w kąciku nr 11).
(O potędze punktu względem okręgu można przeczytać w kąciku nr 11).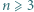 różnych liczb rzeczywistych, przy czym
różnych liczb rzeczywistych, przy czym  jest liczbą nieparzystą. Dla każdej pary
jest liczbą nieparzystą. Dla każdej pary 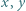 liczb z tablicy na osobnej karteczce zapisano liczbę
liczb z tablicy na osobnej karteczce zapisano liczbę 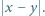 Wykazać, że wszystkie karteczki można podzielić na dwa stosy o równych sumach zapisanych liczb.
Wykazać, że wszystkie karteczki można podzielić na dwa stosy o równych sumach zapisanych liczb.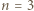 niech
niech 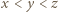 będą elementami zbioru
będą elementami zbioru 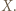 Wówczas na jednym stosie kładziemy karteczkę z liczbą
Wówczas na jednym stosie kładziemy karteczkę z liczbą 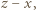 a na drugim - karteczki z liczbami
a na drugim - karteczki z liczbami 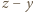 oraz
oraz 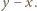
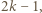 i rozważmy dowolny zbiór
i rozważmy dowolny zbiór 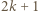 liczb
liczb 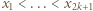 oraz związane z nimi karteczki. Z założenia indukcyjnego wszystkie karteczki pochodzące wyłącznie od liczb
oraz związane z nimi karteczki. Z założenia indukcyjnego wszystkie karteczki pochodzące wyłącznie od liczb 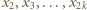 można podzielić na stosy o równych sumach. Pozostałe karteczki najpierw podzielmy na następujące
można podzielić na stosy o równych sumach. Pozostałe karteczki najpierw podzielmy na następujące 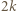 grup:
grup: 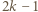 grup po dwie karteczki, z liczbami
grup po dwie karteczki, z liczbami 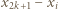 oraz
oraz 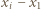 dla
dla 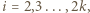 oraz jedna grupa składająca się z pozostałej karteczki z liczbą
oraz jedna grupa składająca się z pozostałej karteczki z liczbą 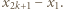 Zauważmy, że w każdej grupie suma liczb z karteczek jest równa
Zauważmy, że w każdej grupie suma liczb z karteczek jest równa 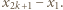 Wobec tego wystarczy karteczki z dowolnych
Wobec tego wystarczy karteczki z dowolnych 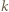 grup dołączyć do jednego stosu, a karteczki z pozostałych
grup dołączyć do jednego stosu, a karteczki z pozostałych 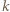 grup - do drugiego stosu. To kończy dowód indukcyjny.
grup - do drugiego stosu. To kończy dowód indukcyjny.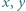 liczb z tablicy na osobnej karteczce zapisano liczbę
liczb z tablicy na osobnej karteczce zapisano liczbę 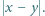 Czy może się zdarzyć, że na karteczkach zapisano liczby całkowite od 1 do 10?
Czy może się zdarzyć, że na karteczkach zapisano liczby całkowite od 1 do 10?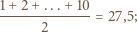
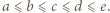 Wówczas najmniejsza z liczb zapisanych na karteczkach to
Wówczas najmniejsza z liczb zapisanych na karteczkach to 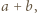 druga najmniejsza (być może równa) -
druga najmniejsza (być może równa) - 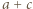 ; największa to
; największa to  a druga największa -
a druga największa - 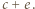 Ponadto sumując liczby ze wszystkich karteczek, uzyskujemy
Ponadto sumując liczby ze wszystkich karteczek, uzyskujemy 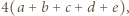 a zatem znamy również wartość
a zatem znamy również wartość 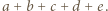 Ta wiedza wystarcza kolejno do znalezienia wartości
Ta wiedza wystarcza kolejno do znalezienia wartości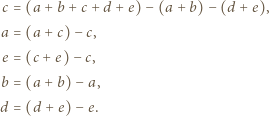
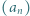 jest określony wzorami
jest określony wzorami 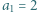 ;
; 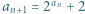 dla
dla 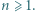 Niech
Niech 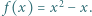 Udowodnić, że dla każdego
Udowodnić, że dla każdego 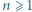 liczba
liczba 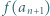 dzieli się przez
dzieli się przez 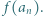
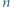 -kąta
-kąta 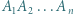 leży taki punkt
leży taki punkt 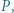 że każdy z trójkątów
że każdy z trójkątów 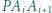 jest równoramienny (przyjmujemy
jest równoramienny (przyjmujemy 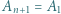 ). Czy stąd wynika, że wielokąt ma okrąg opisany, którego środkiem jest punkt
). Czy stąd wynika, że wielokąt ma okrąg opisany, którego środkiem jest punkt 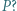
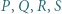 tworzą układ ortocentryczny, to:
tworzą układ ortocentryczny, to: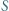 względem prostej
względem prostej 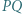 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 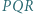 ;
;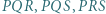 i
i 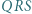 mają równe promienie;
mają równe promienie;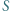 względem środka odcinka
względem środka odcinka 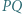 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 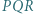 ;
;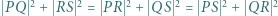 ;
;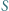 jest środkiem okręgu wpisanego lub dopisanego do trójkąta utworzonego przez spodki układu.
jest środkiem okręgu wpisanego lub dopisanego do trójkąta utworzonego przez spodki układu.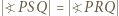 lub
lub 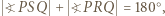 w zależności od umiejscowienia punktu
w zależności od umiejscowienia punktu 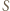 względem pozostałych.
względem pozostałych.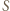 i
i 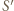 są symetryczne względem prostej
są symetryczne względem prostej 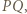 to okręgi opisane na trójkątach
to okręgi opisane na trójkątach 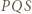 i
i 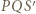 również. Wystarczy skorzystać z poprzedniego podpunktu.
również. Wystarczy skorzystać z poprzedniego podpunktu.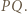
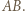 Okrąg o średnicy
Okrąg o średnicy 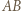 przecina proste
przecina proste 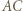 i
i 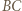 w punktach, które są spodkami wysokości trójkąta
w punktach, które są spodkami wysokości trójkąta 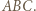
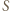 wewnątrz i na zewnątrz trójkąta
wewnątrz i na zewnątrz trójkąta 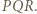 Do rachunków na kątach wykorzystać okręgi, o których była mowa we wstępie.
Do rachunków na kątach wykorzystać okręgi, o których była mowa we wstępie.