Równoległobok»Zadanie 7
o zadaniu...
- Zadanie pochodzi z artykułu Równoległobok
- Publikacja w Delcie: czerwiec 2020
- Publikacja elektroniczna: 31 maja 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (346 KB)
Niech 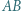 będzie krótszym łukiem okręgu
będzie krótszym łukiem okręgu 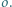 Na łuku
Na łuku 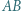 wybieramy punkt
wybieramy punkt 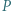 różny od
różny od 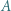 i
i 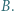 Punkt
Punkt 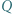 leży na prostej
leży na prostej 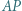 i spełnia równość
i spełnia równość 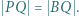 Punkt
Punkt 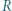 leży na prostej
leży na prostej 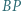 i spełnia warunek
i spełnia warunek 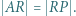 Wreszcie punkt
Wreszcie punkt 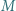 jest środkiem odcinka
jest środkiem odcinka 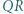 i przez
i przez 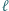 oznaczamy prostą
oznaczamy prostą 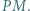 Dowieść, że wszystkie otrzymane w ten sposób proste
Dowieść, że wszystkie otrzymane w ten sposób proste 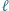 (dla różnych punktów
(dla różnych punktów 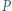 ) mają punkt wspólny.
) mają punkt wspólny.
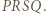 Jest oczywiste, że prosta
Jest oczywiste, że prosta 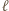 przechodzi przez punkt
przechodzi przez punkt 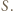 Okrąg opisany na trójkącie
Okrąg opisany na trójkącie 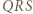 przechodzi przez punkty
przechodzi przez punkty 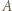 i
i 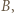 ponadto
ponadto 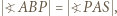 więc prosta
więc prosta 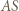 jest styczna do okręgu
jest styczna do okręgu 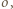 analogicznie prosta
analogicznie prosta 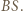 Położenie punktu
Położenie punktu 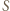 nie zależy zatem od wyboru punktu
nie zależy zatem od wyboru punktu 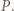
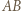 będzie jednym z boków wielokąta środkowosymetrycznego
będzie jednym z boków wielokąta środkowosymetrycznego 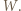 Przez
Przez 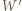 oznaczmy wielokąt
oznaczmy wielokąt 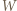 przesunięty o wektor
przesunięty o wektor 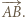 Wówczas wielokąt
Wówczas wielokąt 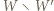 łatwo rozciąć na równoległoboki, a wielokąt
łatwo rozciąć na równoległoboki, a wielokąt 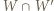 ma środek symetrii i o dwa boki mniej niż wielokąt
ma środek symetrii i o dwa boki mniej niż wielokąt 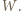
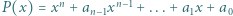 ma
ma  pierwiastków rzeczywistych (licząc z krotnościami). Wiedząc, że
pierwiastków rzeczywistych (licząc z krotnościami). Wiedząc, że 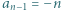 i
i 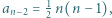 wyznaczyć
wyznaczyć 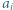 dla
dla 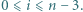
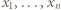 będą pierwiastkami
będą pierwiastkami 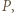 tzn.
tzn. 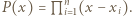 Korzystając ze wzorów Viète'a, mamy
Korzystając ze wzorów Viète'a, mamy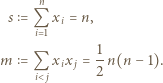
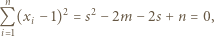
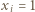 dla
dla 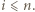 Pozostaje łatwe sprawdzenie, że wielomian
Pozostaje łatwe sprawdzenie, że wielomian 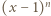 spełnia przedstawione w zadaniu warunki. Dlatego
spełnia przedstawione w zadaniu warunki. Dlatego 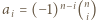 dla
dla 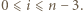
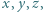 że
że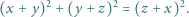
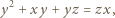
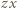 do obu stron daje
do obu stron daje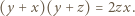
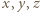 są nieparzyste, to lewa strona powyższej równości jest podzielna przez 4, w przeciwieństwie do prawej strony, co kończy rozwiązanie zadania.
są nieparzyste, to lewa strona powyższej równości jest podzielna przez 4, w przeciwieństwie do prawej strony, co kończy rozwiązanie zadania.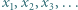 będzie rosnącym ciągiem wszystkich dodatnich liczb
będzie rosnącym ciągiem wszystkich dodatnich liczb 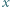 spełniających równanie
spełniających równanie 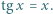 Niech
Niech 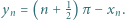 Obliczyć granicę ciągu
Obliczyć granicę ciągu 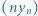 przy
przy 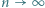 (lub wykazać, że granica nie istnieje).
(lub wykazać, że granica nie istnieje).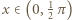 zachodzi nierówność
zachodzi nierówność 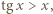 więc w tym przedziale nie leży żaden wyraz ciągu
więc w tym przedziale nie leży żaden wyraz ciągu 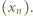 W każdym dalszym przedziale dodatniości funkcji tangens leży jeden wyraz. Tak więc
W każdym dalszym przedziale dodatniości funkcji tangens leży jeden wyraz. Tak więc 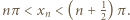 Wobec określenia
Wobec określenia 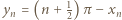 wynika stąd, że
wynika stąd, że 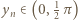 oraz
oraz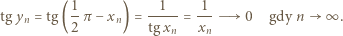
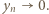 A skoro
A skoro 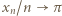 (oraz
(oraz 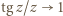 gdy
gdy 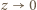 ), zatem
), zatem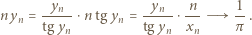
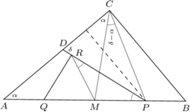
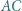 trójkąta prostokątnego
trójkąta prostokątnego 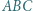 został dowolnie wybrany punkt
został dowolnie wybrany punkt 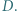 Symetralna odcinka
Symetralna odcinka 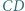 przecina przeciwprostokątną
przecina przeciwprostokątną 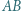 w punkcie
w punkcie 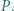 Punkt
Punkt 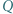 jest symetryczny do
jest symetryczny do 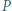 względem środka
względem środka 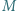 odcinka
odcinka 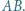 Punkt
Punkt 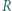 jest rzutem prostokątnym punktu
jest rzutem prostokątnym punktu 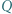 na prostą
na prostą 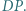 Udowodnić, że
Udowodnić, że 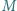 leży na dwusiecznej kąta
leży na dwusiecznej kąta 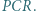
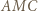 i
i 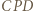 są równoramienne. Przyjmijmy oznaczenia:
są równoramienne. Przyjmijmy oznaczenia: 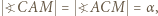
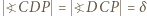 ; zatem
; zatem 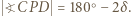 Środek odcinka
Środek odcinka 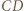 leży bliżej punktu
leży bliżej punktu 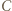 niż punktu
niż punktu 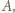 wobec czego punkt
wobec czego punkt 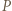 leży między
leży między 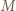 i
i 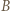 ; w takim razie
; w takim razie 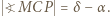 Rachunek kątów w trójkącie
Rachunek kątów w trójkącie 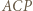 pokazuje, że
pokazuje, że 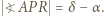
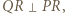 trójkąt
trójkąt 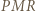 jest równoramienny, więc
jest równoramienny, więc 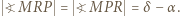 Uzyskujemy równość
Uzyskujemy równość 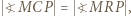 z której wynika, że czworokąt
z której wynika, że czworokąt 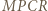 ma okrąg opisany. Skoro
ma okrąg opisany. Skoro 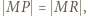 punkt
punkt 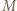 jest środkiem łuku
jest środkiem łuku 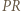 tego okręgu; a to znaczy, że półprosta
tego okręgu; a to znaczy, że półprosta 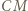 połowi kąt
połowi kąt 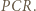 To teza zadania.
To teza zadania.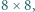 jeden czarne, a drugi białe. Żadne dwa pionki tego samego koloru nie mogą stać na polach mających wspólny bok lub wierzchołek. Przegrywa ten, kto nie może wykonać ruchu. Wskazać strategię wygrywającą.
jeden czarne, a drugi białe. Żadne dwa pionki tego samego koloru nie mogą stać na polach mających wspólny bok lub wierzchołek. Przegrywa ten, kto nie może wykonać ruchu. Wskazać strategię wygrywającą.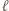 będzie osią symetrii szachownicy, równoległą do pewnych dwóch jej boków. Gracz drugi ma strategię wygrywającą - każdy swój pionek stawia symetrycznie do postawionego w poprzednim ruchu pionka przeciwnika względem prostej
będzie osią symetrii szachownicy, równoległą do pewnych dwóch jej boków. Gracz drugi ma strategię wygrywającą - każdy swój pionek stawia symetrycznie do postawionego w poprzednim ruchu pionka przeciwnika względem prostej 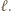
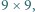 przy czym hetmana można postawić wyłącznie na wolnym polu, którego nie atakuje żaden z hetmanów ustawionych wcześniej. Przegrywa gracz, który nie może wykonać ruchu. Wskazać strategię wygrywającą.
przy czym hetmana można postawić wyłącznie na wolnym polu, którego nie atakuje żaden z hetmanów ustawionych wcześniej. Przegrywa gracz, który nie może wykonać ruchu. Wskazać strategię wygrywającą.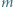 na
na 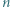 kostek. Dwaj gracze na zmianę łamią czekoladę wzdłuż linii prostej, nie uszkadzając kostek. Po złamaniu czekolady gracz wybiera jeden z dwóch otrzymanych kawałków i zjada go, a gra toczy się dalej na pozostałej części czekolady. Wygrywa ten, kto odda przeciwnikowi ostatnią kostkę. Wskazać strategię wygrywającą.
kostek. Dwaj gracze na zmianę łamią czekoladę wzdłuż linii prostej, nie uszkadzając kostek. Po złamaniu czekolady gracz wybiera jeden z dwóch otrzymanych kawałków i zjada go, a gra toczy się dalej na pozostałej części czekolady. Wygrywa ten, kto odda przeciwnikowi ostatnią kostkę. Wskazać strategię wygrywającą.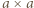 ) można otrzymać tylko z niekwadratowej. Zatem receptą na zwycięstwo jest tworzenie kwadratu, o ile to możliwe. Jeśli
) można otrzymać tylko z niekwadratowej. Zatem receptą na zwycięstwo jest tworzenie kwadratu, o ile to możliwe. Jeśli 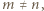 to zwycięży pierwszy gracz, a w przeciwnym razie - drugi.
to zwycięży pierwszy gracz, a w przeciwnym razie - drugi.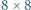 skoczki, przy czym gracz pierwszy stawia zawsze jednego, a gracz drugi trzy. Skoczki muszą stać na różnych polach i żadne dwa nie mogą się atakować. Przegrywa ten, kto nie może wykonać ruchu. Wskazać strategię wygrywającą.
skoczki, przy czym gracz pierwszy stawia zawsze jednego, a gracz drugi trzy. Skoczki muszą stać na różnych polach i żadne dwa nie mogą się atakować. Przegrywa ten, kto nie może wykonać ruchu. Wskazać strategię wygrywającą.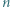 srebrnych i
srebrnych i 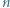 złotych. Ruch polega na zabraniu pewnej liczby monet z jednego lub dwóch stosów, ale złotych monet musi pozostać co najmniej tyle, co srebrnych. Ponadto, jeśli zabieramy monety z obu stosów, to po wykonaniu ruchu muszą one zawierać po tyle samo monet. Wygrywa gracz, który pozostawi na stole jedną złotą monetę i żadnej srebrnej. Wskazać strategię wygrywającą.
złotych. Ruch polega na zabraniu pewnej liczby monet z jednego lub dwóch stosów, ale złotych monet musi pozostać co najmniej tyle, co srebrnych. Ponadto, jeśli zabieramy monety z obu stosów, to po wykonaniu ruchu muszą one zawierać po tyle samo monet. Wygrywa gracz, który pozostawi na stole jedną złotą monetę i żadnej srebrnej. Wskazać strategię wygrywającą.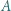 lub
lub 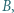 jedną na jeden ruch. Drugi może w swoim ruchu zamienić miejscami dowolne dwie litery napisanego słowa albo może nic nie zmieniać. Gra kończy się, gdy każdy z graczy wykona
jedną na jeden ruch. Drugi może w swoim ruchu zamienić miejscami dowolne dwie litery napisanego słowa albo może nic nie zmieniać. Gra kończy się, gdy każdy z graczy wykona 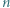 ruchów. Drugi gracz wygrywa, gdy powstałe słowo
ruchów. Drugi gracz wygrywa, gdy powstałe słowo 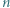 -literowe jest palindromem; w przeciwnym razie wygrywa pierwszy. Wskazać strategię wygrywającą.
-literowe jest palindromem; w przeciwnym razie wygrywa pierwszy. Wskazać strategię wygrywającą.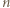 jest liczbą parzystą, to gracz pierwszy wygrywa, pisząc raz literę
jest liczbą parzystą, to gracz pierwszy wygrywa, pisząc raz literę 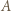 i
i 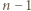 razy literę
razy literę 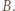 Gdy
Gdy 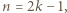 to wygrywa gracz drugi w następujący sposób. Przez pierwszych
to wygrywa gracz drugi w następujący sposób. Przez pierwszych 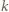 ruchów nie robi nic, a po napisaniu litery
ruchów nie robi nic, a po napisaniu litery 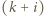 -tej sprawdza, czy jest ona taka sama jak
-tej sprawdza, czy jest ona taka sama jak 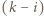 -ta. Jeśli tak, to nic nie robi, a jeśli nie, to literę
-ta. Jeśli tak, to nic nie robi, a jeśli nie, to literę 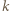 -tą zamienia z tą z liter
-tą zamienia z tą z liter 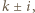 która jest od niej inna.
która jest od niej inna.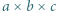 złożony jest z
złożony jest z 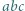 sześcianików o wymiarach
sześcianików o wymiarach 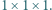 Ruch polega na przebiciu tego prostopadłościanu igłą na wylot, równolegle do wybranej krawędzi. W czasie ruchu zostaje przebitych
Ruch polega na przebiciu tego prostopadłościanu igłą na wylot, równolegle do wybranej krawędzi. W czasie ruchu zostaje przebitych 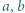 lub
lub  sześcianików. Żaden sześcianik nie może być przebity dwa razy, a przegrywa gracz, który jako pierwszy nie może wbić igły zgodnie z podanymi prawidłami. Wskazać strategię wygrywającą.
sześcianików. Żaden sześcianik nie może być przebity dwa razy, a przegrywa gracz, który jako pierwszy nie może wbić igły zgodnie z podanymi prawidłami. Wskazać strategię wygrywającą.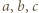 są parzyste, to wygrywa drugi gracz, wykonując ruchy środkowosymetryczne względem środka prostopadłościanu do ruchów gracza pierwszego. Jeśli są co najmniej dwie nieparzyste, powiedzmy
są parzyste, to wygrywa drugi gracz, wykonując ruchy środkowosymetryczne względem środka prostopadłościanu do ruchów gracza pierwszego. Jeśli są co najmniej dwie nieparzyste, powiedzmy 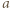 i
i 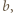 to strategię wygrywającą ma gracz pierwszy. Najpierw wbija igłę w środek ściany
to strategię wygrywającą ma gracz pierwszy. Najpierw wbija igłę w środek ściany 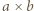 (ta igła przechodzi przez środek prostopadłościanu), a następnie odpowiada środkowosymetrycznie względem środka prostopadłościanu.
(ta igła przechodzi przez środek prostopadłościanu), a następnie odpowiada środkowosymetrycznie względem środka prostopadłościanu.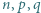 będą liczbami całkowitymi dodatnimi. Ciąg liczb całkowitych
będą liczbami całkowitymi dodatnimi. Ciąg liczb całkowitych 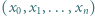 spełnia warunki:
spełnia warunki: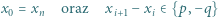
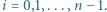 Udowodnić, że jeżeli
Udowodnić, że jeżeli 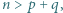 to istnieją takie
to istnieją takie 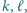 że
że 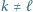 i
i 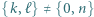 oraz
oraz 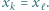
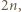 a jego wierzchołkami będą kolejno
a jego wierzchołkami będą kolejno 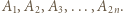 Dla
Dla 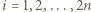 niech
niech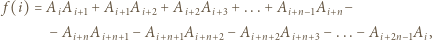
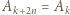 dla
dla 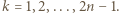 Innymi słowy,
Innymi słowy, 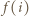 jest różnicą długości części, na które dzielą obwód wielokąta punkty
jest różnicą długości części, na które dzielą obwód wielokąta punkty 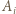 oraz
oraz 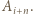 Ponieważ
Ponieważ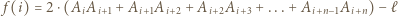
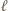 jest obwodem danego wielokąta), to
jest obwodem danego wielokąta), to 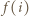 jest liczbą parzystą. Ponadto mamy
jest liczbą parzystą. Ponadto mamy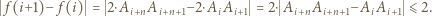
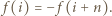 Stąd wynika, że ciąg liczb
Stąd wynika, że ciąg liczb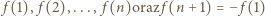
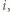 że
że 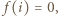 czyli punkty
czyli punkty 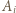 oraz
oraz 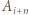 dzielą obwód danego wielokąta na dwie części o jednakowej długości.
dzielą obwód danego wielokąta na dwie części o jednakowej długości.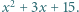 Następnie wszyscy uczniowie w klasie podchodzili kolejno do tablicy; każdy z nich zmniejszał albo zwiększał o jeden współczynnik przy
Następnie wszyscy uczniowie w klasie podchodzili kolejno do tablicy; każdy z nich zmniejszał albo zwiększał o jeden współczynnik przy  albo wyraz wolny trójmianu. Na koniec okazało się, że na tablicy widnieje trójmian
albo wyraz wolny trójmianu. Na koniec okazało się, że na tablicy widnieje trójmian 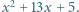 Udowodnić, że w pewnym momencie na tablicy był napisany trójmian o pierwiastkach całkowitych.
Udowodnić, że w pewnym momencie na tablicy był napisany trójmian o pierwiastkach całkowitych.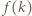 będzie wartością danego trójmianu w punkcie
będzie wartością danego trójmianu w punkcie 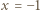 po zmianie współczynników przez
po zmianie współczynników przez 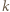 -tego ucznia i niech
-tego ucznia i niech 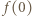 będzie wartością w -1 trójmianu napisanego przez nauczyciela. Zauważmy, że
będzie wartością w -1 trójmianu napisanego przez nauczyciela. Zauważmy, że 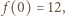 a
a 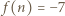 (gdzie
(gdzie 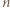 to numer ostatniego ucznia). Ponadto zachodzi nierówność
to numer ostatniego ucznia). Ponadto zachodzi nierówność 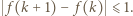 Rzeczywiście - jest to jasne, gdy zmieniamy wyraz wolny, zaś zmieniając o
Rzeczywiście - jest to jasne, gdy zmieniamy wyraz wolny, zaś zmieniając o 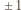 wartość współczynnika przy
wartość współczynnika przy 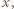 dodajemy lub odejmujemy 1 do wartości wielomianu w -1. W takim razie istnieje takie
dodajemy lub odejmujemy 1 do wartości wielomianu w -1. W takim razie istnieje takie 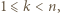 że
że 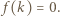 Zatem w pewnym momencie na tablicy był napisany trójmian
Zatem w pewnym momencie na tablicy był napisany trójmian 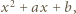 którego jednym z pierwiastków było -1; ze wzorów Viète'a wnosimy, że drugim jego pierwiastkiem była liczba całkowita
którego jednym z pierwiastków było -1; ze wzorów Viète'a wnosimy, że drugim jego pierwiastkiem była liczba całkowita 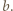
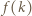 dla
dla 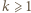 będzie liczbą liczb pierwszych w zbiorze
będzie liczbą liczb pierwszych w zbiorze 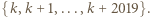 Wśród pierwszych 2020 liczb całkowitych dodatnich jest więcej niż 13 liczb pierwszych, zatem
Wśród pierwszych 2020 liczb całkowitych dodatnich jest więcej niż 13 liczb pierwszych, zatem 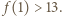 Zauważmy także, że wśród liczb
Zauważmy także, że wśród liczb 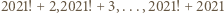 występują same liczby złożone, zatem
występują same liczby złożone, zatem 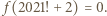 Oczywiście mamy
Oczywiście mamy 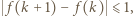 skąd wniosek, że istnieje taka liczba
skąd wniosek, że istnieje taka liczba 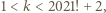 dla której mamy
dla której mamy 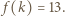 To kończy rozwiązanie zadania.
To kończy rozwiązanie zadania.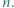 Każdy element zbioru
Każdy element zbioru 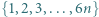 pomalowano na biało albo na czarno, przy czym dokładnie
pomalowano na biało albo na czarno, przy czym dokładnie 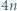 elementów jest białych. Wykazać, że w tym zbiorze istnieje
elementów jest białych. Wykazać, że w tym zbiorze istnieje 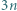 kolejnych liczb całkowitych, wśród których dokładnie
kolejnych liczb całkowitych, wśród których dokładnie 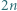 liczb jest białych.
liczb jest białych.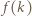 dla
dla 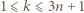 będzie liczbą elementów zbioru
będzie liczbą elementów zbioru 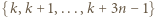 pomalowanych na biało. Zauważmy, że
pomalowanych na biało. Zauważmy, że 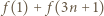 jest liczbą elementów zbioru
jest liczbą elementów zbioru 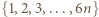 pomalowanych na biało, czyli
pomalowanych na biało, czyli 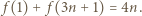 Jeśli
Jeśli 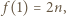 to teza zadania zachodzi. W przeciwnym razie
to teza zadania zachodzi. W przeciwnym razie 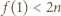 albo
albo 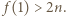 Przyjmijmy bez straty ogólności, że spełniony jest pierwszy przypadek (drugi jest analogiczny). Wtedy
Przyjmijmy bez straty ogólności, że spełniony jest pierwszy przypadek (drugi jest analogiczny). Wtedy 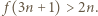 Jest jasne, że
Jest jasne, że 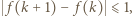 zatem istnieje taka liczba
zatem istnieje taka liczba 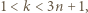 dla której mamy
dla której mamy 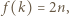 co jest równoważne z tezą zadania.
co jest równoważne z tezą zadania.