Środek przeciwprostokątnej»Zadanie 6
o zadaniu...
- Zadanie pochodzi z artykułu Środek przeciwprostokątnej
- Publikacja w Delcie: sierpień 2017
- Publikacja elektroniczna: 30 lipca 2017
- Artykuł źródłowy w wersji do druku [application/pdf]: (99 KB)
Proste 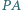 i
i 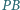 są styczne do okręgu
są styczne do okręgu 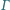 odpowiednio w punktach
odpowiednio w punktach 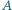 i
i 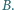 Punkt
Punkt 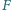 jest rzutem prostokątnym punktu
jest rzutem prostokątnym punktu 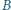 na średnicę
na średnicę 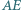 okręgu
okręgu 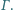 Wykaż, że środek odcinka
Wykaż, że środek odcinka 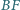 leży na prostej
leży na prostej 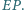

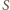 punkt przecięcia prostych
punkt przecięcia prostych 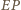 i
i 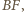 a przez
a przez 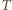 - punkt przecięcia prostych
- punkt przecięcia prostych 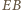 i
i 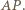 Obydwie proste
Obydwie proste 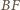 i
i 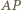 są prostopadłe do
są prostopadłe do 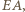 więc trójkąty
więc trójkąty 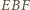 oraz
oraz 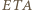 są podobne i
są podobne i 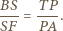
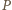 jest środkiem odcinka
jest środkiem odcinka 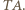
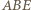 jest prosty (gdyż
jest prosty (gdyż 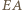 jest średnicą okręgu), stąd także kąt
jest średnicą okręgu), stąd także kąt 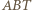 jest prosty. Odcinki
jest prosty. Odcinki 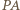 i
i 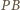 są równe jako styczne do okręgu. Wobec tego punkt
są równe jako styczne do okręgu. Wobec tego punkt 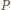 leży na przeciwprostokątnej trójkąta prostokątnego
leży na przeciwprostokątnej trójkąta prostokątnego 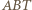 i zarazem na symetralnej jednej z przyprostokątnych, jest więc środkiem okręgu opisanego na tym trójkącie, czyli także środkiem boku
i zarazem na symetralnej jednej z przyprostokątnych, jest więc środkiem okręgu opisanego na tym trójkącie, czyli także środkiem boku 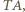 co kończy dowód.
co kończy dowód.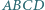 zachodzą równości:
zachodzą równości:
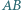 i
i 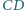 nie przekracza 4.
nie przekracza 4.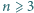 punktów
punktów 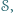 że dla każdego
że dla każdego 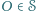 istnieją
istnieją 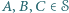 o tej własności, że punkt
o tej własności, że punkt 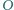 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 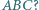
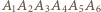 będzie sześciokątem foremnym o boku 1, a
będzie sześciokątem foremnym o boku 1, a 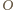 będzie środkiem okręgu opisanego na tym sześciokącie. Wówczas
będzie środkiem okręgu opisanego na tym sześciokącie. Wówczas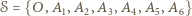
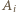 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 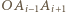 dla
dla 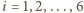 (przyjmujemy
(przyjmujemy 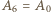 i
i 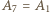 ).
).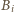 środek okręgu opisanego na trójkącie
środek okręgu opisanego na trójkącie 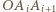 dla
dla 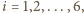 a przez
a przez 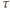 - dowolną translację o wektor długości większej od
- dowolną translację o wektor długości większej od 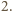 Wówczas, jeżeli
Wówczas, jeżeli 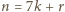 dla
dla 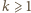 oraz
oraz 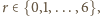 to zbiór
to zbiór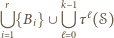
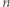 elementów i spełnia warunki zadania (
elementów i spełnia warunki zadania ( 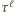 oznacza
oznacza 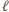 -krotne złożenie
-krotne złożenie  ).
).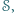 że dla każdych trzech niewspółliniowych punktów
że dla każdych trzech niewspółliniowych punktów 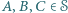 środek okręgu opisanego na trójkącie
środek okręgu opisanego na trójkącie 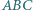 również należy do
również należy do 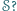
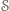 istnieje. Spośród wszystkich odcinków o obu końcach w zbiorze
istnieje. Spośród wszystkich odcinków o obu końcach w zbiorze 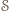 wybierzmy taki, który ma najmniejszą długość i nazwijmy go
wybierzmy taki, który ma najmniejszą długość i nazwijmy go 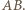 Ponieważ zbiór
Ponieważ zbiór 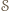 nie jest zawarty w prostej, więc poza prostą
nie jest zawarty w prostej, więc poza prostą 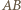 jest co najmniej jeden punkt zbioru
jest co najmniej jeden punkt zbioru 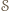 - spośród wszystkich takich punktów wybierzmy taki punkt
- spośród wszystkich takich punktów wybierzmy taki punkt 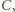 dla którego miara kąta
dla którego miara kąta 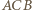 jest największa.
jest największa.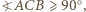 to
to 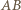 jest najdłuższym bokiem trójkąta
jest najdłuższym bokiem trójkąta 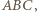 co przeczy wyborowi odcinka
co przeczy wyborowi odcinka 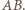 Z kolei jeżeli
Z kolei jeżeli 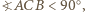 to środek
to środek  okręgu opisanego na trójkącie
okręgu opisanego na trójkącie 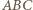 należy do
należy do 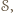 przy czym
przy czym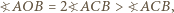
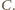 Uzyskana sprzeczność oznacza, że nie istnieje zbiór
Uzyskana sprzeczność oznacza, że nie istnieje zbiór 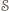 o zadanych własnościach.
o zadanych własnościach.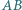 jest najkrótszym bokiem trójkąta
jest najkrótszym bokiem trójkąta 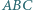 opisanego na okręgu o środku w punkcie
opisanego na okręgu o środku w punkcie 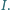 Na bokach
Na bokach 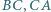 znajdują się odpowiednio takie punkty
znajdują się odpowiednio takie punkty 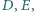 że
że 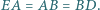 Odcinki
Odcinki 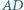 i
i 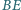 przecinają się w punkcie
przecinają się w punkcie 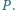 Wykazać, że proste
Wykazać, że proste 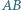 i
i 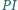 są prostopadłe.
są prostopadłe.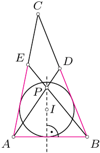
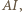 jako dwusieczna kąta między ramionami trójkąta równoramiennego
jako dwusieczna kąta między ramionami trójkąta równoramiennego 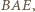 jest prostopadła do podstawy
jest prostopadła do podstawy 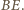 Podobnie prosta
Podobnie prosta 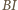 jest prostopadła do prostej
jest prostopadła do prostej 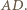 Wobec tego punkt
Wobec tego punkt 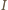 jest ortocentrum trójkąta
jest ortocentrum trójkąta 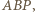 a zatem
a zatem 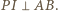
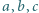 większe od
większe od 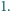 Następnie na kartce zapisano w przypadkowej kolejności cztery liczby, będące wynikami działań
Następnie na kartce zapisano w przypadkowej kolejności cztery liczby, będące wynikami działań 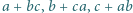 oraz
oraz 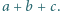 Czy znając liczby napisane na kartce można jednoznacznie określić, jakie trzy liczby znajdują się na tablicy?
Czy znając liczby napisane na kartce można jednoznacznie określić, jakie trzy liczby znajdują się na tablicy?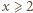 oraz
oraz 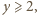 to
to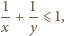
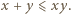 To oznacza, że
To oznacza, że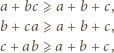
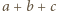 ; oznaczmy tę liczbę przez
; oznaczmy tę liczbę przez 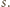 Pozostałe liczby oznaczmy przez
Pozostałe liczby oznaczmy przez 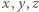 i przyjmijmy (bez straty ogólności, z uwagi na symetrię ról liczb z tablicy), że
i przyjmijmy (bez straty ogólności, z uwagi na symetrię ról liczb z tablicy), że 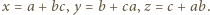 Wówczas
Wówczas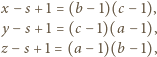
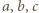 są większe od
są większe od 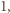 to
to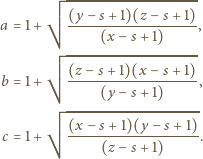
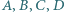 są takimi czterema wierzchołkami pewnego prostopadłościanu, że żadne dwa z nich nie są połączone krawędzią. Sfery
są takimi czterema wierzchołkami pewnego prostopadłościanu, że żadne dwa z nich nie są połączone krawędzią. Sfery 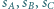 o środkach odpowiednio w punktach
o środkach odpowiednio w punktach 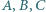 są parami styczne. Udowodnić, że istnieje sfera
są parami styczne. Udowodnić, że istnieje sfera 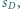 o środku w punkcie
o środku w punkcie 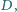 która jest styczna do sfer
która jest styczna do sfer 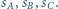
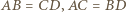 oraz
oraz 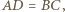 gdyż są to pary przekątnych przystających prostokątów.
gdyż są to pary przekątnych przystających prostokątów.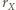 promień sfery
promień sfery 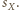 Jeżeli sfery
Jeżeli sfery 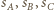 są parami styczne, to pewne dwie z nich - bez straty ogólności
są parami styczne, to pewne dwie z nich - bez straty ogólności 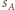 i
i 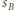 - są styczne zewnętrznie, czyli
- są styczne zewnętrznie, czyli 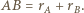 Jeśli
Jeśli 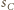 jest styczna zewnętrznie do
jest styczna zewnętrznie do 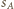 i
i 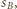 to
to 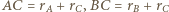 i wystarczy przyjąć
i wystarczy przyjąć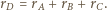
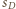 będzie styczna wewnętrznie do pozostałych trzech sfer, gdyż
będzie styczna wewnętrznie do pozostałych trzech sfer, gdyż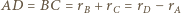

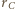 jest styczna wewnętrznie do
jest styczna wewnętrznie do 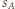 i
i 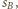 to
to
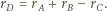
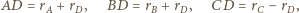
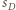 będzie styczna zewnętrznie do
będzie styczna zewnętrznie do 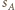 i
i 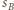 oraz styczna wewnętrznie do
oraz styczna wewnętrznie do 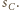
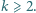 Niech
Niech 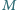 będzie takim zbiorem dodatnich liczb całkowitych, że dla każdej pary różnych liczb
będzie takim zbiorem dodatnich liczb całkowitych, że dla każdej pary różnych liczb 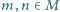 zachodzi nierówność
zachodzi nierówność 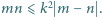 Wykazać, że zbiorze
Wykazać, że zbiorze 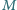 jest nie więcej niż
jest nie więcej niż 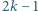 liczb. Czy dla każdej liczby
liczb. Czy dla każdej liczby 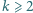 istnieje
istnieje 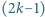 -elementowy zbiór
-elementowy zbiór 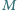 o podanej własności?
o podanej własności?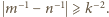 Niech
Niech 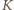 będzie zbiorem odwrotności wszystkich liczb za zbioru
będzie zbiorem odwrotności wszystkich liczb za zbioru 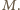 Dowolne dwa elementy zbioru
Dowolne dwa elementy zbioru 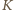 są więc oddalone o co najmniej
są więc oddalone o co najmniej 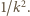 Zatem w każdym spośród
Zatem w każdym spośród 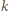 przedziałów
przedziałów![(0, 1-], (-1,-2-], ( 2-,-3] ,...,( k-−1, k-] k2 k2 k2 k2 k2 k2 k2](/math/temat/matematyka/kombinatoryka/zadania/2017/05/29/zm-k44-744/7x-d28462c3f0c14c690f4776454216c605e7515ddb-dm-66,57,43-FF,FF,FF.gif)
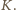 Pozostałe liczby dodatnie tworzą przedział
Pozostałe liczby dodatnie tworzą przedział 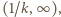 w którym są jedynie odwrotności liczb naturalnych
w którym są jedynie odwrotności liczb naturalnych 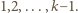 To pokazuje, że zbiór
To pokazuje, że zbiór 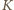 (więc i zbiór
(więc i zbiór 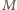 ) może liczyć co najwyżej
) może liczyć co najwyżej 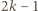 elementów.
elementów.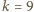 nie istnieje
nie istnieje 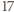 -elementowy zbiór
-elementowy zbiór 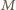 o podanej własności. Jak w przypadku ogólnym, zauważamy, że w każdym z przedziałów
o podanej własności. Jak w przypadku ogólnym, zauważamy, że w każdym z przedziałów ![|(0, 181] ,( 181,821],(821, 381]](/math/temat/matematyka/kombinatoryka/zadania/2017/05/29/zm-k44-744/4x-6cac8931e3035b7a31fa43086bacf339c85f8ab3-im-66,57,43-FF,FF,FF.gif) może być tylko jeden element zbioru
może być tylko jeden element zbioru 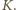 Dalej, odwrotności liczb naturalnych, leżące w przedziale
Dalej, odwrotności liczb naturalnych, leżące w przedziale ![(-1, 1] , 27 9](/math/temat/matematyka/kombinatoryka/zadania/2017/05/29/zm-k44-744/6x-6cac8931e3035b7a31fa43086bacf339c85f8ab3-im-66,57,43-FF,FF,FF.gif) rozbijamy na pięć podzbiorów:
rozbijamy na pięć podzbiorów: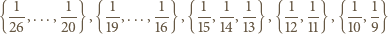
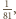 więc zawiera co najwyżej jeden element zbioru
więc zawiera co najwyżej jeden element zbioru 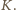 No i zostają jeszcze ułamki
No i zostają jeszcze ułamki 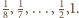 Liczność zbioru
Liczność zbioru 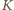 (więc i
(więc i 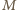 ) nie przekracza
) nie przekracza 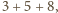 czyli 16.
czyli 16.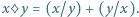 Niech
Niech 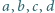 będą liczbami, spełniającymi równanie
będą liczbami, spełniającymi równanie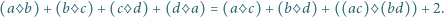
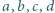 mogą być czterema różnymi liczbami? Czy mogą być wśród nich trzy różne liczby?
mogą być czterema różnymi liczbami? Czy mogą być wśród nich trzy różne liczby?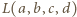 oznacza lewą stronę podanego równania, pomnożoną przez
oznacza lewą stronę podanego równania, pomnożoną przez 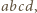 i niech
i niech 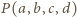 oznacza prawą stronę tego równania, pomnożoną przez
oznacza prawą stronę tego równania, pomnożoną przez 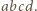 Są to wielomiany czterech zmiennych, jednorodne, czwartego stopnia. Skontrolujmy ich wartości, gdy np.
Są to wielomiany czterech zmiennych, jednorodne, czwartego stopnia. Skontrolujmy ich wartości, gdy np. 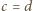 :
: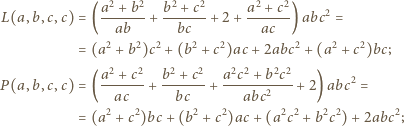
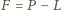 dzieli się przez dwumian
dzieli się przez dwumian 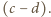 Analogicznie (wobec niezmienniczości przy cyklicznym przesunięciu zmiennych) dzieli się przez dwumiany
Analogicznie (wobec niezmienniczości przy cyklicznym przesunięciu zmiennych) dzieli się przez dwumiany 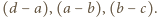 Stąd wniosek, że dzieli się przez iloczyn tych dwumianów, a iloraz jest pewną stałą. Biorąc dowolne różne liczby
Stąd wniosek, że dzieli się przez iloczyn tych dwumianów, a iloraz jest pewną stałą. Biorąc dowolne różne liczby 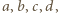 stwierdzamy, że ta stała to 1. Tak więc
stwierdzamy, że ta stała to 1. Tak więc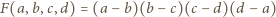
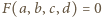 nie jest spełnione dla żadnej czwórki różnych liczb
nie jest spełnione dla żadnej czwórki różnych liczb 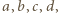 jest zaś spełnione dla wielu czwórek utworzonych z trzech różnych liczb (z jednym powtórzeniem).
jest zaś spełnione dla wielu czwórek utworzonych z trzech różnych liczb (z jednym powtórzeniem).
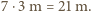 Stąd na mocy twierdzenia Pitagorasa długość winorośli to 29 m.
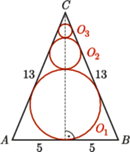
Stąd na mocy twierdzenia Pitagorasa długość winorośli to 29 m.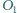 jest wpisany w trójkąt
jest wpisany w trójkąt 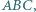 w którym
w którym 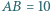 i
i 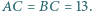 Okręgi
Okręgi 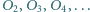 są styczne do boków
są styczne do boków 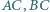 oraz dla każdego
oraz dla każdego 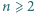 okrąg
okrąg 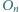 jest styczny zewnętrznie do okręgów
jest styczny zewnętrznie do okręgów 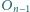 i
i  Wyznacz sumę obwodów wszystkich okręgów
Wyznacz sumę obwodów wszystkich okręgów 
 która z kolei z twierdzenia Pitagorasa ma długość 12. Okrąg o średnicy
która z kolei z twierdzenia Pitagorasa ma długość 12. Okrąg o średnicy 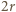 ma obwód
ma obwód 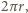 zatem szukana suma obwodów wszystkich okręgów to
zatem szukana suma obwodów wszystkich okręgów to 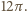
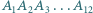 o środku
o środku 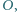 przy czym
przy czym 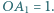 Punkt
Punkt 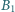 jest rzutem
jest rzutem 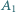 na odcinek
na odcinek 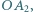 punkt
punkt 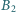 jest rzutem
jest rzutem 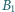 na
na 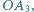 punkt
punkt 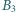 jest rzutem
jest rzutem 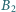 na
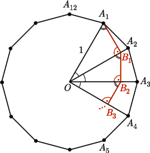
na 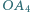 itd. Wyznacz długość łamanej
itd. Wyznacz długość łamanej 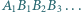

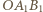 oraz
oraz 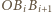 mają kąty po
mają kąty po 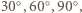 gdyż każdy z nich z założenia jest prostokątny i ma kąt
gdyż każdy z nich z założenia jest prostokątny i ma kąt 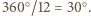 Można wobec tego ułożyć je w sposób przedstawiony na rysunku. Kąt pomiędzy sąsiadującymi teraz odcinkami rozważanej łamanej jest wówczas równy
Można wobec tego ułożyć je w sposób przedstawiony na rysunku. Kąt pomiędzy sąsiadującymi teraz odcinkami rozważanej łamanej jest wówczas równy 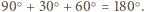
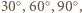 przy czym jedna jego przyprostokątna ma długość 1, a suma pozostałych dwóch boków to szukana długość łamanej. Jest ona wobec tego równa
przy czym jedna jego przyprostokątna ma długość 1, a suma pozostałych dwóch boków to szukana długość łamanej. Jest ona wobec tego równa 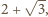 gdyż trójkąt ten jest połową trójkąta równobocznego o boku 2.
gdyż trójkąt ten jest połową trójkąta równobocznego o boku 2.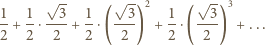
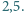 Wykaż, że obwód tego czworokąta jest większy od 7.
Wykaż, że obwód tego czworokąta jest większy od 7.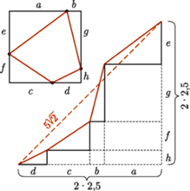
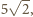 co z kolei jest większe od 7.
co z kolei jest większe od 7.
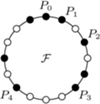
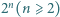 znajdują się punkty
znajdują się punkty 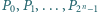 będące wierzchołkami
będące wierzchołkami 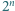 -kąta foremnego, oznaczone w taki sposób, że długość łuku
-kąta foremnego, oznaczone w taki sposób, że długość łuku 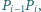 mierzonego zgodnie z ruchem wskazówek zegara, jest równa
mierzonego zgodnie z ruchem wskazówek zegara, jest równa 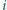 dla każdego
dla każdego 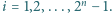 Niech
Niech
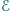 i
i 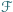 są przystające (jako podzbiory płaszczyzny).
są przystające (jako podzbiory płaszczyzny).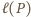 będzie długością łuku (mierzoną zgodnie z ruchem wskazówek zegara) łączącego
będzie długością łuku (mierzoną zgodnie z ruchem wskazówek zegara) łączącego 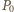 z
z 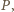 tzn. dla każdego
tzn. dla każdego 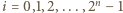
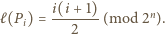
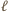 jest bijekcją zbioru wierzchołków
jest bijekcją zbioru wierzchołków 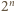 -kąta i
-kąta i ![|Z ∩ [0,2n −1].](/math/temat/matematyka/geometria/planimetria/zadania/2017/04/30/zm-1530/8x-5a02d8212f68e6296da2e894dc2a3a250bf72f4c-im-66,57,43-FF,FF,FF.gif)
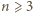 zachodzi równość
zachodzi równość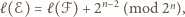
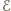 jest obrazem
jest obrazem 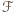 przy obrocie o
przy obrocie o 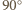 wokół środka danego okręgu zgodnie z ruchem wskazówek zegara. Konkretnie, wykażemy, że dla każdego
wokół środka danego okręgu zgodnie z ruchem wskazówek zegara. Konkretnie, wykażemy, że dla każdego 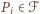
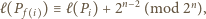
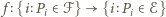 określona jest następująco
określona jest następująco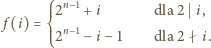
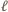 wystarczy więc sprawdzić, że dla każdego
wystarczy więc sprawdzić, że dla każdego 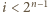 liczba
liczba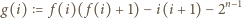
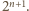 Rzeczywiście, bezpośrednio z definicji funkcji
Rzeczywiście, bezpośrednio z definicji funkcji 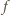 otrzymujemy, że jeżeli
otrzymujemy, że jeżeli 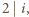 to
to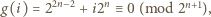
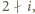 to
to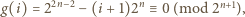
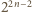 dzieli się przez
dzieli się przez 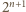 dla
dla 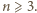 Pozostaje bezpośrednio sprawdzić, że dla
Pozostaje bezpośrednio sprawdzić, że dla 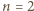 rozważane zbiory także są przystające (odpowiednia izometria znów jest obrotem o
rozważane zbiory także są przystające (odpowiednia izometria znów jest obrotem o 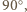 ale w przeciwną stronę).
ale w przeciwną stronę).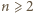 istnieje etykietowanie wierzchołków
istnieje etykietowanie wierzchołków 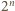 -kąta foremnego o opisanych własnościach - jest to równoważne zadaniu 2 z I etapu LX OM, którego rozwiązanie można znaleźć na stronie
-kąta foremnego o opisanych własnościach - jest to równoważne zadaniu 2 z I etapu LX OM, którego rozwiązanie można znaleźć na stronie  z zaznaczonymi zbiorami
z zaznaczonymi zbiorami  oraz
oraz 
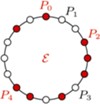
 oraz
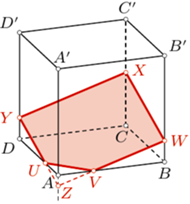
oraz  w taki sposób, aby odcinki
w taki sposób, aby odcinki 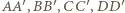 były krawędziami sześcianu oraz ściana
były krawędziami sześcianu oraz ściana 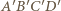 nie zawierała żadnego z boków uzyskanego w przekroju pięciokąta, a krawędź
nie zawierała żadnego z boków uzyskanego w przekroju pięciokąta, a krawędź 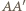 - żadnego z jego wierzchołków. Niech ponadto
- żadnego z jego wierzchołków. Niech ponadto 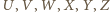 będą punktami przecięcia płaszczyzny przekroju odpowiednio z prostymi
będą punktami przecięcia płaszczyzny przekroju odpowiednio z prostymi 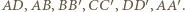
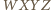 jest równoległobokiem, co wynika z równoległości przeciwległych ścian sześcianu. Okrąg wpisany w pięciokąt
jest równoległobokiem, co wynika z równoległości przeciwległych ścian sześcianu. Okrąg wpisany w pięciokąt 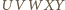 jest wpisany w ten równoległobok, skąd wniosek, że
jest wpisany w ten równoległobok, skąd wniosek, że 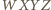 jest rombem. Wykażemy, że
jest rombem. Wykażemy, że 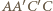 jest płaszczyzną symetrii tego rombu; ponieważ jest to także płaszczyzna symetrii wyjściowego sześcianu, więc wyniknie stąd, że punkty
jest płaszczyzną symetrii tego rombu; ponieważ jest to także płaszczyzna symetrii wyjściowego sześcianu, więc wyniknie stąd, że punkty 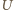 i
i 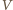 są względem niej symetryczne, co zakończy rozwiązanie.
są względem niej symetryczne, co zakończy rozwiązanie.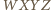 jest rombem, to ma prostopadłe przekątne, a zatem punkty
jest rombem, to ma prostopadłe przekątne, a zatem punkty 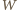 oraz
oraz 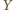 są zawarte w płaszczyźnie symetralnej odcinka
są zawarte w płaszczyźnie symetralnej odcinka 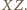 Płaszczyzna ta nie pokrywa się z płaszczyzną
Płaszczyzna ta nie pokrywa się z płaszczyzną 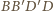 (punkt
(punkt 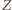 nie należy do odcinka
nie należy do odcinka 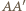 ), więc przecina się z nią wzdłuż prostej prostopadłej do płaszczyzny
), więc przecina się z nią wzdłuż prostej prostopadłej do płaszczyzny 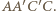 Wobec tego punkty
Wobec tego punkty 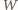 i
i 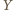 są symetryczne względem płaszczyzny
są symetryczne względem płaszczyzny 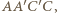 a to właśnie należało udowodnić.
a to właśnie należało udowodnić.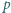 będzie liczbą pierwszą postaci
będzie liczbą pierwszą postaci 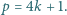 Dowieść, że istnieje liczba całkowita dodatnia
Dowieść, że istnieje liczba całkowita dodatnia 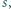 mniejsza od
mniejsza od 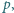 dla której różnica
dla której różnica 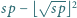 jest kwadratem liczby całkowitej dodatniej.
jest kwadratem liczby całkowitej dodatniej.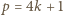 jest sumą dwóch kwadratów (jedno z dobrze znanych twierdzeń Fermata):
jest sumą dwóch kwadratów (jedno z dobrze znanych twierdzeń Fermata): 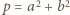 ; liczby całkowite
; liczby całkowite 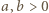 muszą być względnie pierwsze. Istnieją wobec tego liczby całkowite
muszą być względnie pierwsze. Istnieją wobec tego liczby całkowite 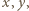 dla których
dla których 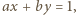 przy czym
przy czym 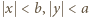 (łatwe uzasadnienie przez algorytm Euklidesa).
(łatwe uzasadnienie przez algorytm Euklidesa).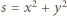 ma własności, o które chodzi w zadaniu. Mamy bowiem oszacowanie
ma własności, o które chodzi w zadaniu. Mamy bowiem oszacowanie 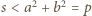 oraz równość
oraz równość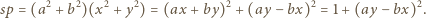
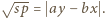 W konsekwencji
W konsekwencji 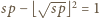 ; jest to niewątpliwie kwadrat liczby całkowitej dodatniej.
; jest to niewątpliwie kwadrat liczby całkowitej dodatniej.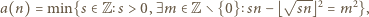
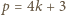 zachodzi równość
zachodzi równość 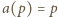 ; natomiast dla liczb pierwszych
; natomiast dla liczb pierwszych 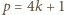 zachodzi nierówność
zachodzi nierówność 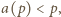 i to była treść naszego zadania; autorem podanego dowodu jest Robert Israel. (Dla liczb złożonych ciąg zachowuje się dość kapryśnie).
i to była treść naszego zadania; autorem podanego dowodu jest Robert Israel. (Dla liczb złożonych ciąg zachowuje się dość kapryśnie).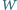 będzie wielościanem wypukłym, środkowo-symetrycznym, i niech
będzie wielościanem wypukłym, środkowo-symetrycznym, i niech 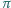 będzie ustaloną płaszczyzną, przechodzącą przez środek symetrii. Przekrój wielościanu
będzie ustaloną płaszczyzną, przechodzącą przez środek symetrii. Przekrój wielościanu 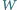 płaszczyzną
płaszczyzną 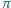 jest zawarty w kole o promieniu
jest zawarty w kole o promieniu 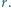 Udowodnić, że przekrój wielościanu
Udowodnić, że przekrój wielościanu 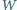 każdą płaszczyzną, równoległą do
każdą płaszczyzną, równoległą do 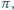 jest zawarty w pewnym kole o promieniu
jest zawarty w pewnym kole o promieniu  - lub podać przykład, pokazujący nieprawdziwość takiego stwierdzenia.
- lub podać przykład, pokazujący nieprawdziwość takiego stwierdzenia.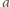 ). Weźmy jego dwa przeciwległe wierzchołki
). Weźmy jego dwa przeciwległe wierzchołki 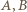 (końce przekątnej długości
(końce przekątnej długości 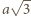 ). Płaszczyzna
). Płaszczyzna 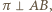 przechodząca przez środek
przechodząca przez środek 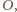 tworzy w przecięciu z sześcianem sześciokąt foremny, którego wierzchołkami są środki niektórych krawędzi sześcianu, leżące w odległości
tworzy w przecięciu z sześcianem sześciokąt foremny, którego wierzchołkami są środki niektórych krawędzi sześcianu, leżące w odległości 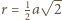 od środka
od środka 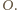
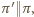 przechodzącą przez trzy wierzchołki (połączone krawędziami np. z punktem
przechodzącą przez trzy wierzchołki (połączone krawędziami np. z punktem 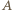 ) jest trójkątem foremnym o boku
) jest trójkątem foremnym o boku 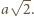 Najmniejsze koło, zawierające ów trójkąt, ma promień
Najmniejsze koło, zawierające ów trójkąt, ma promień