Wykłady popularne z matematyki»Zadanie 5
o zadaniu...
- Zadanie pochodzi z artykułu Wykłady popularne z matematyki
- Publikacja w Delcie: maj 2011
- Publikacja elektroniczna: 04-05-2011
Na balu spotkało się
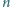 pań i
pań i
 panów, niektórzy są
zaznajomieni. Jakie warunki muszą być spełnione, by mogli dobrać się
do tańca w pary, w których się znają?
panów, niektórzy są
zaznajomieni. Jakie warunki muszą być spełnione, by mogli dobrać się
do tańca w pary, w których się znają?
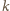 panów musi znać łącznie co najmniej
panów musi znać łącznie co najmniej
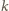 pań.
pań.
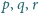 takie, że liczba
takie, że liczba

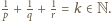 Pomnóżmy obie strony
równania przez
Pomnóżmy obie strony
równania przez
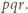 Wtedy
Wtedy
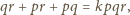
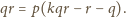
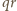 dzieli się przez
dzieli się przez
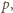 sprzeczność. Zatem liczby
sprzeczność. Zatem liczby
 o żądanych własnościach nie istnieją.
o żądanych własnościach nie istnieją.
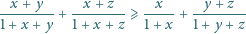
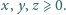
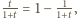 nierówność dana do udowodnienia jest
równoważna następującej:
nierówność dana do udowodnienia jest
równoważna następującej:
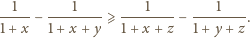
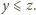
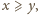 to w ostatniej nierówności lewa strona jest
nieujemna, prawa jest niedodatnia i nie ma czego dowodzić.
to w ostatniej nierówności lewa strona jest
nieujemna, prawa jest niedodatnia i nie ma czego dowodzić.
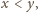 możemy tak przekształcać lewą stronę i szacować ją
z dołu, by uzyskać wyrażenie widoczne po prawej stronie:
możemy tak przekształcać lewą stronę i szacować ją
z dołu, by uzyskać wyrażenie widoczne po prawej stronie:
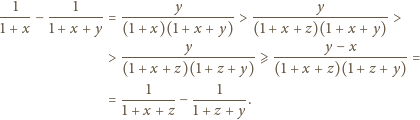
 i
i
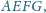 tak samo zorientowane, mają wspólny
tylko punkt
tak samo zorientowane, mają wspólny
tylko punkt
 Wykaż, że
Wykaż, że
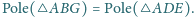
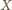 będzie czwartym wierzchołkiem równoległoboku
będzie czwartym wierzchołkiem równoległoboku
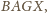 a
a
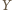 – czwartym wierzchołkiem równoległoboku
– czwartym wierzchołkiem równoległoboku
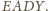 Równoległoboki te są przystające, ponieważ
Równoległoboki te są przystające, ponieważ
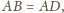
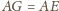 oraz
oraz
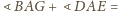
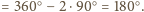 Stąd
Stąd
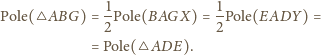
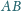 i
i
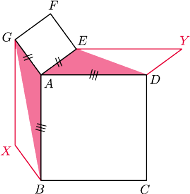
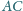 trójkąta
trójkąta
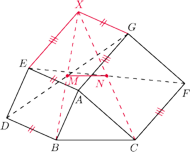
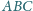 zbudowano, po jego
zewnętrznej stronie, kwadraty
zbudowano, po jego
zewnętrznej stronie, kwadraty
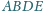 i
i
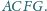 Punkty
Punkty
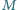 i
i
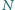 są odpowiednio środkami odcinków
są odpowiednio środkami odcinków
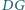 i
i
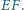 Wyznacz możliwe wartości wyrażenia
Wyznacz możliwe wartości wyrażenia
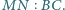
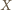 będzie czwartym wierzchołkiem równoległoboku
będzie czwartym wierzchołkiem równoległoboku
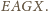 Wtedy
Wtedy
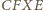 także jest równoległobokiem (bo
także jest równoległobokiem (bo
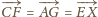 ). Wobec tego punkt
). Wobec tego punkt
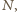 jako środek jego przekątnej
jako środek jego przekątnej
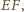 jest też środkiem drugiej przekątnej
jest też środkiem drugiej przekątnej
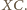 Analogicznie
Analogicznie
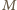 jest środkiem
jest środkiem
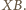 Stąd i z twierdzenia Talesa uzyskujemy
Stąd i z twierdzenia Talesa uzyskujemy
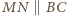 oraz
oraz
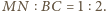
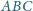 zachodzi równość
zachodzi równość
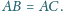 Punkt
Punkt
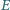 jest środkiem wysokości
jest środkiem wysokości
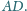 Punkt
Punkt
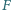 jest rzutem
prostokątnym punktu
jest rzutem
prostokątnym punktu
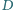 na prostą
na prostą
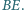 Udowodnij, że
Udowodnij, że
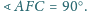
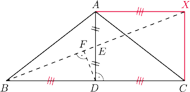
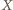 będzie czwartym wierzchołkiem prostokąta
będzie czwartym wierzchołkiem prostokąta
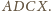 Wtedy
Wtedy
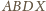 jest równoległobokiem o środku
jest równoległobokiem o środku
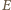 (bo
(bo
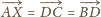 oraz
oraz
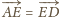 ), więc punkty
), więc punkty
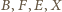 są
współliniowe. Odcinki
są
współliniowe. Odcinki
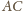 i
i
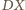 są średnicami okręgu opisanego
na prostokącie
są średnicami okręgu opisanego
na prostokącie
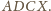 Ponadto
Ponadto
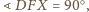 więc punkt
więc punkt
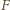 leży na tym okręgu. Stąd
leży na tym okręgu. Stąd
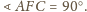
 leży wewnątrz równoległoboku
leży wewnątrz równoległoboku
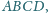 przy czym
przy czym
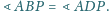 Wykaż, że
Wykaż, że
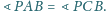
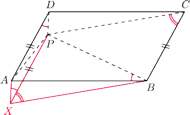
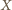 będzie czwartym wierzchołkiem równoległoboku
będzie czwartym wierzchołkiem równoległoboku
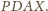 Wtedy
Wtedy
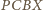 także jest równoległobokiem oraz
zachodzą równości
także jest równoległobokiem oraz
zachodzą równości
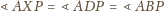
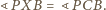
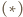 (uwzględniając wzajemne położenie odpowiednich
punktów) wynika, że punkty
(uwzględniając wzajemne położenie odpowiednich
punktów) wynika, że punkty
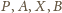 leżą na jednym okręgu. Wobec
tego
leżą na jednym okręgu. Wobec
tego
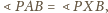 co razem z równością
co razem z równością
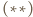 daje tezę.
daje tezę.
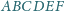 o polu 1 przeciwległe boki są
równe i równoległe. Wyznacz pole trójkąta
o polu 1 przeciwległe boki są
równe i równoległe. Wyznacz pole trójkąta
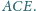
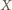 będzie czwartym wierzchołkiem równoległoboku
będzie czwartym wierzchołkiem równoległoboku
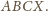 Wtedy
Wtedy
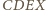 i
i
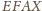 też są równoległobokami...
też są równoległobokami...
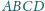 punkty
punkty
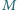 i
i
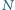 są środkami odpowiednio
ramion
są środkami odpowiednio
ramion
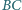 i
i
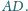 Wykaż, że
Wykaż, że
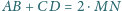 i że
i że


 Wykaż, że z jego środkowych można
zbudować trójkąt.
Wykaż, że z jego środkowych można
zbudować trójkąt.
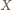 będzie czwartym wierzchołkiem równoległoboku
będzie czwartym wierzchołkiem równoległoboku
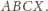
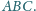 Punkty
Punkty
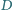 i
i
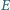 należą odpowiednio do boków
należą odpowiednio do boków
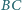 i
i
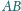 tego
trójkąta i
tego
trójkąta i
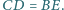 Punkt
Punkt
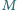 jest środkiem odcinka
jest środkiem odcinka
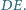 Udowodnij, że
Udowodnij, że
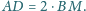
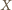 będzie czwartym wierzchołkiem równoległoboku
będzie czwartym wierzchołkiem równoległoboku
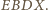
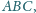 w którym
w którym
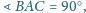 jest podstawą
ostrosłupa
jest podstawą
ostrosłupa
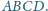 Ponadto zachodzą równości
Ponadto zachodzą równości
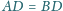 oraz
oraz
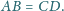 Wykaż, że
Wykaż, że
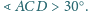
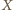 będzie czwartym wierzchołkiem prostokąta
będzie czwartym wierzchołkiem prostokąta
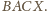
 zapisano jako
zapisano jako
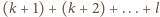 dla
pewnych liczb naturalnych
dla
pewnych liczb naturalnych
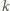 i
i
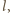 takich że
takich że
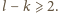 To
oznacza, że
To
oznacza, że
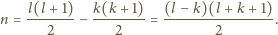
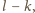
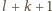 jest nieparzysta
i większa od
jest nieparzysta
i większa od
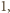 czyli
czyli
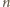 ma czynnik nieparzysty, więc nie jest potęgą
dwójki. Z drugiej strony, jeżeli
ma czynnik nieparzysty, więc nie jest potęgą
dwójki. Z drugiej strony, jeżeli
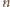 nie jest potęgą dwójki, to
liczba
nie jest potęgą dwójki, to
liczba
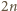 zapisuje się jako iloczyn liczby parzystej i nieparzystej
zapisuje się jako iloczyn liczby parzystej i nieparzystej
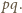 Jeśli
Jeśli
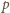 oznacza większą z tych liczb, to możemy przyjąć,
iż
oznacza większą z tych liczb, to możemy przyjąć,
iż
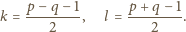
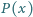 będzie wielomianem stopnia dodatniego o współczynnikach
całkowitych. Wykazać, że dla każdej liczby naturalnej
będzie wielomianem stopnia dodatniego o współczynnikach
całkowitych. Wykazać, że dla każdej liczby naturalnej
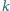 istnieje taka
liczba całkowita
istnieje taka
liczba całkowita
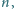 że liczba
że liczba
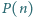 ma co najmniej
ma co najmniej
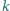 różnych dzielników pierwszych.
różnych dzielników pierwszych.
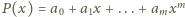 (
(
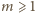 ).
).
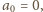 wystarczy wziąć dowolną liczbę
wystarczy wziąć dowolną liczbę
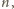 będącą iloczynem
będącą iloczynem
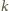 różnych liczb pierwszych. Są one oczywiście dzielnikami liczby
różnych liczb pierwszych. Są one oczywiście dzielnikami liczby
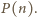 Dalej przyjmijmy, że
Dalej przyjmijmy, że
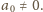
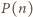 jest nieskończony. Przypuśćmy bowiem, że jest to zbiór
skończony
jest nieskończony. Przypuśćmy bowiem, że jest to zbiór
skończony
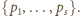 Biorąc jako
Biorąc jako
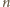 dowolną liczbę postaci
dowolną liczbę postaci
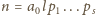 (
(
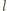 całkowite), mamy
całkowite), mamy
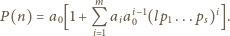
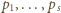 (a swoboda wyboru
(a swoboda wyboru
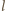 pozwala przyjąć, że jest różna
od
pozwala przyjąć, że jest różna
od
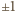 ); ma więc jakiś inny dzielnik pierwszy, wbrew uczynionemu
przypuszczeniu.
); ma więc jakiś inny dzielnik pierwszy, wbrew uczynionemu
przypuszczeniu.
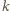 istnieją różne liczby pierwsze
istnieją różne liczby pierwsze
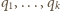 oraz takie liczby całkowite
oraz takie liczby całkowite
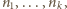 że
że
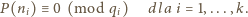
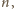 spełniającą układ kongruencji
spełniającą układ kongruencji

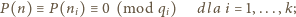
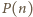 ma więc co najmniej
ma więc co najmniej
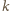 różnych dzielników
pierwszych.
różnych dzielników
pierwszych.
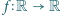 jest dana wzorem
jest dana wzorem
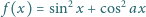
 ). Dowieść, że jeżeli
). Dowieść, że jeżeli
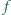 jest
funkcją okresową, to
jest
funkcją okresową, to
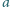 jest liczbą wymierną.
jest liczbą wymierną.
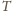 będzie okresem funkcji
będzie okresem funkcji
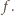 Z równości
Z równości
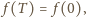 czyli
czyli
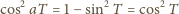
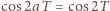 ) wnosimy, że
) wnosimy, że
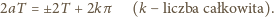
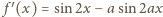 też jest funkcją
też jest funkcją
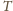 -okresową:
-okresową:
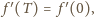 czyli
czyli
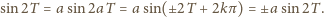
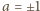 (liczba wymierna), albo
(liczba wymierna), albo
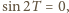 skąd
skąd
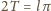 (
(
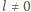 ),
),
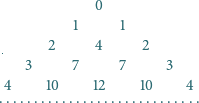
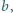
 są sąsiednimi elementami
dowolnego wiersza, nad nimi znajduje się liczba
są sąsiednimi elementami
dowolnego wiersza, nad nimi znajduje się liczba
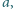 zaś pod nimi liczba
zaś pod nimi liczba
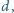 to
to
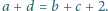 Udowodnić, że dla każdej liczby
całkowitej
Udowodnić, że dla każdej liczby
całkowitej
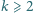 istnieje nieskończenie wiele liczb, z których każda
występuje w tej tabeli dokładnie
istnieje nieskończenie wiele liczb, z których każda
występuje w tej tabeli dokładnie
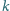 razy.
razy.
 tak, by otrzymać tabelę – nieskończoną
macierz
tak, by otrzymać tabelę – nieskończoną
macierz
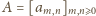 ; jest to lewa z dwóch tabelek poniżej:
; jest to lewa z dwóch tabelek poniżej:

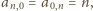
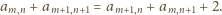
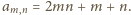 Sprawdzamy, że te liczby spełniają
napisane przed chwilą równania (które wyznaczają zawartość całej tabeli
jednoznacznie).
Sprawdzamy, że te liczby spełniają
napisane przed chwilą równania (które wyznaczają zawartość całej tabeli
jednoznacznie).
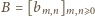 o wyrazach
o wyrazach
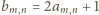 (prawy diagram powyżej). Zachodzą równości
(prawy diagram powyżej). Zachodzą równości
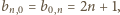
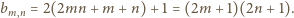
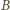 jest po prostu tabliczką mnożenia liczb nieparzystych. Każda
liczba nieparzysta występuje w niej tyle razy, ile ma różnych dzielników
dodatnich.
jest po prostu tabliczką mnożenia liczb nieparzystych. Każda
liczba nieparzysta występuje w niej tyle razy, ile ma różnych dzielników
dodatnich.
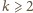 będzie zadaną liczbą całkowitą. Bierzemy dowolną
liczbę pierwszą
będzie zadaną liczbą całkowitą. Bierzemy dowolną
liczbę pierwszą
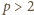 ; wówczas liczba
; wówczas liczba
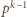 wystąpi w tabeli
wystąpi w tabeli
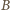 dokładnie
dokładnie
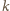 razy. Wracając do tabeli
razy. Wracając do tabeli
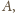 widzimy, że
dokładnie
widzimy, że
dokładnie
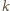 razy pojawi się w niej liczba
razy pojawi się w niej liczba
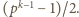 Jest
nieskończenie wiele liczb pierwszych – mamy więc tezę zadania.
Jest
nieskończenie wiele liczb pierwszych – mamy więc tezę zadania.
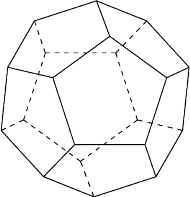
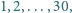 używając każdej z nich dokładnie raz.
Rozstrzygnij, czy można to uczynić, tak aby suma numerów krawędzi
wychodzących z dowolnego wierzchołka była:
używając każdej z nich dokładnie raz.
Rozstrzygnij, czy można to uczynić, tak aby suma numerów krawędzi
wychodzących z dowolnego wierzchołka była:
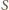 oznacza sumę wszystkich numerów
krawędzi:
oznacza sumę wszystkich numerów
krawędzi:
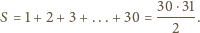
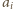 oznacza sumę numerów w
oznacza sumę numerów w
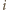 -tym wierzchołku (
-tym wierzchołku (
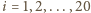 ). Wtedy
). Wtedy
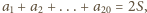 bo numer każdej
krawędzi jest liczony dwukrotnie – przy każdym z jej końców. Gdyby
każda z liczb
bo numer każdej
krawędzi jest liczony dwukrotnie – przy każdym z jej końców. Gdyby
każda z liczb
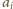 była podzielna przez 4, to
była podzielna przez 4, to
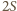 także. Jednak
także. Jednak
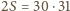 nie dzieli się przez 4.
nie dzieli się przez 4.
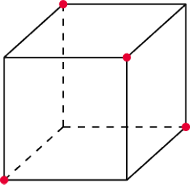
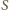 oznacza ich sumę, a
oznacza ich sumę, a
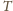 – sumę pozostałych czterech liczb.
Opisana operacja nie zmienia
– sumę pozostałych czterech liczb.
Opisana operacja nie zmienia
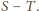 Początkowo
Początkowo
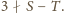 Tymczasem gdyby
Tymczasem gdyby
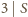 i
i
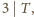 to
to
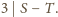
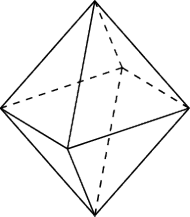
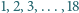 można rozstawić w wierzchołkach
i na środkach krawędzi ośmiościanu foremnego, tak aby każda
liczba na krawędzi ośmiościanu była średnią arytmetyczną liczb na jej
końcach.
można rozstawić w wierzchołkach
i na środkach krawędzi ośmiościanu foremnego, tak aby każda
liczba na krawędzi ośmiościanu była średnią arytmetyczną liczb na jej
końcach.