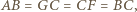Panaceum?»Zadanie 1
Rys. 1a
Rys. 1a
Proszę ocenić poprawność poniższego stwierdzenia.
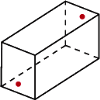
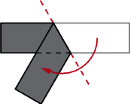
Pokój ma kształt prostopadłościanu o wymiarach 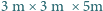 (Rys. 1a). Nad środkiem jednej z krótszych krawędzi podłogi, na wysokości
(Rys. 1a). Nad środkiem jednej z krótszych krawędzi podłogi, na wysokości 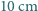 , siedzi pająk. Chce on dotrzeć do punktu położonego
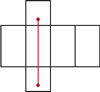
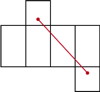
, siedzi pająk. Chce on dotrzeć do punktu położonego 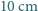 pod przeciwległą krawędzią sufitu. Najkrótszą drogę, o długości 8 m, oznaczono kolorowym odcinkiem na siatce przedstawionej na rysunku 1b.
pod przeciwległą krawędzią sufitu. Najkrótszą drogę, o długości 8 m, oznaczono kolorowym odcinkiem na siatce przedstawionej na rysunku 1b.

 W wierzchołku
W wierzchołku  podstawy siedzi pająk. Chce on przejść po powierzchni bocznej, odwiedzając wszystkie krawędzie boczne (być może w ich końcach) i wrócić do punktu wyjścia. Z rysunku i z nierówności trójkąta wynika, że istnieje droga krótsza niż
podstawy siedzi pająk. Chce on przejść po powierzchni bocznej, odwiedzając wszystkie krawędzie boczne (być może w ich końcach) i wrócić do punktu wyjścia. Z rysunku i z nierówności trójkąta wynika, że istnieje droga krótsza niż 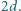

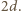
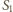 z
z 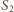 sklejają się w innym punkcie, niż
sklejają się w innym punkcie, niż  z
z  Wynika to z faktu, że na rysunku wysokości trójkątów, poprowadzone z wierzchołków
Wynika to z faktu, że na rysunku wysokości trójkątów, poprowadzone z wierzchołków 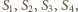 nie przecinają się w jednym punkcie - spodku wysokości ostrosłupa - a powinny.
nie przecinają się w jednym punkcie - spodku wysokości ostrosłupa - a powinny.
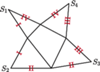
 o wszystkich bokach równej długości i kątach przy wierzchołkach
o wszystkich bokach równej długości i kątach przy wierzchołkach  równych odpowiednio:
równych odpowiednio: 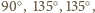
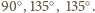 Niech
Niech  będzie punktem przecięcia przekątnych
będzie punktem przecięcia przekątnych  oraz
oraz 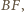 a
a 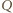 punktem przecięcia przekątnych
punktem przecięcia przekątnych 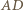 oraz
oraz 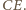 (
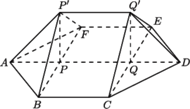
(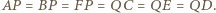 Wybierzmy teraz w przestrzeni punkty
Wybierzmy teraz w przestrzeni punkty 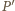 oraz
oraz 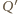 po tej samej stronie płaszczyzny sześciokąta, tak aby proste
po tej samej stronie płaszczyzny sześciokąta, tak aby proste 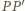 i
i 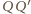 były prostopadłe do tej płaszczyzny oraz aby
były prostopadłe do tej płaszczyzny oraz aby 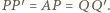 Wielościan
Wielościan 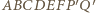 (
(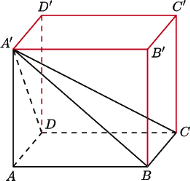
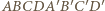 będzie prostopadłościanem. Wówczas ostrosłup
będzie prostopadłościanem. Wówczas ostrosłup 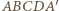 spełnia warunki zadania.
spełnia warunki zadania.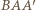 oraz
oraz 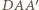 są, oczywiście, prostokątne. Ponadto, ponieważ prosta
są, oczywiście, prostokątne. Ponadto, ponieważ prosta 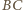 jest prostopadła do płaszczyzny
jest prostopadła do płaszczyzny 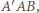 to jest ona prostopadła do każdej prostej z tej płaszczyzny, w szczególności do prostej
to jest ona prostopadła do każdej prostej z tej płaszczyzny, w szczególności do prostej 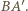 Zatem trójkąt
Zatem trójkąt 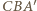 jest prostokątny. Podobnie dowodzimy, że trójkąt
jest prostokątny. Podobnie dowodzimy, że trójkąt  jest prostokątny.
jest prostokątny.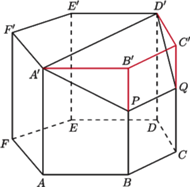
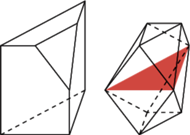
 oraz
oraz  Graniastosłup ten ma 18 krawędzi i wszystkie jego ściany mają parzystą liczbę boków. Gdyby udało się dodać jedną krawędź, nie zmieniając własności ścian, to otrzymany wielościan spełniałby warunki zadania. Zauważmy, że sześciokąt
Graniastosłup ten ma 18 krawędzi i wszystkie jego ściany mają parzystą liczbę boków. Gdyby udało się dodać jedną krawędź, nie zmieniając własności ścian, to otrzymany wielościan spełniałby warunki zadania. Zauważmy, że sześciokąt 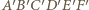 można bez trudu podzielić jedną z przekątnych na dwa czworokąty. Teraz tylko trzeba zrobić z tych czworokątów ściany wielościanu przez pochylenie jednego z nich. Poprowadźmy więc przez punkty
można bez trudu podzielić jedną z przekątnych na dwa czworokąty. Teraz tylko trzeba zrobić z tych czworokątów ściany wielościanu przez pochylenie jednego z nich. Poprowadźmy więc przez punkty 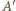 oraz
oraz 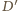 płaszczyznę przecinającą krawędzie
płaszczyznę przecinającą krawędzie 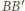 i
i 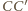 odpowiednio w punktach
odpowiednio w punktach 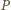 oraz
oraz 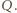 Płaszczyzna ta dzieli graniastosłup na dwa wielościany, z których jeden spełnia warunki zadania: ma osiem ścian będących czworokątami i jedną ścianę sześciokątną. Ponadto wielościan ten ma
Płaszczyzna ta dzieli graniastosłup na dwa wielościany, z których jeden spełnia warunki zadania: ma osiem ścian będących czworokątami i jedną ścianę sześciokątną. Ponadto wielościan ten ma 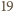 krawędzi.
krawędzi.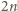 -kątem, dla
-kątem, dla 
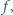 odwzorowująca zbiór liczb całkowitych dodatnich w siebie, jest niemalejąca i spełnia równość
odwzorowująca zbiór liczb całkowitych dodatnich w siebie, jest niemalejąca i spełnia równość 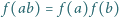 dla dowolnych liczb względnie pierwszych
dla dowolnych liczb względnie pierwszych 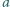 i
i 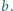 Udowodnić, że
Udowodnić, że
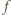 wynika prawdziwość dwóch nierówności:
wynika prawdziwość dwóch nierówności: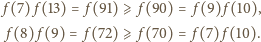
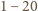 ] wykazał, że funkcja
] wykazał, że funkcja  spełniająca podane warunki musi być postaci
spełniająca podane warunki musi być postaci 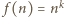 dla pewnego
dla pewnego 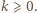
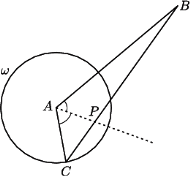
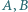 oraz okrąg
oraz okrąg 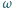 o środku w punkcie
o środku w punkcie 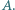 Dla punktu
Dla punktu 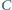 należącego do okręgu
należącego do okręgu 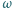 i nienależącego do prostej
i nienależącego do prostej 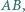 punkt
punkt 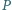 jest przecięciem prostej
jest przecięciem prostej 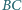 i dwusiecznej kąta
i dwusiecznej kąta 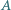 w trójkącie
w trójkącie 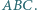 Wyznaczyć zbiór wszystkich otrzymanych w ten sposób punktów
Wyznaczyć zbiór wszystkich otrzymanych w ten sposób punktów 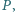 gdy
gdy 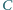 przebiega okrąg
przebiega okrąg 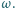

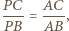 a skąd
a skąd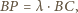
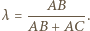
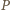 to obraz punktu
to obraz punktu 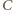 przy jednokładności o środku
przy jednokładności o środku 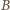 i skali
i skali 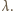 Poszukiwany zbiór punktów
Poszukiwany zbiór punktów 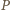 jest więc obrazem okręgu
jest więc obrazem okręgu 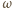 (bez dwóch punktów) przy tej jednokładności.
(bez dwóch punktów) przy tej jednokładności.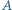 oraz najmniejszą liczbę
oraz najmniejszą liczbę 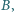 takie że dla każdej czwórki liczb rzeczywistych
takie że dla każdej czwórki liczb rzeczywistych 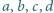 spełniona jest nierówność
spełniona jest nierówność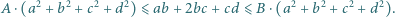
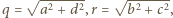
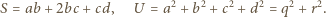
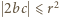 oraz
oraz 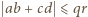 (nier. Cauchy'ego-Schwarza), zatem
(nier. Cauchy'ego-Schwarza), zatem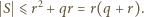
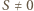 (więc
(więc 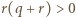 ). Wówczas
). Wówczas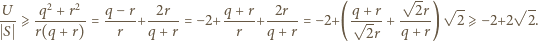
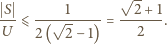
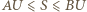 zachodzi ze stałymi
zachodzi ze stałymi 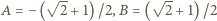 (dla
(dla 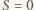 oczywiście też).
oczywiście też).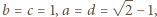 uzyskujemy równość
uzyskujemy równość 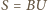 (z podaną stałą
(z podaną stałą 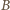 ); zaś zmieniając znak w
); zaś zmieniając znak w  i
i 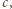 dostajemy równość
dostajemy równość 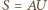 (z podaną stałą
(z podaną stałą 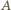 ). Znalezione stałe są więc optymalne.
). Znalezione stałe są więc optymalne. w którym kąty wewnętrzne przy wierzchołkach
w którym kąty wewnętrzne przy wierzchołkach 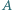 oraz
oraz 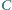 są równe, przy tym ostre. Punkty
są równe, przy tym ostre. Punkty 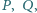 leżące odpowiednio na półprostych
leżące odpowiednio na półprostych 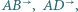 są wyznaczone przez warunki
są wyznaczone przez warunki 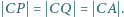 Wykazać, że długość odcinka
Wykazać, że długość odcinka  nie przekracza obwodu trójkąta
nie przekracza obwodu trójkąta 
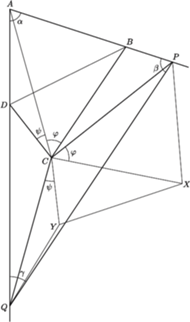
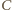 leży wewnątrz trójkąta
leży wewnątrz trójkąta 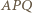 (jest to bowiem środek okręgu opisanego na tym trójkącie, leżący w obrębie kąta ostrego
(jest to bowiem środek okręgu opisanego na tym trójkącie, leżący w obrębie kąta ostrego 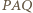 ). Oznaczmy kąty tego trójkąta:
). Oznaczmy kąty tego trójkąta: 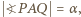
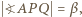
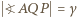 ; ponadto niech
; ponadto niech 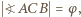
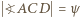 ; z założenia
; z założenia 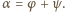
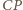 i
i  czworokąta (wklęsłego)
czworokąta (wklęsłego) 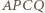 budujemy, po zewnętrznej jego stronie, trójkąty
budujemy, po zewnętrznej jego stronie, trójkąty 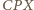 i
i 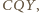 przystające odpowiednio do trójkątów
przystające odpowiednio do trójkątów 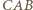 i
i 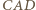 :
: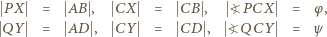
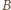 leży między
leży między 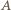 i
i 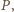 zaś
zaś 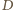 między
między 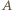 i
i 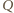 ; ale przy innym uporządkowaniu punktów, na jednej lub drugiej z tych prostych, rozumowanie nie wymaga żadnych zmian). Skoro
; ale przy innym uporządkowaniu punktów, na jednej lub drugiej z tych prostych, rozumowanie nie wymaga żadnych zmian). Skoro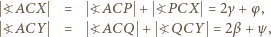
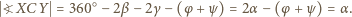
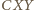 jest przystający do trójkąta
jest przystający do trójkąta 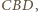 wobec czego
wobec czego 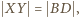 i otrzymujemy tezę zadania:
i otrzymujemy tezę zadania: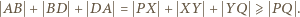

 ma środek w środku kwadratu i jest styczne zewnętrznie do każdego z pozostałych kół (
ma środek w środku kwadratu i jest styczne zewnętrznie do każdego z pozostałych kół (
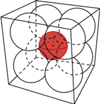
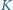 dla sześcianu o krawędzi 2 i ośmiu kul o średnicy 1 (
dla sześcianu o krawędzi 2 i ośmiu kul o średnicy 1 ( -wymiarowej kuli
-wymiarowej kuli 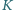 dla
dla  -wymiarowego hipersześcianu o krawędzi 2 i
-wymiarowego hipersześcianu o krawędzi 2 i 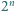 kul
kul 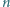 -wymiarowych o średnicy 1.
-wymiarowych o średnicy 1.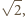 stąd
stąd 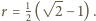
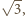 stąd
stąd 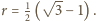
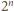 kul równa jest 1, a przekątna hipersześcianu jednostkowego ma długość
kul równa jest 1, a przekątna hipersześcianu jednostkowego ma długość 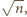 stąd
stąd 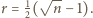
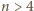 uzyskujemy
uzyskujemy 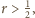 więc "mała" kulka
więc "mała" kulka 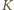 jest większa od każdej z "dużych" kul, a dla
jest większa od każdej z "dużych" kul, a dla 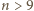 mamy
mamy 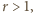 czyli kula
czyli kula 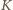 wystaje poza hipersześcian!
wystaje poza hipersześcian!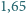 m. Czy istnieje możliwość przesłania fletu?
m. Czy istnieje możliwość przesłania fletu?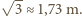


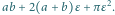

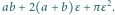
 -otoczkę pudełka o wymiarach
-otoczkę pudełka o wymiarach 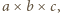 czyli zbiór złożony z wszystkich punktów z jego wnętrza oraz punktów odległych od niego o mniej niż
czyli zbiór złożony z wszystkich punktów z jego wnętrza oraz punktów odległych od niego o mniej niż 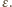 Ma ona kształt większego prostopadłościanu o zaokrąglonych krawędziach i rogach. Jej objętość równa jest
Ma ona kształt większego prostopadłościanu o zaokrąglonych krawędziach i rogach. Jej objętość równa jest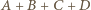
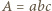 (objętość wyjściowego prostopadłościanu),
(objętość wyjściowego prostopadłościanu),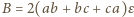 (objętości prostopadłościanów zbudowanych na ścianach),
(objętości prostopadłościanów zbudowanych na ścianach),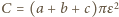 (fragmenty na równoległych krawędziach sumują się do walców o promieniu podstawy
(fragmenty na równoległych krawędziach sumują się do walców o promieniu podstawy  ),
),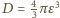 (fragmenty na rogach prostopadłościanu sumują się do kuli o promieniu
(fragmenty na rogach prostopadłościanu sumują się do kuli o promieniu  ).
).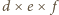 da się włożyć do pudełka o wymiarach
da się włożyć do pudełka o wymiarach 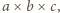 to również
to również  -otoczka pierwszego mieści się w
-otoczka pierwszego mieści się w  -otoczce drugiego. To z kolei oznacza, że różnica objętości jest nieujemna:
-otoczce drugiego. To z kolei oznacza, że różnica objętości jest nieujemna: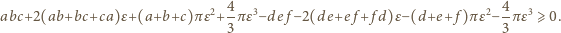
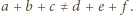
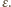 Skoro ma on wartość nieujemną dla każdego
Skoro ma on wartość nieujemną dla każdego 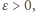 to musi mieć dodatni współczynnik przy najwyższej potędze
to musi mieć dodatni współczynnik przy najwyższej potędze 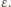 Stąd
Stąd 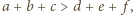 co kończy dowód.
co kończy dowód.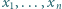 będą liczbami rzeczywistymi dodatnimi, przy czym
będą liczbami rzeczywistymi dodatnimi, przy czym 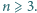 Dla wygody przyjmijmy dodatkowo, że
Dla wygody przyjmijmy dodatkowo, że 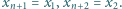
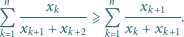
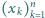 jest monotoniczny, to
jest monotoniczny, to
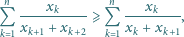
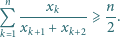
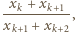 dla
dla 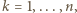 wynosi
wynosi 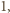 to korzystając z nierówności między średnimi, dostajemy
to korzystając z nierówności między średnimi, dostajemy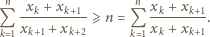
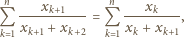
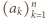 i
i 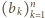 spełniają
spełniają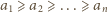
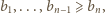
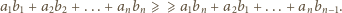
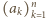 i
i 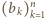 spełniają
spełniają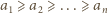
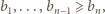
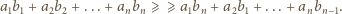
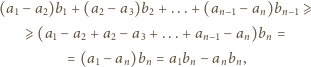
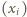 jest nierosnący:
jest nierosnący: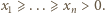
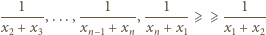
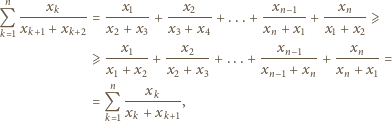
 jest niemalejący, postępujemy analogicznie.
jest niemalejący, postępujemy analogicznie.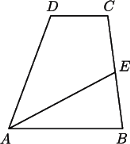
 boki
boki  i
i  są równoległe oraz
są równoległe oraz 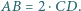 Punkt
Punkt 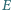 jest środkiem boku
jest środkiem boku 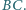 Udowodnić, że jeśli w czworokąt
Udowodnić, że jeśli w czworokąt 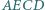 można wpisać okrąg, to
można wpisać okrąg, to 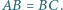
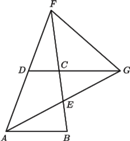
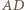 i
i 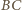 przecinają się w punkcie
przecinają się w punkcie 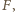 a proste
a proste 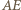 i
i 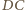 w punkcie
w punkcie 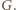
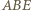 i
i 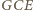 są przystające, a w szczególności
są przystające, a w szczególności 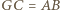 oraz
oraz 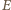 jest środkiem
jest środkiem 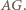 Ponadto
Ponadto 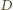 jest środkiem
jest środkiem 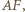 ponieważ odcinek
ponieważ odcinek 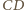 jest równoległy do
jest równoległy do 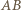 i dwa razy krótszy. Zatem
i dwa razy krótszy. Zatem 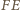 i
i 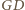 są środkowymi w trójkącie
są środkowymi w trójkącie 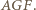
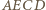 można wpisać okrąg, to zachodzi równość
można wpisać okrąg, to zachodzi równość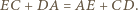
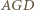 i
i 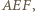 które mają równe pola (równe połowie pola trójkąta
które mają równe pola (równe połowie pola trójkąta 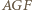 ). W takim razie mają również równe obwody, czyli
). W takim razie mają również równe obwody, czyli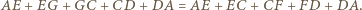
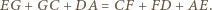
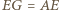 i
i 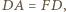 to mamy też
to mamy też 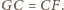 Stąd dostajemy
Stąd dostajemy