Klub 44M - zadania IV 2012»Zadanie 639
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania IV 2012
- Publikacja w Delcie: kwiecień 2012
- Publikacja elektroniczna: 1 kwietnia 2012
- Artykuł źródłowy w wersji do druku [application/pdf]: (78 KB)
W trójkącie
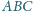 punkt
punkt
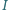 jest środkiem okręgu wpisanego.
Prosta
jest środkiem okręgu wpisanego.
Prosta
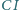 przecina bok
przecina bok
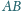 w punkcie
w punkcie
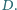 Prowadzimy
przez punkt
Prowadzimy
przez punkt
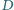 dowolną prostą, przecinającą okrąg opisany na
trójkącie
dowolną prostą, przecinającą okrąg opisany na
trójkącie
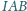 w punktach
w punktach
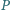 i
i
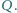 Wykazać, że prosta
Wykazać, że prosta
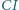 jest dwusieczną kąta
jest dwusieczną kąta
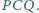

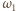 i
i
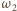 będą (odpowiednio) okręgami opisanymi
na trójkątach
będą (odpowiednio) okręgami opisanymi
na trójkątach
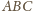 i
i
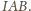 Dwusieczna
Dwusieczna
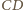 kąta
kąta
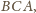 a raczej jej przedłużenie, przecina okrąg
a raczej jej przedłużenie, przecina okrąg
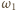 w środku
łuku
w środku
łuku
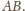 Oznaczmy ten punkt przez
Oznaczmy ten punkt przez
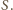 Zachodzi równość
Zachodzi równość
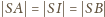 (znana, a przy tym łatwa do wykazania). Punkt
(znana, a przy tym łatwa do wykazania). Punkt
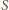 jest więc środkiem okręgu
jest więc środkiem okręgu
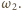 Zatem
Zatem
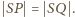
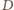 przecinają się cięciwy
przecinają się cięciwy
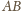 i
i
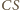 okręgu
okręgu
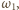 a także cięciwy
a także cięciwy
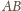 i
i
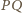 okręgu
okręgu
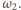 Tak
więc
Tak
więc
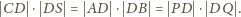
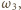 przechodzący przez punkty
przechodzący przez punkty
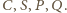 Jego cięciwy
Jego cięciwy
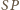 i
i
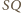 mają jednakową długość, więc wyznaczają przystające
łuki
mają jednakową długość, więc wyznaczają przystające
łuki
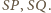 Oparte na nich kąty
Oparte na nich kąty
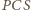 i
i
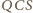 (wpisane
w okrąg
(wpisane
w okrąg
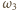 ) są równe – a to jest teza zadania.
) są równe – a to jest teza zadania.

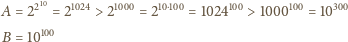
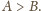
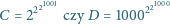
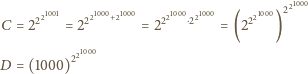
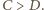

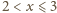 mamy
mamy
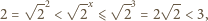
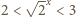 i dalej
i dalej
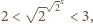 skąd dochodzimy do
skąd dochodzimy do
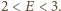
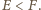

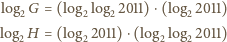
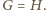

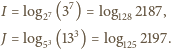
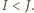
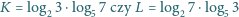
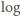 oznacza logarytm przy naszej ulubionej podstawie.
oznacza logarytm przy naszej ulubionej podstawie.
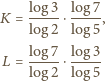
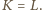
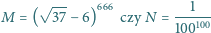
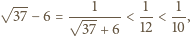
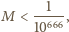
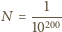
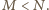

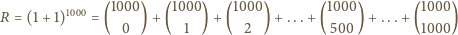
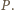
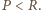
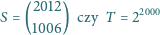
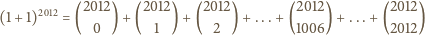
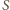 .
.
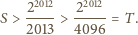
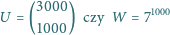
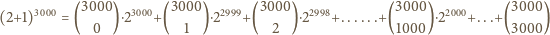
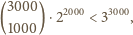
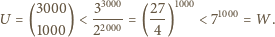
 o współczynnikach całkowitych, dla którego
istnieją takie parami różne liczby całkowite
o współczynnikach całkowitych, dla którego
istnieją takie parami różne liczby całkowite
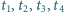 , że
, że

 , dla której
, dla której
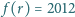 .
.
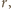 dla
której
dla
której
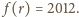 Korzystając z tego, że
Korzystając z tego, że
 dzieli
dzieli
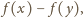 dla dowolnych liczb całkowitych
dla dowolnych liczb całkowitych
 i
i
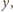 mamy
mamy

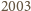 jest pierwsza, więc skoro liczby
jest pierwsza, więc skoro liczby
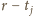 są parami różne,
to bez straty ogólności możemy przyjąć, że
są parami różne,
to bez straty ogólności możemy przyjąć, że

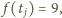 więc po podzieleniu z resztą wielomianu
więc po podzieleniu z resztą wielomianu
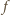 przez wielomian
przez wielomian
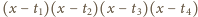 mamy
mamy
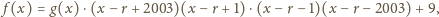
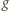 o współczynnikach całkowitych.
Podstawiając
o współczynnikach całkowitych.
Podstawiając
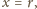 dostajemy
dostajemy
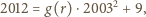
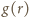 jest liczbą całkowitą.
jest liczbą całkowitą.

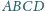 jest styczny do boków
jest styczny do boków
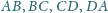 odpowiednio w punktach
odpowiednio w punktach
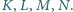 Udowodnij,
że proste
Udowodnij,
że proste
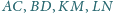 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
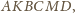 proste
proste
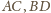 i
i
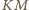 przecinają się
w jednym punkcie. Z kolei z twierdzenia Brianchona dla zdegenerowanego
sześciokąta
przecinają się
w jednym punkcie. Z kolei z twierdzenia Brianchona dla zdegenerowanego
sześciokąta
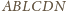 wynika, że przez punkt przecięcia prostych
wynika, że przez punkt przecięcia prostych
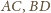 przechodzi także prosta
przechodzi także prosta
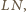 co kończy dowód.
co kończy dowód.
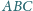 jest styczny do boków
jest styczny do boków
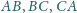 odpowiednio w punktach
odpowiednio w punktach
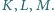 Wykaż, że
proste
Wykaż, że
proste
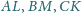 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
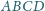 jest opisany na okręgu o środku
jest opisany na okręgu o środku
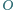 i promieniu 1.
Przekątne tego trapezu przecinają się w punkcie
i promieniu 1.
Przekątne tego trapezu przecinają się w punkcie
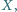 przy czym
przy czym
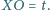 Wyznacz stosunek
Wyznacz stosunek
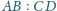 długości podstaw tego
trapezu, jeśli
długości podstaw tego
trapezu, jeśli
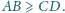
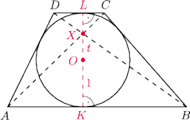
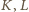 odpowiednio punkty styczności podstaw
odpowiednio punkty styczności podstaw
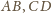 z okręgiem. Wtedy
z okręgiem. Wtedy
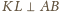 oraz
oraz
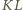 przechodzi
przez punkt
przechodzi
przez punkt
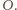 Z twierdzenia Brianchona dla czworokąta,
Z twierdzenia Brianchona dla czworokąta,
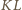 przechodzi też przez punkt
przechodzi też przez punkt
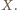 Trójkąty
Trójkąty
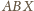 i
i
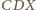 są podobne, więc
są podobne, więc
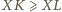 oraz
oraz
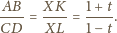
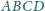 jest styczny do boku
jest styczny do boku
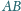 w punkcie
w punkcie
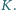 Styczna do tego okręgu przecina boki
Styczna do tego okręgu przecina boki
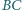 i
i
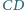 odpowiednio
w punktach
odpowiednio
w punktach
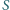 i
i
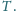 Wykaż, że
Wykaż, że

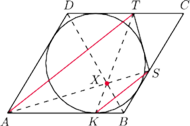
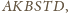 proste
proste
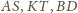 przecinają się w jednym punkcie
przecinają się w jednym punkcie
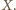 Z twierdzenia
Talesa ponieważ
Z twierdzenia
Talesa ponieważ
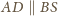 oraz
oraz
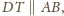 więc
więc
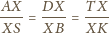
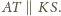
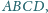 w którym zachodzi równość
w którym zachodzi równość

 jest środkiem okręgu opisanego na trójkacie
jest środkiem okręgu opisanego na trójkacie
 Wykaż, że punkt
Wykaż, że punkt
 jest jednakowo odległy od prostych
jest jednakowo odległy od prostych
 i
i
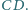
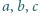 spełniają warunek
spełniają warunek
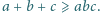 Udowodnić,
że co najwyżej jedna z liczb
Udowodnić,
że co najwyżej jedna z liczb
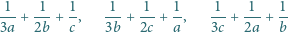
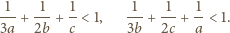
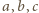 odpowiednio przez
odpowiednio przez
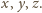 Warunek
Warunek
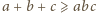 przybiera postać
przybiera postać
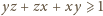 ; zaś dwie domniemane nierówności przepisujemy
jako
; zaś dwie domniemane nierówności przepisujemy
jako
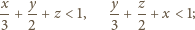

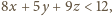 czyli
czyli
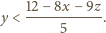
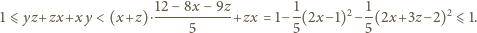
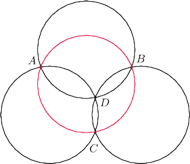
 mają dokładnie jeden punkt
wspólny
mają dokładnie jeden punkt
wspólny
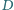 i przecinają się parami jeszcze w punktach
i przecinają się parami jeszcze w punktach
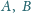 i
i
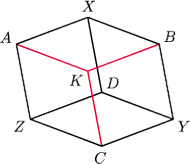
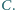 Udowodnić, że okrąg wyznaczony przez punkty
Udowodnić, że okrąg wyznaczony przez punkty
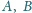 i
i
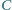 również ma promień długości
również ma promień długości
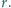
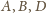 ;
;
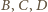 ;
;
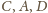 odpowiednio przez
odpowiednio przez
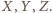 Niech
Niech
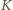 będzie takim punktem, że
będzie takim punktem, że
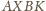 jest rombem. Zauważmy,
że czworokąty
jest rombem. Zauważmy,
że czworokąty
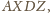
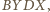
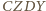 są rombami
o boku długości
są rombami
o boku długości
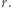 Wobec tego
Wobec tego
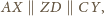 a z definicji
punktu
a z definicji
punktu
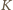 zachodzi
zachodzi
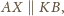 więc
więc
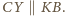 Ponieważ
są to odcinki długości
Ponieważ
są to odcinki długości
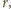 to także
to także
 jest rombem
o boku długości
jest rombem
o boku długości
 Zatem
Zatem
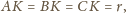 czyli punkty
czyli punkty
 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie
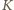 i promieniu
i promieniu
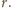
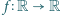 ma cykl długości
ma cykl długości
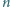 o początku
o początku
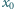 , gdy istnieje takie
, gdy istnieje takie
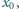 że liczby
że liczby
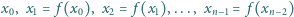 są parami różne, zaś
są parami różne, zaś
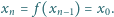
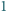 lub
lub
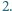
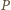 o współczynnikach
całkowitych ma cykl
o współczynnikach
całkowitych ma cykl
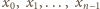 długości
długości
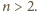 Mamy
Mamy
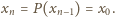 Kluczowa będzie dla nas obserwacja, że dla
dowolnych liczb całkowitych
Kluczowa będzie dla nas obserwacja, że dla
dowolnych liczb całkowitych
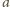 i
i
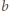 zachodzi
zachodzi
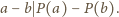
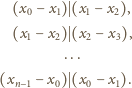
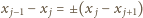
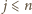 (przyjmujemy, że
(przyjmujemy, że
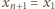 ). Znak „–” jest
wykluczony, gdyż liczby
). Znak „–” jest
wykluczony, gdyż liczby
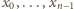 są parami różne. Mamy więc
są parami różne. Mamy więc
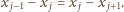 Oznacza to, że ciąg
Oznacza to, że ciąg
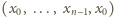 jest
arytmetyczny. Musi on być stały, co daje sprzeczność.
jest
arytmetyczny. Musi on być stały, co daje sprzeczność.