Zadanie ZM-14.11-zadania-1
o zadaniu...
- Publikacja w Delcie: listopad 2014
- Publikacja elektroniczna: 31-10-2014
Wyznacz najmniejszą wartość funkcji kwadratowej 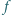 danej wzorem
danej wzorem 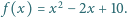
Wyznacz najmniejszą wartość funkcji kwadratowej 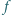 danej wzorem
danej wzorem 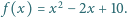
Rozwiąż równanie 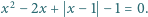
Dane są takie liczby rzeczywiste 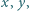 że
że 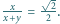 Oblicz
Oblicz 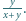
Niech 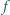 będzie wielomianem o współczynnikach całkowitych o stopniu co najmniej 1. Wykaż, że jeśli
będzie wielomianem o współczynnikach całkowitych o stopniu co najmniej 1. Wykaż, że jeśli  i
i 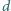 są różnymi liczbami całkowitymi, to
są różnymi liczbami całkowitymi, to  dzieli
dzieli 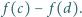
Zbadaj, czy istnieje taki wielomian 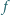 stopnia 3 o współczynnikach całkowitych, że
stopnia 3 o współczynnikach całkowitych, że 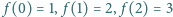 oraz
oraz 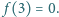
Niech 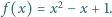 Znajdź wszystkie wartości
Znajdź wszystkie wartości 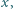 dla których
dla których 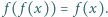
Zadanie 688 zaproponował pan Witold Bednarek z Łodzi.
Trójkąt równoboczny 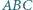 o boku długości 1 jest podstawą ostrosłupa prawidłowego
o boku długości 1 jest podstawą ostrosłupa prawidłowego 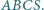 Na krawędziach
Na krawędziach 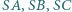 leżą takie punkty
leżą takie punkty 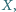
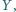
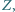 że suma kwadratów pól trójkątów
że suma kwadratów pól trójkątów  jest równa kwadratowi pola trójkąta
jest równa kwadratowi pola trójkąta 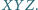 Obliczyć objętość ostrosłupa
Obliczyć objętość ostrosłupa 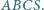
Dowieść, że wśród dowolnie wybranych 39 kolejnych liczb naturalnych znajdzie się liczba, której suma cyfr dzieli się przez 11.
Czy istnieje taki ostrosłup czworokątny, że dwie jego ściany boczne nie mające wspólnej krawędzi są prostopadłe do podstawy?
Wszystkie ściany boczne pewnego ostrosłupa o podstawie kwadratowej są trójkątami równoramiennymi. Czy ostrosłup ten musi być prawidłowy?
Czy istnieje czworościan, którego każda ściana jest trójkątem rozwartokątnym?
Czy wysokości czworościanu muszą przecinać się w jednym punkcie?
Czy istnieje wielościan wypukły, w którym można tak wybrać ponad połowę jego ścian, aby żadne dwie z wybranych ścian nie miały wspólnej krawędzi?
Czy każdy wielościan można striangulować, czyli podzielić na czworościany o wierzchołkach w wierzchołkach wyjściowego wielościanu?
Czy istnieje taki czworościan, w którym spodek żadnej wysokości nie należy do odpowiadającej jej podstawy?
Czy istnieje ostrosłup o podstawie będącej czworokątem wklęsłym, którego dwie ściany boczne nie mające wspólnej krawędzi są prostopadłe do podstawy?
Czy istnieje taki ostrosłup czworokątny oraz taka płaszczyzna przecinająca wszystkie jego krawędzie boczne, że pole uzyskanego przekroju jest większe od pola podstawy ostrosłupa?
Określmy funkcję 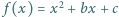 dla pewnych liczb rzeczywistych
dla pewnych liczb rzeczywistych 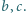 Wiadomo, że zbiór
Wiadomo, że zbiór 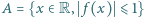 jest zbiorem pustym, odcinkiem lub sumą dwóch odcinków (w zależności od wartości
jest zbiorem pustym, odcinkiem lub sumą dwóch odcinków (w zależności od wartości 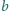 i
i  ). Udowodnić, że za każdym razem łączna długość nie przekracza
). Udowodnić, że za każdym razem łączna długość nie przekracza 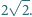
Zadanie 686 zaproponował pan Paweł Kubit z Krakowa
Udowodnić, że istnieje nieskończenie wiele liczb naturalnych 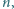 dla których równanie
dla których równanie 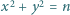 nie ma rozwiązań w liczbach całkowitych
nie ma rozwiązań w liczbach całkowitych 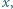
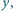 różnych od zera, ale ma rozwiązania w liczbach wymiernych
różnych od zera, ale ma rozwiązania w liczbach wymiernych 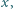
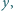 różnych od zera.
różnych od zera.