Rozważane wyrażenie oznaczmy literą 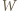 (stale zakładamy, że wszystkie mianowniki są dodatnie). Dwukrotnie stosujemy nierówność między średnimi (po drodze przegrupowując czynniki):
(stale zakładamy, że wszystkie mianowniki są dodatnie). Dwukrotnie stosujemy nierówność między średnimi (po drodze przegrupowując czynniki):
Ponownie używając nierówności między średnimi (wartości 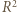 i
i 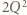 ), dostajemy oszacowanie
), dostajemy oszacowanie
czyli 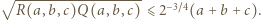 Stąd i z analogicznego oszacowania dla trójek
Stąd i z analogicznego oszacowania dla trójek 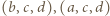 uzyskujemy kontynuację wcześniejszego ciągu nierówności:
uzyskujemy kontynuację wcześniejszego ciągu nierówności:
(bo 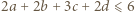 z założenia). Znaleziona wartość zostaje osiągnięta, gdy wszystkie nierówności stają się równościami; więc gdy
z założenia). Znaleziona wartość zostaje osiągnięta, gdy wszystkie nierówności stają się równościami; więc gdy 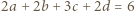 oraz
oraz
przy czym te trzy wartości też muszą być równe(!). To wymusza równości
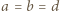
oraz
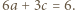
Ponadto - oznaczając krótko
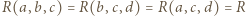
(i podobnie
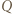
) - musimy mieć równość
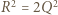
(do takiej pary też była stosowana nierówność między średnimi) - czyli
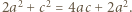
Wraz z równością
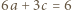
daje to alternatywę:
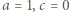
lub
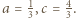
Dla czwórek
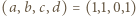
oraz
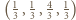
wyznaczone oszacowanie
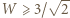
przechodzi w równość. Zatem szukane minimum wynosi
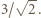
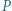 leży na boku
leży na boku 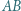 trójkąta
trójkąta 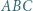 . Niech
. Niech 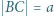 ,
, 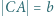 ,
, 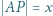 i
i 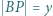 . Dowieść, że
. Dowieść, że 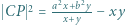 (twierdzenie Stewarta).
(twierdzenie Stewarta).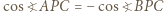 . Wyznaczyć lewą i prawą stronę z twierdzenia cosinusów dla trójkątów odpowiednio
. Wyznaczyć lewą i prawą stronę z twierdzenia cosinusów dla trójkątów odpowiednio 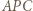 i
i 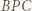 , a następnie przekształcić otrzymaną równość, by otrzymać
, a następnie przekształcić otrzymaną równość, by otrzymać 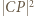 .
.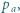
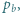
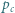 i
i 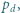 mające wspólny początek
mające wspólny początek 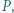 które zostały podane w kolejności antyzegarowej. Prosta
które zostały podane w kolejności antyzegarowej. Prosta 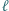 przecina je odpowiednio w punktach
przecina je odpowiednio w punktach 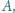
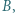
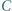 i
i 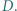 Dowieść, że wartość wyrażenia
Dowieść, że wartość wyrażenia 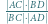 nie zależy od wyboru prostej
nie zależy od wyboru prostej 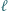 (niezmienniczość dwustosunku).
(niezmienniczość dwustosunku).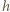 będzie odległością punktu
będzie odległością punktu 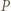 od prostej
od prostej 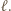 Oznaczmy przez
Oznaczmy przez 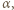
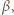
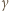 kąty pomiędzy półprostymi odpowiednio
kąty pomiędzy półprostymi odpowiednio 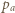 i
i 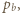
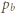 i
i 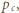
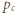 i
i 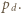 Wówczas obliczając na dwa sposoby pole trójkąta
Wówczas obliczając na dwa sposoby pole trójkąta 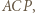 otrzymamy
otrzymamy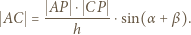
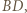
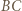 i
i 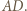
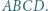 Punkty
Punkty 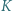 i
i 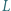 leżą odpowiednio na odcinkach
leżą odpowiednio na odcinkach 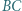 i
i 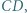 przy czym trójkąt
przy czym trójkąt 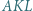 jest równoboczny. Dowieść, że suma pól trójkątów
jest równoboczny. Dowieść, że suma pól trójkątów 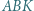 i
i 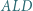 jest równa polu trójkąta
jest równa polu trójkąta 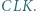
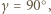 to
to ![1 [ABC] = 4 c2sin2α .](/math/temat/matematyka/geometria/zadania/2020/01/29/zm-20-02-kpo-4/2x-d78da09147956ae846d84f71c06c7431235d18c7-im-66,57,43-FF,FF,FF.gif) Niech
Niech 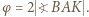 Zadanie sprowadza się do wykazania równości
Zadanie sprowadza się do wykazania równości 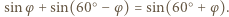
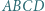 wpisany jest w okrąg. Na tym okręgu leży punkt
wpisany jest w okrąg. Na tym okręgu leży punkt 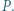 Udowodnić, że iloczyn odległości punktu
Udowodnić, że iloczyn odległości punktu 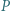 od prostych
od prostych 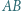 i
i 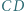 jest równy iloczynowi odległości punktu
jest równy iloczynowi odległości punktu 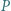 od prostych
od prostych 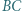 i
i 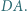
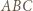 opuszczona z wierzchołka
opuszczona z wierzchołka 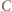 ma długość
ma długość 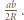 Odległości punktu
Odległości punktu 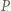 od prostych
od prostych 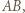
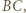
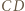 i
i 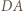 są odpowiednio wysokościami trójkątów
są odpowiednio wysokościami trójkątów 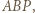
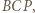
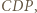
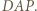
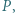
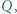
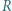 leżą odpowiednio na bokach
leżą odpowiednio na bokach 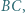
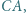
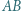 trójkąta
trójkąta 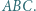 Spełnione są następujące równości:
Spełnione są następujące równości:
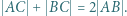
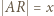 i
i 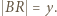 Obliczając pole trójkąta
Obliczając pole trójkąta 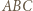 na dwa sposoby, otrzymamy równość
na dwa sposoby, otrzymamy równość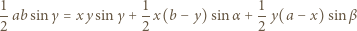
 i uprościć tę równość.
i uprościć tę równość. zachodzą następujące równości:
zachodzą następujące równości: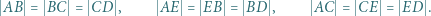
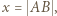
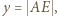
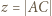 oraz
oraz 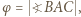
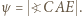 Z równości
Z równości 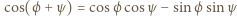 otrzymamy po przekształceniach
otrzymamy po przekształceniach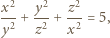
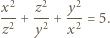
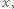
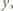
 są równe, a dzięki założeniu o wypukłości pięciokąta mamy
są równe, a dzięki założeniu o wypukłości pięciokąta mamy 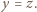 Dalszą część rozwiązania stanowią proste rachunki na kątach.
Dalszą część rozwiązania stanowią proste rachunki na kątach.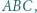 wpisanym w okrąg o środku
wpisanym w okrąg o środku 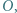 kąt przy wierzchołku
kąt przy wierzchołku 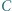 jest rozwarty oraz zachodzi równość
jest rozwarty oraz zachodzi równość 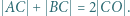 Odcinki
Odcinki 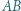 i
i 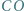 przecinają się w punkcie
przecinają się w punkcie 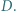 Dwusieczne kątów
Dwusieczne kątów 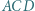 i
i 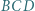 przecinają odcinek
przecinają odcinek 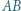 w punktach odpowiednio
w punktach odpowiednio 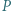 i
i 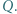 Dowieść, że punkt
Dowieść, że punkt 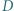 jest środkiem odcinka
jest środkiem odcinka 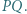
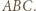 Z twierdzenia o dwusiecznej zastosowanego dla trójkąta
Z twierdzenia o dwusiecznej zastosowanego dla trójkąta 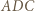 otrzymujemy
otrzymujemy 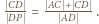 Miary kątów trójkąta
Miary kątów trójkąta 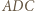 wynoszą odpowiednio
wynoszą odpowiednio 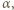
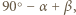
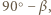 więc z twierdzenia sinusów
więc z twierdzenia sinusów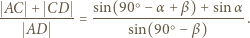
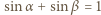 (treść zadania + twierdzenie sinusów), otrzymamy
(treść zadania + twierdzenie sinusów), otrzymamy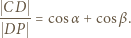
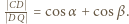
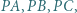 gdzie
gdzie 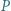 jest punktem wewnątrz trójkąta równobocznego
jest punktem wewnątrz trójkąta równobocznego 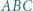 o boku 1.
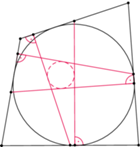
o boku 1.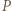 poprowadźmy proste równoległe do boków trójkąta
poprowadźmy proste równoległe do boków trójkąta 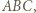 przecinające te boki w punktach
przecinające te boki w punktach 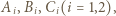 jak na rysunku. Wówczas
jak na rysunku. Wówczas 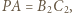 podobnie z długościami
podobnie z długościami 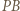 i
i 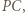 stąd należy zmaksymalizować pole trójkąta
stąd należy zmaksymalizować pole trójkąta 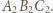 Oznaczając przez
Oznaczając przez ![[ |ℱ]](/math/temat/matematyka/geometria/planimetria/zadania/2019/12/31/zm-1626/8x-41db305196f42d3571e63f038f06f6638fa3e307-im-66,57,43-FF,FF,FF.gif) pole figury
pole figury 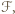 dostajemy
dostajemy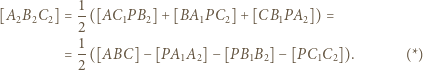
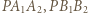 i
i 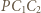 są podobne do
są podobne do 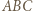 w skalach odpowiednio
w skalach odpowiednio 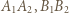 i
i 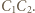 W związku z tym
W związku z tym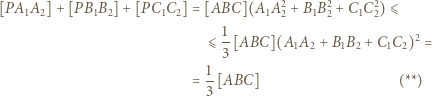
![|[A2B2C2]](/math/temat/matematyka/geometria/planimetria/zadania/2019/12/31/zm-1626/17x-41db305196f42d3571e63f038f06f6638fa3e307-im-66,57,43-FF,FF,FF.gif) Równość otrzymamy, biorąc za punkt
Równość otrzymamy, biorąc za punkt 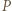 środek ciężkości trójkąta
środek ciężkości trójkąta 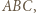 co kończy rozwiązanie.
co kończy rozwiązanie.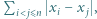 gdzie
gdzie ![x ∈[0,1] i](/math/temat/matematyka/analiza/zadania/2019/12/31/zm-1624/2x-7a859bc2426be6efd74caf08c9abc8e565add91b-im-2C,6B,73-FF,FF,FF.gif) dla
dla 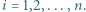
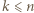 oraz dowolne wartości zmiennych
oraz dowolne wartości zmiennych ![x ∈[0,1] i](/math/temat/matematyka/analiza/zadania/2019/12/31/zm-1624/2x-e2b79e992298491a1812318ec88526ecbe876e9b-im-66,57,43-FF,FF,FF.gif) dla
dla 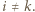 Wówczas wyrażenie
Wówczas wyrażenie 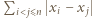 możemy traktować jako funkcję zmiennej
możemy traktować jako funkcję zmiennej 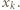 Jest to funkcja ściśle wypukła, jako suma ściśle wypukłych funkcji
Jest to funkcja ściśle wypukła, jako suma ściśle wypukłych funkcji 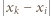 dla
dla 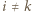 oraz stałych
oraz stałych 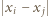 dla
dla 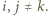 W tej sytuacji największa wartość tej funkcji jest przyjmowana na krańcach dziedziny, tj. dla
W tej sytuacji największa wartość tej funkcji jest przyjmowana na krańcach dziedziny, tj. dla 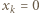 lub
lub 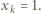 Z dowolności wyboru
Z dowolności wyboru 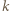 wnioskujemy, że największa wartość badanego wyrażenia jest przyjmowana dla pewnej konfiguracji
wnioskujemy, że największa wartość badanego wyrażenia jest przyjmowana dla pewnej konfiguracji 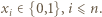 Jeśli
Jeśli 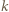 spośród zmiennych
spośród zmiennych 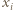 jest równe 1, to rozważana suma ma wartość
jest równe 1, to rozważana suma ma wartość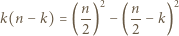
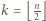 równą
równą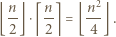
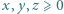 przyjmijmy:
przyjmijmy: 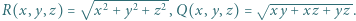 Wyznaczyć najmniejszą możliwą wartość wyrażenia
Wyznaczyć najmniejszą możliwą wartość wyrażenia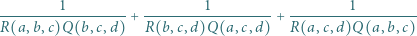
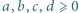 spełniających warunek
spełniających warunek 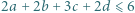 oraz wyznaczyć wszystkie czwórki
oraz wyznaczyć wszystkie czwórki 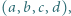 dla których to minimum jest osiągane.
dla których to minimum jest osiągane.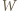 (stale zakładamy, że wszystkie mianowniki są dodatnie). Dwukrotnie stosujemy nierówność między średnimi (po drodze przegrupowując czynniki):
(stale zakładamy, że wszystkie mianowniki są dodatnie). Dwukrotnie stosujemy nierówność między średnimi (po drodze przegrupowując czynniki):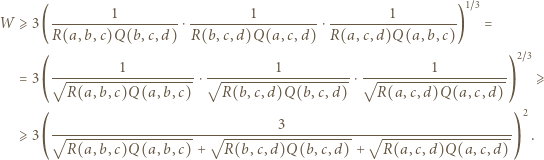
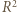 i
i 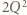 ), dostajemy oszacowanie
), dostajemy oszacowanie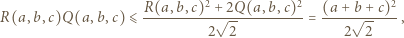
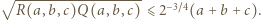 Stąd i z analogicznego oszacowania dla trójek
Stąd i z analogicznego oszacowania dla trójek 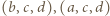 uzyskujemy kontynuację wcześniejszego ciągu nierówności:
uzyskujemy kontynuację wcześniejszego ciągu nierówności: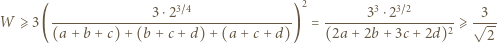
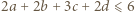 z założenia). Znaleziona wartość zostaje osiągnięta, gdy wszystkie nierówności stają się równościami; więc gdy
z założenia). Znaleziona wartość zostaje osiągnięta, gdy wszystkie nierówności stają się równościami; więc gdy 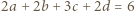 oraz
oraz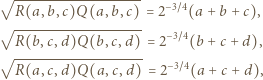
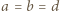 oraz
oraz 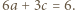 Ponadto - oznaczając krótko
Ponadto - oznaczając krótko 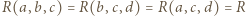 (i podobnie
(i podobnie 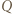 ) - musimy mieć równość
) - musimy mieć równość 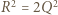 (do takiej pary też była stosowana nierówność między średnimi) - czyli
(do takiej pary też była stosowana nierówność między średnimi) - czyli 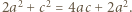 Wraz z równością
Wraz z równością 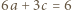 daje to alternatywę:
daje to alternatywę: 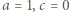 lub
lub 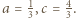 Dla czwórek
Dla czwórek 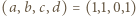 oraz
oraz 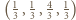 wyznaczone oszacowanie
wyznaczone oszacowanie 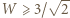 przechodzi w równość. Zatem szukane minimum wynosi
przechodzi w równość. Zatem szukane minimum wynosi 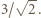
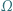 i
i 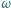 przecinają się w punktach
przecinają się w punktach 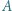 i
i 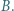 Środek
Środek 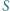 okręgu
okręgu 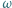 leży na okręgu
leży na okręgu 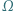 i jest końcem jego średnicy
i jest końcem jego średnicy 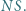 Cięciwa
Cięciwa 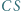 okręgu
okręgu 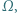 niebędąca średnicą, przecina okrąg
niebędąca średnicą, przecina okrąg 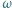 oraz odcinek
oraz odcinek 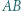 odpowiednio w punktach
odpowiednio w punktach 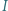 oraz
oraz 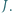 Prosta przechodząca przez
Prosta przechodząca przez 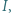 równoległa do
równoległa do 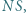 przecina odcinek
przecina odcinek 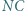 w punkcie
w punkcie 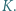 Dowieść, że prosta
Dowieść, że prosta 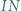 przechodzi przez środek odcinka
przechodzi przez środek odcinka 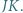

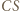 połowi kąt
połowi kąt 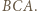 Leżący na nim punkt
Leżący na nim punkt 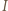 spełnia warunek
spełnia warunek 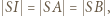 charakteryzujący środek okręgu wpisanego w trójkąt
charakteryzujący środek okręgu wpisanego w trójkąt 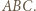 Trójkąt
Trójkąt 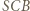 jest podobny do
jest podobny do 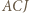 (równe kąty przy wierzchołkach
(równe kąty przy wierzchołkach 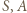 oraz
oraz 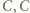 ). Otrzymujemy następujący ciąg proporcji (pierwsza z nich zachodzi, bo
). Otrzymujemy następujący ciąg proporcji (pierwsza z nich zachodzi, bo 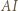 jest dwusieczną kąta
jest dwusieczną kąta 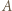 w trójkącie
w trójkącie 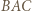 ; druga wynika ze wspomnianego podobieństwa; a ostatnia z równoległości
; druga wynika ze wspomnianego podobieństwa; a ostatnia z równoległości 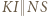 ):
):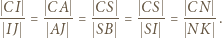
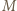 będzie punktem przecięcia prostych
będzie punktem przecięcia prostych 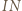 i
i 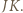 Wystarczy teraz zastosować twierdzenie Menelausa do trójkąta
Wystarczy teraz zastosować twierdzenie Menelausa do trójkąta 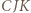 przeciętego prostą
przeciętego prostą 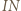 :
: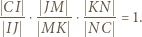
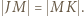
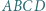 można wpisać okrąg. Przez środek każdego z odcinków
można wpisać okrąg. Przez środek każdego z odcinków 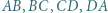 poprowadzono proste prostopadłe do przeciwległych boków czworokąta
poprowadzono proste prostopadłe do przeciwległych boków czworokąta 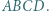 Proste te ograniczają obszar będący czworokątem wypukłym. Wykazać, że w ten czworokąt również można wpisać okrąg.
Proste te ograniczają obszar będący czworokątem wypukłym. Wykazać, że w ten czworokąt również można wpisać okrąg.
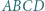 można opisać okrąg. Niech
można opisać okrąg. Niech 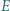 będzie punktem przecięcia przekątnych czworokąta. Załóżmy, że dwusieczna kąta
będzie punktem przecięcia przekątnych czworokąta. Załóżmy, że dwusieczna kąta 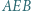 przecina prostą
przecina prostą 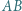 w punkcie
w punkcie 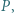 zaś prostą
zaś prostą 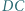 w punkcie
w punkcie 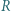 ; niech ponadto dwusieczna kąta
; niech ponadto dwusieczna kąta 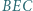 przecina prostą
przecina prostą 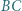 w punkcie
w punkcie 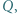 zaś prostą
zaś prostą 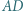 w punkcie
w punkcie 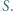 Udowodnić, że okręgi opisane na trójkątach
Udowodnić, że okręgi opisane na trójkątach 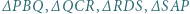 mają punkt wspólny.
mają punkt wspólny.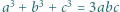 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 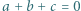 lub
lub 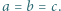
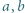 spełniają równość
spełniają równość 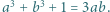 Wyznaczyć wszystkie możliwe wartości wyrażenia
Wyznaczyć wszystkie możliwe wartości wyrażenia 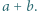
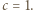 Są tu dwa przypadki do rozważania.
Są tu dwa przypadki do rozważania.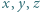 są rzeczywiste. Udowodnić, że jeśli
są rzeczywiste. Udowodnić, że jeśli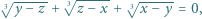
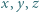 są równe.
są równe.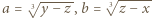 i
i 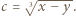
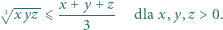
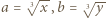 i
i 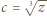 w tożsamości.
w tożsamości.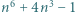 jest złożona dla każdej liczby całkowitej dodatniej
jest złożona dla każdej liczby całkowitej dodatniej 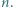
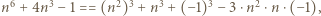 i użyć tożsamości (2) z artykułu dla
i użyć tożsamości (2) z artykułu dla 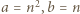 i
i 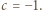
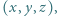 które spełniają równości
które spełniają równości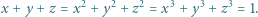
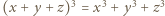 i dzięki tożsamości (1) z artykułu dochodzimy do wniosku, że wśród liczb
i dzięki tożsamości (1) z artykułu dochodzimy do wniosku, że wśród liczb 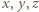 występuje co najmniej jedna para liczb przeciwnych.
występuje co najmniej jedna para liczb przeciwnych.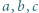 spełniają równość
spełniają równość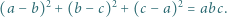
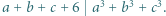
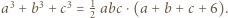 Wystarczy teraz wykazać, że co najmniej jedna z liczb
Wystarczy teraz wykazać, że co najmniej jedna z liczb 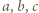 jest parzysta. To wynika z równości danej w zadaniu.
jest parzysta. To wynika z równości danej w zadaniu.