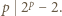Szły raz drogą trzy sześciany»Zadanie 8
o zadaniu...
- Zadanie pochodzi z artykułu Szły raz drogą trzy sześciany
- Publikacja w Delcie: styczeń 2020
- Publikacja elektroniczna: 31 grudnia 2019
- Artykuł źródłowy w wersji do druku [application/pdf]: (377 KB)
Liczby 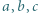 są całkowite. Wykazać, że jeśli liczba
są całkowite. Wykazać, że jeśli liczba 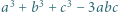 dzieli się przez 3, to dzieli się ona również przez 9.
dzieli się przez 3, to dzieli się ona również przez 9.
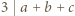 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 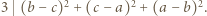 To ma miejsce dokładnie wtedy, gdy liczby
To ma miejsce dokładnie wtedy, gdy liczby 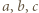 dają trzy jednakowe albo trzy różne reszty z dzielenia przez 3.
dają trzy jednakowe albo trzy różne reszty z dzielenia przez 3.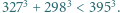 Uczynić to bez pomocy kalkulatora, wykonując przy tym możliwie najmniej rachunków.
Uczynić to bez pomocy kalkulatora, wykonując przy tym możliwie najmniej rachunków.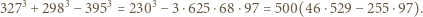
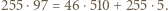
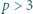 oraz takie liczby całkowite dodatnie
oraz takie liczby całkowite dodatnie 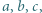 że
że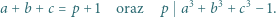
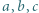 jest równa 1.
jest równa 1.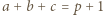 i
i 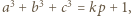 gdzie
gdzie 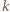 jest jakąś liczbą całkowitą. Wywnioskować stąd, że
jest jakąś liczbą całkowitą. Wywnioskować stąd, że 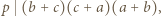 więc któryś z czynników dzieli się przez
więc któryś z czynników dzieli się przez 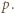 Te czynniki są dodatnie i nie przekraczają
Te czynniki są dodatnie i nie przekraczają 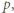 więc któryś z nich jest równy
więc któryś z nich jest równy 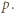
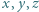 spełniają równość
spełniają równość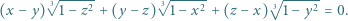
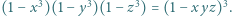
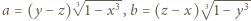 i
i 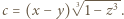 Następnie zauważyć, że
Następnie zauważyć, że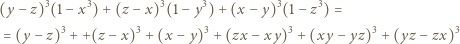
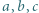 spełniają równość
spełniają równość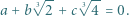
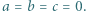
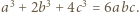 Wykazać kolejno, że
Wykazać kolejno, że 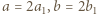 i
i 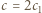 dla pewnych całkowitych
dla pewnych całkowitych 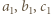 i zauważyć, że
i zauważyć, że 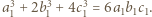 Następnie to samo rozumowanie zastosować do
Następnie to samo rozumowanie zastosować do 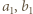 i
i 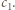 Ten proces można kontynuować w nieskończoność, co dowodzi, że każda potęga dwójki dzieli
Ten proces można kontynuować w nieskończoność, co dowodzi, że każda potęga dwójki dzieli 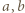 i
i 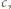 czyli
czyli 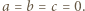
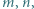 przy czym
przy czym 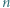 jest liczbą nieparzystą, większą niż
jest liczbą nieparzystą, większą niż 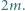 Udowodnić, że liczba
Udowodnić, że liczba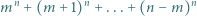
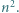
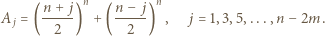
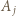 dzieli się przez
dzieli się przez 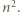 W rozwinięciu dwumianowym
W rozwinięciu dwumianowym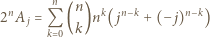
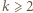 są podzielne przez
są podzielne przez 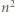 ; skoro zaś
; skoro zaś 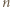 jest liczbą nieparzystą, dwa składniki początkowe dają w sumie
jest liczbą nieparzystą, dwa składniki początkowe dają w sumie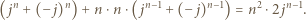
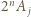 dzieli się przez
dzieli się przez 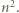 Korzystając jeszcze raz z nieparzystości
Korzystając jeszcze raz z nieparzystości 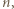 wnosimy, że
wnosimy, że 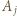 dzieli się przez
dzieli się przez 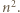
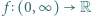 jest dana wzorem
jest dana wzorem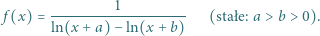
 ), i znaleźć równanie tej asymptoty.
), i znaleźć równanie tej asymptoty.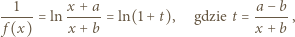
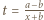 dąży do 0, gdy
dąży do 0, gdy 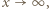 zatem
zatem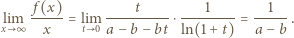
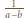 ; wystarczy zatem, by następująca różnica miała skończoną granicę (przy
; wystarczy zatem, by następująca różnica miała skończoną granicę (przy 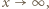 czyli
czyli 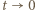 ):
):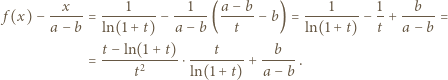
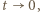 pierwszy z ilorazów (w ostatnim uzyskanym wyrażeniu) dąży do granicy 1/2 (bo
pierwszy z ilorazów (w ostatnim uzyskanym wyrażeniu) dąży do granicy 1/2 (bo 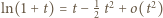 ). Stąd wniosek, że asymptotą (przy
). Stąd wniosek, że asymptotą (przy  ) jest prosta o równaniu
) jest prosta o równaniu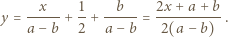
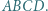 Punkty
Punkty 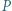 i
i 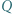 leżące odpowiednio wewnątrz trójkątów
leżące odpowiednio wewnątrz trójkątów 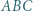 i
i 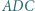 mają tę własność, że
mają tę własność, że 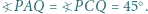 Wykazać, że
Wykazać, że
![[ℱ]](/math/temat/matematyka/geometria/planimetria/zadania/2019/11/29/zm-1623/8x-36c19e6efa8cca90b4ecde58a9ea9c818585cc21-im-2C,6B,73-FF,FF,FF.gif) oznacza pole figury
oznacza pole figury 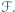
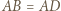 oraz
oraz 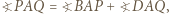 to istnieje punkt jednocześnie symetryczny do
to istnieje punkt jednocześnie symetryczny do 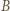 względem
względem 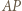 i do
i do 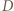 względem
względem 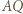 ; nazwijmy go
; nazwijmy go 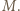 Skoro
Skoro ![|[ABP P]](/math/temat/matematyka/geometria/planimetria/zadania/2019/11/29/zm-1623/8x-9b94bf9272daebe741e8a2a4d8c739547e0d607b-im-66,57,43-FF,FF,FF.gif) oraz
oraz ![QQ]], |[AD](/math/temat/matematyka/geometria/planimetria/zadania/2019/11/29/zm-1623/9x-9b94bf9272daebe741e8a2a4d8c739547e0d607b-im-66,57,43-FF,FF,FF.gif) to lewa strona dowodzonej równości przybiera postać
to lewa strona dowodzonej równości przybiera postać 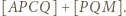
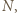 jednocześnie symetryczny do
jednocześnie symetryczny do 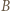 względem
względem 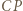 oraz do
oraz do 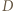 względem
względem 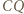 i podobnie prawą stronę dowodzonej równości można przepisać jako
i podobnie prawą stronę dowodzonej równości można przepisać jako 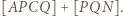 Do zakończenia rozwiązania wystarczy zauważyć, że trójkąty
Do zakończenia rozwiązania wystarczy zauważyć, że trójkąty 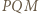 oraz
oraz 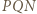 są przystające (cecha bok-bok-bok).
są przystające (cecha bok-bok-bok).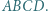 Punkty
Punkty 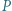 i
i 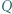 leżące odpowiednio wewnątrz trójkątów
leżące odpowiednio wewnątrz trójkątów 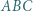 i
i 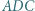 mają tę własność, że
mają tę własność, że 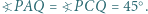 Wykazać, że
Wykazać, że 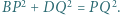
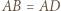 oraz
oraz 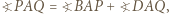 to istnieje punkt jednocześnie symetryczny do
to istnieje punkt jednocześnie symetryczny do 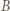 względem
względem 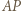 i do
i do 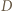 względem
względem 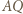 ; nazwijmy go
; nazwijmy go 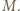 Trójkąt
Trójkąt 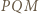 ma boki o długościach
ma boki o długościach 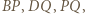 a jego kąt wewnętrzny przy wierzchołku
a jego kąt wewnętrzny przy wierzchołku 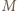 ma miarę
ma miarę 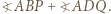
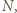 jednocześnie symetryczny do
jednocześnie symetryczny do 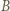 względem
względem 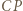 oraz do
oraz do 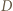 względem
względem 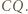 Trójkąt
Trójkąt 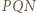 jest przystający do trójkąta
jest przystający do trójkąta 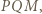 a kąt wewnętrzny przy wierzchołku
a kąt wewnętrzny przy wierzchołku 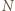 ma miarę
ma miarę 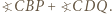 Pozostaje zauważyć, że
Pozostaje zauważyć, że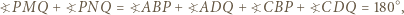
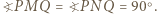 Teza zadania wynika więc z twierdzenia Pitagorasa zastosowanego do dowolnego z tych dwóch trójkątów.
Teza zadania wynika więc z twierdzenia Pitagorasa zastosowanego do dowolnego z tych dwóch trójkątów.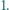 Jeśli na tablicy napisana jest co najmniej jedna z liczb
Jeśli na tablicy napisana jest co najmniej jedna z liczb 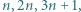 to można dopisać każdą z pozostałych. Rozstrzygnąć, czy każda dodatnia liczba całkowita może w pewnym momencie pojawić się na tablicy.
to można dopisać każdą z pozostałych. Rozstrzygnąć, czy każda dodatnia liczba całkowita może w pewnym momencie pojawić się na tablicy.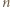 mogła zostać uzyskana (poprzez ciąg kilku kolejnych dopisywań) z pewnej mniejszej liczby. Stąd dostaniemy odpowiedź twierdzącą na postawione w zadaniu pytanie.
mogła zostać uzyskana (poprzez ciąg kilku kolejnych dopisywań) z pewnej mniejszej liczby. Stąd dostaniemy odpowiedź twierdzącą na postawione w zadaniu pytanie.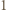 z dzielenia przez
z dzielenia przez 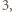 powiedzmy
powiedzmy 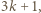 można uzyskać w jednym kroku z liczby
można uzyskać w jednym kroku z liczby 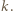 Liczba dająca resztę
Liczba dająca resztę 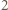 z dzielenia przez
z dzielenia przez 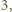 powiedzmy
powiedzmy 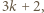 może zostać uzyskana w dwóch krokach z liczby
może zostać uzyskana w dwóch krokach z liczby 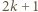 : w pierwszym kroku dopisujemy liczbę
: w pierwszym kroku dopisujemy liczbę 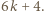 Wreszcie liczba podzielna przez
Wreszcie liczba podzielna przez 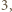 powiedzmy
powiedzmy 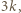 może zostać uzyskana w siedmiu krokach z liczby
może zostać uzyskana w siedmiu krokach z liczby 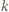 : w kolejnych pośrednich krokach dopisujemy
: w kolejnych pośrednich krokach dopisujemy 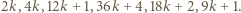
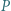 ma wszystkie współczynniki całkowite i dla każdej liczby naturalnej
ma wszystkie współczynniki całkowite i dla każdej liczby naturalnej 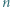 zachodzą nierówności
zachodzą nierówności 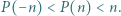 Wykazać, że
Wykazać, że 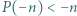 dla wszystkich naturalnych
dla wszystkich naturalnych 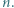
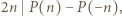 a z założeń
a z założeń 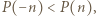 więc
więc 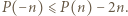
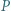 o współczynnikach całkowitych przyjmuje wartości nieparzyste dla pewnych dwóch kolejnych liczb naturalnych. Udowodnić, że ten wielomian nie ma pierwiastków będących liczbami całkowitymi.
o współczynnikach całkowitych przyjmuje wartości nieparzyste dla pewnych dwóch kolejnych liczb naturalnych. Udowodnić, że ten wielomian nie ma pierwiastków będących liczbami całkowitymi.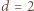 wywnioskujemy, że
wywnioskujemy, że 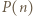 jest liczbą nieparzystą dla każdego całkowitego
jest liczbą nieparzystą dla każdego całkowitego 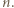
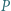 o współczynnikach całkowitych przyjmuje wartość
o współczynnikach całkowitych przyjmuje wartość 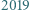 dla pięciu różnych argumentów będących liczbami całkowitymi. Dowieść, że ten wielomian nie ma pierwiastków całkowitych.
dla pięciu różnych argumentów będących liczbami całkowitymi. Dowieść, że ten wielomian nie ma pierwiastków całkowitych.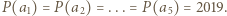 Liczby
Liczby 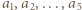 są różnymi pierwiastkami wielomianu
są różnymi pierwiastkami wielomianu 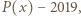 więc na mocy twierdzenia Bézouta
więc na mocy twierdzenia Bézouta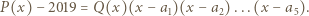
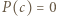 dla pewnego całkowitego
dla pewnego całkowitego 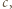 to liczba
to liczba 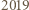 byłaby iloczynem sześciu liczb całkowitych, wśród których jest pięć różnych liczb.
byłaby iloczynem sześciu liczb całkowitych, wśród których jest pięć różnych liczb.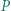 ma trzeci stopień i wszystkie współczynniki całkowite oraz spełnia równości:
ma trzeci stopień i wszystkie współczynniki całkowite oraz spełnia równości: 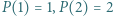 i
i 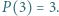 Wyznaczyć najmniejszą możliwą wartość
Wyznaczyć najmniejszą możliwą wartość 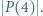
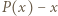 ma pierwiastki
ma pierwiastki 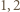 i
i 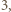 więc
więc 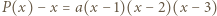 dla pewnego całkowitego
dla pewnego całkowitego 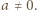
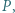 który ma czwarty stopień i spełnia równości:
który ma czwarty stopień i spełnia równości: 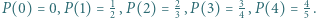
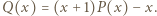 Jego pierwiastkami są
Jego pierwiastkami są 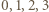 i
i 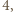 więc
więc 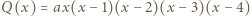 dla pewnego
dla pewnego 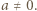 Liczba
Liczba 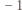 jest pierwiastkiem wielomianu
jest pierwiastkiem wielomianu 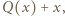 więc
więc 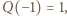 z czego wyznaczamy
z czego wyznaczamy 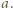
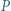 i
i 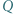 spełniają warunek
spełniają warunek 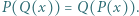 Wykazać, że wielomian
Wykazać, że wielomian 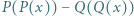 jest podzielny przez wielomian
jest podzielny przez wielomian 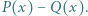
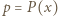 i
i 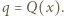 Mamy
Mamy 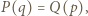 więc
więc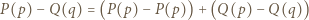
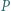 o współczynnikach całkowitych ma tę własność, że
o współczynnikach całkowitych ma tę własność, że 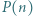 jest liczbą pierwszą dla wszystkich naturalnych
jest liczbą pierwszą dla wszystkich naturalnych 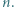 Dowieść, że
Dowieść, że 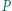 jest wielomianem stałym.
jest wielomianem stałym.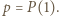 Na mocy twierdzenia
Na mocy twierdzenia 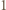 dla naturalnych
dla naturalnych 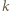 mamy
mamy 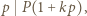 więc
więc 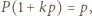 gdyż wartości
gdyż wartości 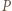 dla argumentów całkowitych są liczbami pierwszymi. Wielomian
dla argumentów całkowitych są liczbami pierwszymi. Wielomian 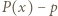 ma zatem nieskończenie wiele miejsc zerowych, więc jest zerowy.
ma zatem nieskończenie wiele miejsc zerowych, więc jest zerowy.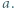 Niech
Niech 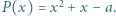 Udowodnić, że jeśli dla pewnego naturalnego
Udowodnić, że jeśli dla pewnego naturalnego 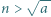 liczby
liczby 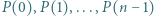 są względne pierwsze z
są względne pierwsze z 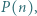 to liczba
to liczba 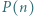 jest pierwsza.
jest pierwsza.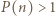 dla
dla 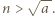 Przypuśćmy, że liczba
Przypuśćmy, że liczba 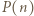 nie jest pierwsza. Wtedy ma ona dzielnik pierwszy
nie jest pierwsza. Wtedy ma ona dzielnik pierwszy 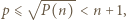 czyli
czyli 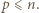 Wówczas
Wówczas 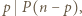 czyli
czyli 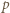 jest wspólnym dzielnikiem
jest wspólnym dzielnikiem 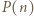 i
i 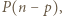 a to jest sprzeczne z założeniami.
a to jest sprzeczne z założeniami.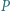 o współczynnikach całkowitych, spełniające warunek:
o współczynnikach całkowitych, spełniające warunek: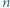 co najwyżej jedna z liczb
co najwyżej jedna z liczb 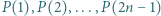 dzieli się przez
dzieli się przez 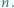
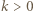 mamy
mamy 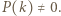 Niech
Niech 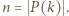 Ponieważ
Ponieważ 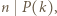 również
również 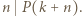 Zatem
Zatem 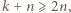 czyli
czyli 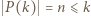 dla dużych
dla dużych 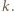 Stąd można wywnioskować, że
Stąd można wywnioskować, że 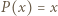 albo
albo 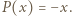
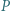 o współczynnikach całkowitych, które dla każdego naturalnego
o współczynnikach całkowitych, które dla każdego naturalnego 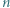 spełniają podzielność
spełniają podzielność 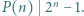
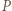 jest stały, to
jest stały, to 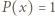 lub
lub 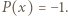 W przeciwnym razie dla pewnego
W przeciwnym razie dla pewnego 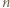 mamy
mamy 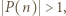 więc
więc 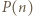 ma pewien dzielnik pierwszy
ma pewien dzielnik pierwszy 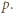 Mamy wtedy też
Mamy wtedy też 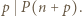 Zatem z założeń zadania
Zatem z założeń zadania 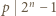 i
i 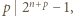 więc
więc 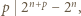 czyli
czyli 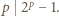 Jest to sprzeczne z małym twierdzeniem Fermata:
Jest to sprzeczne z małym twierdzeniem Fermata: