Zadanie ZM-1580
o zadaniu...
- Publikacja w Delcie: październik 2018
- Publikacja elektroniczna: 1 października 2018
Niech 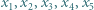 będą różnymi pierwiastkami wielomianu
będą różnymi pierwiastkami wielomianu 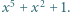 Wyznaczyć wartość wyrażenia
Wyznaczyć wartość wyrażenia
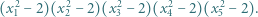
Niech 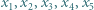 będą różnymi pierwiastkami wielomianu
będą różnymi pierwiastkami wielomianu 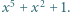 Wyznaczyć wartość wyrażenia
Wyznaczyć wartość wyrażenia
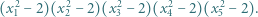
Zadanie 768 zaproponował pan Witold Bednarek z Łodzi.
Znaleźć wszystkie trójki liczb naturalnych 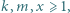 spełniające równanie
spełniające równanie
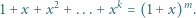 |
Jak wygrać (lub zremisować) w szachy z arcymistrzem, nawet nie umiejąc grać?
Czy istnieją takie liczby niewymierne 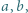 dla których liczba
dla których liczba 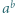 jest wymierna?
jest wymierna?
Jeśli szerokość pewnego prostokąta powiększyć o 50%, to jego szerokość powiększy się o 25%. O ile procent zmniejszy się długość tego prostokąta, jeśli jego długość zmniejszymy o 50%?
Rozważamy trójkąt równoboczny 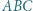 o boku
o boku 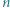 podzielony na
podzielony na 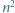 trójkątów równobocznych o boku
trójkątów równobocznych o boku 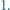 Każdy punkt, który jest wierzchołkiem co najmniej jednego z tych
Każdy punkt, który jest wierzchołkiem co najmniej jednego z tych 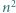 trójkątów, nazwijmy węzłem.
trójkątów, nazwijmy węzłem.
Wyznaczyć liczbę równoległoboków o wierzchołkach w węzłach, których dwa boki są równoległe do 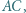 a dwa do
a dwa do 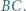
Rozważamy trójkąt równoboczny 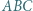 o boku
o boku 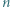 podzielony na
podzielony na 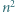 trójkątów równobocznych o boku
trójkątów równobocznych o boku 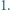 Każdy punkt, który jest wierzchołkiem co najmniej jednego z tych
Każdy punkt, który jest wierzchołkiem co najmniej jednego z tych 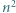 trójkątów, nazwijmy węzłem.
trójkątów, nazwijmy węzłem.
Wyznaczyć liczbę trójkątów równobocznych o wierzchołkach w węzłach (ale bokach niekoniecznie równoległych do boków 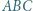 ).
).
Mając daną siatkę czworościanu, skonstruować punkty styczności sfery wpisanej w ten czworościan do jego ścian.
Zadanie 766 zaproponował pan Piotr Kumor z Olsztyna.
Znaleźć liczbę rzeczywistą 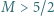 taką, że dla dowolnych liczb dodatnich
taką, że dla dowolnych liczb dodatnich 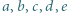 zachodzi nierówność
zachodzi nierówność
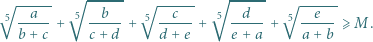 |
Im większa liczba 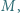 tym lepsze rozwiązanie.
tym lepsze rozwiązanie.
Czworokąt 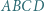 jest wpisany w okrąg. Jego najmniejszy kąt wewnętrzny ma wierzchołek
jest wpisany w okrąg. Jego najmniejszy kąt wewnętrzny ma wierzchołek 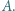 Zakładamy, że proste
Zakładamy, że proste 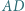 i
i 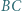 przecinają się w punkcie
przecinają się w punkcie 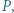 zaś proste
zaś proste 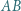 i
i 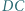 przecinają się w punkcie
przecinają się w punkcie 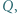 przy czym
przy czym 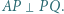 Niech
Niech 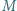 będzie środkiem przekątnej
będzie środkiem przekątnej 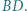 Wykazać, że
Wykazać, że 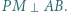
Wykaż, że wśród dowolnych 1111 parami różnych podzbiorów zbioru 11-elementowego zawsze znajdą się dwa rozłączne.
Udowodnij, że w dowolnym ciągu 2018 liczb całkowitych zawsze można wskazać pewną liczbę kolejnych wyrazów, których suma jest podzielna przez 2018.
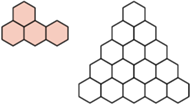
Płytką nazwiemy pokazaną na rysunku figurę złożoną z czterech sześciokątów foremnych o boku 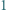 oraz dowolną figurę otrzymaną z niej przez obrót lub symetrię. Z kolei
oraz dowolną figurę otrzymaną z niej przez obrót lub symetrię. Z kolei 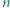 -trójkątem nazwiemy trójkątny układ tworzony przez
-trójkątem nazwiemy trójkątny układ tworzony przez 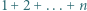 sześciokątów foremnych o boku
sześciokątów foremnych o boku 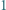 (na rysunku pokazano
(na rysunku pokazano 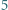 -trójkąt). Znaleźć wszystkie dodatnie liczby całkowite
-trójkąt). Znaleźć wszystkie dodatnie liczby całkowite 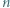 o tej własności, że z pewnej liczby płytek można ułożyć
o tej własności, że z pewnej liczby płytek można ułożyć 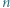 -trójkąt.
-trójkąt.
Dodatnią liczbę całkowitą  nazwiemy podkwadratową, jeżeli
nazwiemy podkwadratową, jeżeli 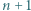 jest kwadratem liczby całkowitej. Wykazać, że istnieje nieskończenie wiele par liczb podkwadratowych o tej własności, że ich suma oraz iloczyn także są podkwadratowe.
jest kwadratem liczby całkowitej. Wykazać, że istnieje nieskończenie wiele par liczb podkwadratowych o tej własności, że ich suma oraz iloczyn także są podkwadratowe.
Wewnątrz kwadratu jednostkowego 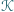 znajduje się wielokąt wypukły
znajduje się wielokąt wypukły 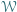 o polu większym od
o polu większym od 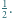 Wykazać, że wewnątrz wielokąta
Wykazać, że wewnątrz wielokąta 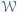 można wskazać odcinek o długości
można wskazać odcinek o długości  równoległy do boku kwadratu
równoległy do boku kwadratu 
Wykaż, że środkowa dzieli trójkąt na dwa trójkąty o równych polach.