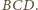Twierdzenie Cevy»Zadanie 3
o zadaniu...
- Zadanie pochodzi z artykułu Twierdzenie Cevy
- Publikacja w Delcie: luty 2011
- Publikacja elektroniczna: 01-02-2011
- Artykuł źródłowy w wersji do druku [application/pdf]: (75 KB)
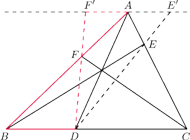
Punkty
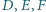 należą odpowiednio do boków
należą odpowiednio do boków
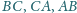 trójkąta
trójkąta
 proste
proste
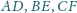 przecinają się w jednym
punkcie. Proste
przecinają się w jednym
punkcie. Proste
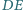 i
i
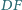 przecinają prostą równoległą do
przecinają prostą równoległą do
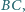 przechodzącą przez punkt
przechodzącą przez punkt
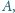 odpowiednio w punktach
odpowiednio w punktach
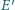 i
i
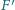 . Udowodnij, że punkt
. Udowodnij, że punkt
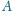 jest środkiem odcinka
jest środkiem odcinka
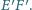
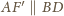 , to
, to
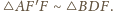 Stąd
Stąd


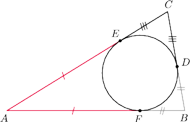
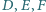 są punktami styczności okręgu wpisanego w trójkąt
są punktami styczności okręgu wpisanego w trójkąt
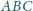 odpowiednio do boków
odpowiednio do boków
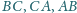 . Wykaż, że
proste
. Wykaż, że
proste
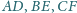 przecinają się w jednym punkcie (tzw. punkcie
Gergonne’a).
przecinają się w jednym punkcie (tzw. punkcie
Gergonne’a).
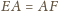 ,
,
 ,
,
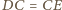 . Stąd
. Stąd
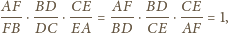

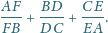
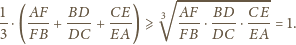
 w liczbach całkowitych
w liczbach całkowitych
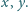
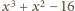 może dać
przy dzieleniu przez 7 wszystkie reszty z wyjątkiem 2 oraz 4. Potęgi dwójki
dają jedynie reszty 1, 2, 4. Rozważane równanie może więc być spełnione
tylko wtedy, gdy
może dać
przy dzieleniu przez 7 wszystkie reszty z wyjątkiem 2 oraz 4. Potęgi dwójki
dają jedynie reszty 1, 2, 4. Rozważane równanie może więc być spełnione
tylko wtedy, gdy
 ; to zaś ma miejsce jedynie dla
wykładników
; to zaś ma miejsce jedynie dla
wykładników
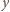 podzielnych przez 3.
podzielnych przez 3.
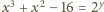 jest spełnione, to
jest spełnione, to
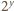 jest sześcianem liczby całkowitej. Dla liczb całkowitych
jest sześcianem liczby całkowitej. Dla liczb całkowitych
 wartość
wartość
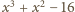 leży pomiędzy
leży pomiędzy
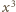 a
a
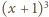 , więc
nie jest sześcianem. Dla
, więc
nie jest sześcianem. Dla
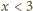 wartość
wartość
 jest
ujemna. Dla
jest
ujemna. Dla
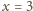 dostajemy równanie sprzeczne
dostajemy równanie sprzeczne
 .
Pozostaje wartość
.
Pozostaje wartość
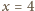 , która wraz z
, która wraz z
 daje jedyne
rozwiązanie równania.
daje jedyne
rozwiązanie równania.
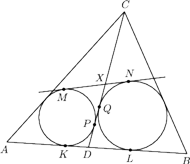
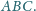 Rozważamy punkt
Rozważamy punkt
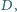 zmieniający swoje
położenie na boku
zmieniający swoje
położenie na boku
 Prosta styczna do okręgów wpisanych
w trójkąty
Prosta styczna do okręgów wpisanych
w trójkąty
 i
i
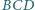 , rozłączna z odcinkiem
, rozłączna z odcinkiem
 przecina odcinek
przecina odcinek
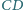 w punkcie
w punkcie
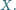 Udowodnić, że wszystkie
uzyskane w ten sposób punkty
Udowodnić, że wszystkie
uzyskane w ten sposób punkty
 leżą na pewnym okręgu.
leżą na pewnym okręgu.
 i
i
 są
styczne do boku
są
styczne do boku
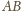 odpowiednio w punktach
odpowiednio w punktach
 i
i
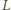 ;
do prostej przechodzącej przez
;
do prostej przechodzącej przez
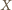 – odpowiednio w punktach
– odpowiednio w punktach
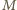 i
i
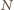 ; zaś do odcinka
; zaś do odcinka
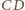 – odpowiednio w punktach
– odpowiednio w punktach
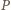 i
i
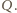
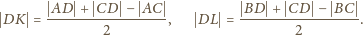

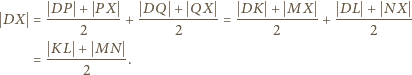
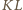 i
i
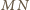 są symetryczne względem wspólnej osi
symetrii obu okręgów. Możemy zatem przepisać ostatnią równość jako
są symetryczne względem wspólnej osi
symetrii obu okręgów. Możemy zatem przepisać ostatnią równość jako
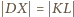 .
.
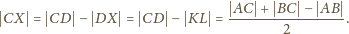
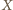 leży na okręgu o środku
leży na okręgu o środku
 i promieniu
zależnym jedynie od trójkąta
i promieniu
zależnym jedynie od trójkąta
 a nie od położenia punktu
a nie od położenia punktu
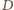 na boku
na boku
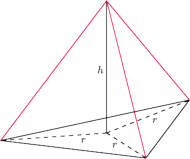
 oraz
długość krawędzi wychodzących z wierzchołka
oraz
długość krawędzi wychodzących z wierzchołka
 przez
przez
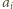 ,
gdzie
,
gdzie
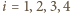 . Wtedy krawędź
. Wtedy krawędź
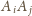 , gdzie
, gdzie
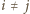 ,
wychodzi z wierzchołka
,
wychodzi z wierzchołka
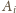 oraz z wierzchołka
oraz z wierzchołka
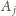 . Oznacza to,
że
. Oznacza to,
że
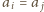 , a więc czworościan jest foremny.
, a więc czworościan jest foremny.
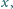 niecałkowite, dla których
wartość wyrażenia
niecałkowite, dla których
wartość wyrażenia
 jest liczbą całkowitą.
jest liczbą całkowitą.
 będzie jedną z szukanych liczb. Zapisujemy ją
w postaci nieskracalnego ułamka
będzie jedną z szukanych liczb. Zapisujemy ją
w postaci nieskracalnego ułamka
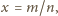 o mianowniku
o mianowniku
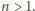 Liczba
Liczba
 ma być całkowita, co oznacza, że
ma być całkowita, co oznacza, że
 dzieli się przez
dzieli się przez
 Stąd w szczególności
wynika, że
Stąd w szczególności
wynika, że
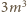 dzieli się przez
dzieli się przez
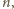 więc
więc
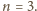 Zatem
Zatem
 dzieli się przez 27.
dzieli się przez 27.
 jest podzielna przez 27; innymi
słowy,
jest podzielna przez 27; innymi
słowy,
 dzieli się przez 9. Skoro zaś
dzieli się przez 9. Skoro zaś
 jest liczbą
względnie pierwszą z
jest liczbą
względnie pierwszą z
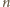 (czyli z 3), liczba
(czyli z 3), liczba
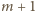 musi być
podzielna przez 9.
musi być
podzielna przez 9.
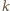 całkowitego mamy więc
całkowitego mamy więc
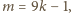 skąd
skąd
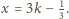 Na odwrót, gdy
Na odwrót, gdy
 ma taką postać, wówczas liczba
ma taką postać, wówczas liczba
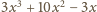 jest całkowita – o czym można się przekonać, analizując
„wstecz” wcześniejsze rozumowanie, albo po prostu sprawdzając rachunkiem,
że wartość tego wyrażenia wynosi
jest całkowita – o czym można się przekonać, analizując
„wstecz” wcześniejsze rozumowanie, albo po prostu sprawdzając rachunkiem,
że wartość tego wyrażenia wynosi
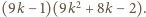
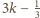 (
(
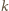 całkowite).
całkowite).








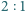 (licząc
od wierzchołków) leżą na jednej sferze.
(licząc
od wierzchołków) leżą na jednej sferze.
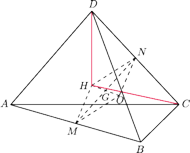
 niech
niech
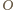 będzie
środkiem sfery opisanej, a
będzie
środkiem sfery opisanej, a
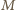 i
i
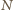 – środkami krawędzi
– środkami krawędzi
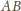 i
i
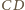 . Przez
. Przez
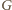 oznaczmy środek odcinka
oznaczmy środek odcinka
 ,
czyli środek ciężkości czworościanu
,
czyli środek ciężkości czworościanu
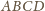 . Niech
. Niech
 będzie
punktem symetrycznym do
będzie
punktem symetrycznym do
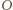 względem
względem
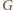 (rysunek). Punkty
(rysunek). Punkty
 leżą wtedy na jednej prostej, a
leżą wtedy na jednej prostej, a
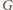 jest środkiem
odcinka
jest środkiem
odcinka
 . Wobec tego chcemy wykazać, że
. Wobec tego chcemy wykazać, że
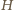 jest
ortocentrum czworościanu
jest
ortocentrum czworościanu
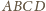 .
.
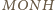 jest równoległobokiem.
W szczególności proste
jest równoległobokiem.
W szczególności proste
 i
i
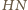 są równoległe. Z definicji
punktów
są równoległe. Z definicji
punktów
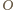 i
i
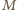 wynika, że odcinki
wynika, że odcinki
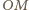 i
i
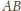 są
prostopadłe, więc również
są
prostopadłe, więc również
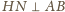 . Stąd i z prostopadłości
prostych
. Stąd i z prostopadłości
prostych
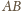 i
i
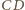 (
(
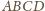 jest ortocentryczny!)
wynika, że płaszczyzna
jest ortocentryczny!)
wynika, że płaszczyzna
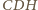 jest prostopadła do prostej
jest prostopadła do prostej
 .
W takim razie prosta
.
W takim razie prosta
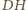 jest prostopadła do prostej
jest prostopadła do prostej
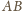 .
Analogicznie dowodzimy, że
.
Analogicznie dowodzimy, że
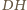 jest prostopadła również do
prostej
jest prostopadła również do
prostej
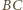 .
.
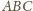 , czyli
stanowi wysokość czworościanu
, czyli
stanowi wysokość czworościanu
 . Podobnie dowodzimy, że
proste
. Podobnie dowodzimy, że
proste
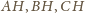 są wysokościami rozpatrywanego czworościanu, co
kończy dowód.
są wysokościami rozpatrywanego czworościanu, co
kończy dowód.
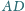 czworościanu
czworościanu
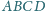 jest prostopadła do
płaszczyzny
jest prostopadła do
płaszczyzny
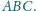 Wykazać, że rzut prostokątny ortocentrum
trójkąta
Wykazać, że rzut prostokątny ortocentrum
trójkąta
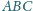 na płaszczyznę
na płaszczyznę
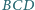 jest ortocentrum trójkąta
jest ortocentrum trójkąta
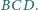
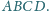 Dowieść, że krawędzie
Dowieść, że krawędzie
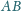 i
i
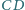 są prostopadłe wtedy i tylko wtedy, gdy istnieje w przestrzeni
taki równoległobok
są prostopadłe wtedy i tylko wtedy, gdy istnieje w przestrzeni
taki równoległobok
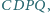 że
że
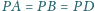 oraz
oraz


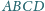 wysokości
poprowadzone z wierzchołków
wysokości
poprowadzone z wierzchołków
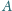 i
i
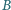 przecinają się, to również
wysokości poprowadzone z wierzchołków
przecinają się, to również
wysokości poprowadzone z wierzchołków
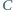 i
i
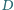 przecinają
się.
przecinają
się.
 będzie punktem przecięcia wysokości czworościanu
poprowadzonych z wierzchołków
będzie punktem przecięcia wysokości czworościanu
poprowadzonych z wierzchołków
 i
i
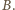 Mamy
Mamy
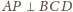 ,
więc też
,
więc też
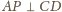 i analogicznie
i analogicznie
 . W takim razie
płaszczyzna
. W takim razie
płaszczyzna
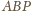 jest prostopadła do krawędzi
jest prostopadła do krawędzi
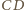 , w szczególności
, w szczególności
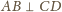 . Na prostej
. Na prostej
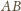 wybierzmy taki punkt
wybierzmy taki punkt
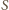 , że
, że
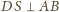 . Zatem płaszczyzna
. Zatem płaszczyzna
 jest prostopadła do krawędzi
jest prostopadła do krawędzi
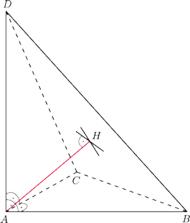
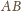 . Niech
. Niech
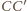 i
i
 będą wysokościami trójkąta
będą wysokościami trójkąta
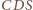 (rysunek obok). Prosta
(rysunek obok). Prosta
 jest prostopadła zarówno
do
jest prostopadła zarówno
do
 , jak i do
, jak i do
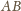 (bo leży w płaszczyźnie prostopadłej
do tej krawędzi). Jest więc wysokością czworościanu
(bo leży w płaszczyźnie prostopadłej
do tej krawędzi). Jest więc wysokością czworościanu
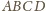 poprowadzoną z wierzchołka
poprowadzoną z wierzchołka
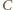 . Analogicznie dowodzimy, że również
. Analogicznie dowodzimy, że również
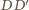 jest wysokością danego czworościanu. Te dwie proste mają punkt
wspólny będący ortocentrum trójkąta
jest wysokością danego czworościanu. Te dwie proste mają punkt
wspólny będący ortocentrum trójkąta
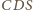 . Dowód jest więc
zakończony.
. Dowód jest więc
zakończony.
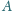 czworościanu
czworościanu
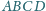 są proste. Wykazać, że rzut prostokątny
są proste. Wykazać, że rzut prostokątny
 punktu
punktu
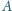 na
płaszczyznę
na
płaszczyznę
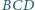 jest ortocentrum trójkąta
jest ortocentrum trójkąta
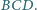
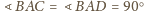 , to
, to
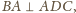 a więc
a więc
 Ponadto
Ponadto
 skąd
skąd
 Zatem płaszczyzna
Zatem płaszczyzna
 jest prostopadła do prostej
jest prostopadła do prostej
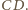 W takim razie
W takim razie
 .
Analogicznie udowodnimy, że
.
Analogicznie udowodnimy, że
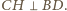 Zatem punkt
Zatem punkt
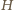 jest
ortocentrum trójkąta
jest
ortocentrum trójkąta