Niby nic»Zadanie 1
Punkty 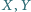 są środkami odpowiednio boków
są środkami odpowiednio boków 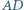 i
i 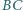 czworokąta wypukłego
czworokąta wypukłego 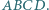 Udowodnij, że
Udowodnij, że 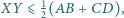 przy czym równość zachodzi wtedy i tylko wtedy, gdy
przy czym równość zachodzi wtedy i tylko wtedy, gdy 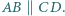
Punkty 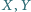 są środkami odpowiednio boków
są środkami odpowiednio boków 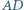 i
i 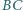 czworokąta wypukłego
czworokąta wypukłego 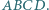 Udowodnij, że
Udowodnij, że 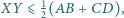 przy czym równość zachodzi wtedy i tylko wtedy, gdy
przy czym równość zachodzi wtedy i tylko wtedy, gdy 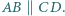
Na bokach 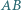 i
i 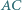 trójkąta
trójkąta 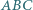 zbudowano, po jego zewnętrznej stronie, kwadraty
zbudowano, po jego zewnętrznej stronie, kwadraty 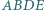 i
i 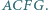 Punkty
Punkty 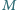 i
i 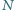 są odpowiednio środkami odcinków
są odpowiednio środkami odcinków 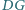 i
i 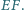 Wyznacz możliwe wartości wyrażenia
Wyznacz możliwe wartości wyrażenia 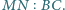
Przekątne 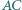 i
i 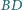 czworokąta wypukłego
czworokąta wypukłego 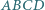 są równej długości. Punkty
są równej długości. Punkty 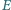 i
i 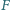 są odpowiednio środkami boków
są odpowiednio środkami boków 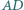 i
i 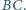 Udowodnij, że prosta
Udowodnij, że prosta 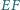 tworzy równe kąty z przekątnymi
tworzy równe kąty z przekątnymi 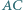 i
i 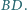
Czworokąt 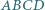 nie jest równoległobokiem oraz
nie jest równoległobokiem oraz 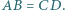 Punkty
Punkty 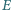 i
i 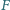 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 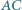 i
i 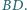 Wykaż, że rzuty prostopadłe odcinków
Wykaż, że rzuty prostopadłe odcinków 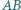 i
i 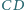 na prostą
na prostą 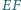 są równej długości.
są równej długości.
W sześciokącie wypukłym 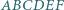 o polu 1 punkty
o polu 1 punkty 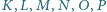 są środkami odpowiednio przekątnych
są środkami odpowiednio przekątnych 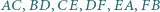 i tworzą sześciokąt wypukły
i tworzą sześciokąt wypukły 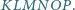 Wyznacz jego pole.
Wyznacz jego pole.
Niech 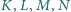 będą środkami kolejnych boków czworokąta
będą środkami kolejnych boków czworokąta 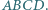 Wykaż, że
Wykaż, że 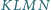 jest równoległobokiem, że
jest równoległobokiem, że 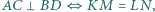 że
że 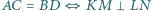 oraz wyznacz stosunek pól
oraz wyznacz stosunek pól ![N] [ABCD]. [KLM](/math/temat/matematyka/geometria/planimetria/zadania/2017/04/29/zm-17_05-deltoid-6/6x-476c50773c7ee85da9c32be7747c5f72357fd03b-im-2C,6B,73-FF,FF,FF.gif)
Dany jest trójkąt 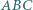 o bokach
o bokach 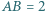 oraz
oraz 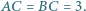 Punkt
Punkt 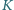 jest środkiem boku
jest środkiem boku 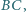 punkt
punkt 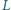 leży na boku
leży na boku 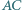 oraz
oraz 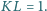 Wyznacz długość odcinka
Wyznacz długość odcinka 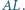
Niech 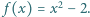 Udowodnić, że dla każdego
Udowodnić, że dla każdego 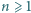 równanie
równanie
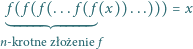
ma 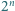 różnych rozwiązań rzeczywistych.
różnych rozwiązań rzeczywistych.
Udowodnić, że jeżeli dla pewnej liczby naturalnej 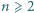 liczba
liczba 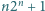 jest pierwsza, to liczby
jest pierwsza, to liczby 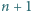 oraz
oraz 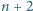 są złożone.
są złożone.
Zadanie 740 zaproponował pan Witold Bednarek z Łodzi.
Obliczyć kres dolny wartości sumy
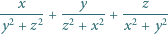
gdy  mogą być dowolnymi liczbami dodatnimi, spełniającymi warunek
mogą być dowolnymi liczbami dodatnimi, spełniającymi warunek 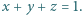
Znaleźć wszystkie funkcje 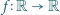 o następujących własnościach:
o następujących własnościach:
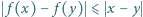 dla
dla 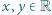 ;
;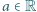 ciąg
ciąg 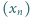 określony wzorami
określony wzorami 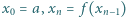 (dla
(dla 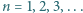 ) jest ciągiem arytmetycznym.
) jest ciągiem arytmetycznym.Czy w sześcianie o krawędzi 20 zmieści się kwadrat o boku 21?
Czy w sześcianie o krawędzi 20 można wywiercić tunel, przez który da się przesunąć sześcian o krawędzi 21?
Wyznacz liczbę podzbiorów zbioru 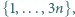 które nie zawierają dwóch liczb różniących się o
które nie zawierają dwóch liczb różniących się o 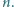
Udowodnij tożsamość 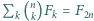 (
( 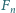 oznacza
oznacza  -tą liczbę Fibonacciego, czyli rozwiązanie równania rekurencyjnego
-tą liczbę Fibonacciego, czyli rozwiązanie równania rekurencyjnego 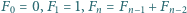 dla
dla 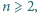 a zarazem liczbę pokryć paska
a zarazem liczbę pokryć paska 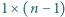 kwadratami
kwadratami 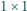 i prostokątami
i prostokątami 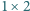 ).
).
Udowodnić, że dla każdego 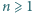 istnieje ciąg arytmetyczny
istnieje ciąg arytmetyczny  dodatnich liczb całkowitych, z których każda jest podzielna przez sumę swoich cyfr (w zapisie dziesiętnym).
dodatnich liczb całkowitych, z których każda jest podzielna przez sumę swoich cyfr (w zapisie dziesiętnym).
Wskazówka. W rozwiązaniu można skorzystać z twierdzenia o liczbach pierwszych, na przykład używając szacowania 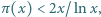 prawdziwego dla dostatecznie dużych
prawdziwego dla dostatecznie dużych 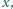 gdzie
gdzie 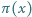 oznacza liczbę liczb pierwszych nie większych od
oznacza liczbę liczb pierwszych nie większych od 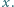
Wielokąt wypukły został podzielony odcinkami na skończoną liczbę czworokątów. Udowodnić, że co najmniej jeden z nich jest wypukły.
Zadanie 738 zaproponował pan Bartłomiej Pawlik z Limanowej.
Wypisując, jedna za drugą, wszystkie liczby całkowite dodatnie, mające (w systemie dziesiętnym) co najwyżej 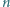 cyfr, piszemy łącznie
cyfr, piszemy łącznie 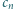 cyfr (np.
cyfr (np. 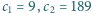 ); w tym
); w tym 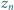 zer (np.
zer (np. 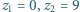 ). Czy równość
). Czy równość 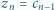 jest spełniona dla wszystkich liczb naturalnych
jest spełniona dla wszystkich liczb naturalnych 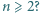
Pięciokąt 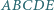 jest wpisany w okrąg
jest wpisany w okrąg 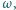 przy czym proste
przy czym proste 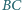 i
i 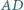 przecinają się w takim punkcie
przecinają się w takim punkcie 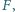 że prosta
że prosta 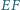 jest styczna do
jest styczna do 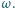 Druga prosta styczna do okręgu
Druga prosta styczna do okręgu 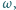 równoległa do
równoległa do 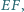 przecina proste
przecina proste 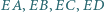 odpowiednio w punktach
odpowiednio w punktach 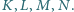 Udowodnić, że odcinki
Udowodnić, że odcinki 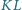 i
i 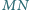 mają jednakową długość.
mają jednakową długość.
Przypuśćmy, że dla pewnej dodatniej liczby całkowitej 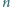 liczby
liczby 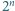 oraz
oraz 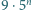 rozpoczynają się w zapisie dziesiętnym tą samą cyfrą. Jaka to cyfra?
rozpoczynają się w zapisie dziesiętnym tą samą cyfrą. Jaka to cyfra?