Zadanie ZM-1369
o zadaniu...
- Publikacja w Delcie: wrzesień 2013
- Publikacja elektroniczna: 31-08-2013
Znaleźć wszystkie funkcje
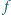 postaci
postaci
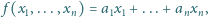
dla pewnych
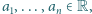 które na zbiorze
które na zbiorze
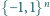 przyjmują
tylko dwie wartości:
przyjmują
tylko dwie wartości:
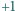 lub
lub
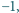 tzn. takie, że jeśli
tzn. takie, że jeśli
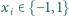 dla
dla
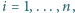 to
to
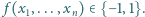
Niech wielomian
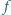 postaci
postaci
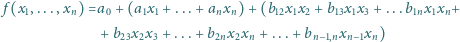
przyjmuje na zbiorze
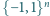 tylko dwie wartości
tylko dwie wartości
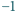 lub
lub
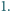 Udowodnić, że suma kwadratów jego współczynników wynosi
Udowodnić, że suma kwadratów jego współczynników wynosi
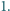
Czy istnieje wielomian
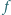 zadany wzorem
zadany wzorem
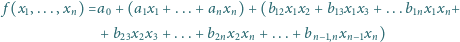
taki że dokładnie trzy spośród jego współczynników
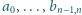 są
niezerowe, i o tej własności, że na zbiorze
są
niezerowe, i o tej własności, że na zbiorze
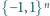 przyjmuje on tylko
wartości
przyjmuje on tylko
wartości
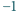 i
i
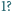 A jeśli założymy, że dokładnie cztery
współczynniki mają być niezerowe?
A jeśli założymy, że dokładnie cztery
współczynniki mają być niezerowe?
Udowodnić, że równanie
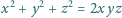
nie ma rozwiązania w liczbach całkowitych dodatnich.
Dana jest liczba wymierna
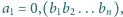 w której zapisie
dziesiętnym blok cyfr
w której zapisie
dziesiętnym blok cyfr
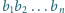 powtarza się okresowo po przecinku.
Rozważmy liczby
powtarza się okresowo po przecinku.
Rozważmy liczby
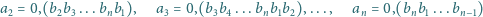
powstałe z
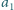 przez cykliczne przesunięcia cyfr w bloku. Udowodnić,
że
przez cykliczne przesunięcia cyfr w bloku. Udowodnić,
że
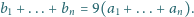
Zadanie 664 zaproponował pan Tomasz Ordowski
Dowieść, że jeśli liczba rzeczywista
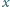 spełnia równanie
spełnia równanie
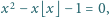 to każda potęga liczby
to każda potęga liczby
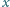 o wykładniku
dodatnim nieparzystym także spełnia to równanie.
o wykładniku
dodatnim nieparzystym także spełnia to równanie.
Czy istnieje nieskończony, ściśle rosnący ciąg liczb naturalnych
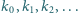 taki, że dla każdego
taki, że dla każdego
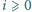 iloczyn
iloczyn
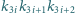 jest
podzielny przez każdą z liczb
jest
podzielny przez każdą z liczb
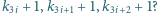
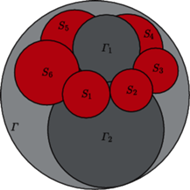
Szare sfery są parami styczne i każda z nich styczna jest do każdej z kolorowych sfer, tworzących łańcuch.
Styczne zewnętrznie sfery
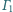 i
i
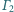 są styczne wewnętrznie do sfery
są styczne wewnętrznie do sfery
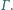 Do każdej z tych trzech sfer styczna jest każda z
Do każdej z tych trzech sfer styczna jest każda z
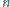 sfer
sfer
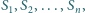 ponadto dla każdego
ponadto dla każdego
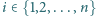 sfera
sfera
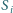 styczna jest do sfery
styczna jest do sfery
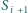 (przy czym
(przy czym
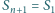 ). Dla jakich
). Dla jakich
 istnieje taki łańcuch sfer
istnieje taki łańcuch sfer
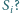 W jaki sposób zależy to od
rozmiarów i wzajemnego położenia sfer
W jaki sposób zależy to od
rozmiarów i wzajemnego położenia sfer
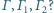 Czy i jak zależy to
od wyboru początkowej sfery
Czy i jak zależy to
od wyboru początkowej sfery
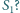
Na płaszczyźnie dane są rozłączne wewnętrznie okręgi
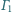 i
i
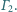 Do
każdego z nich styczny jest każdy z
Do
każdego z nich styczny jest każdy z
 okręgów
okręgów
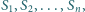 ponadto
dla każdego
ponadto
dla każdego
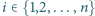 okrąg
okrąg
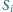 styczny jest do okręgu
styczny jest do okręgu
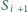 (przy czym
(przy czym
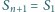 ). Dla jakich
). Dla jakich
 istnieje taki łańcuch
okręgów
istnieje taki łańcuch
okręgów
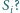 W jaki sposób zależy to od rozmiarów i wzajemnego
położenia okręgów
W jaki sposób zależy to od rozmiarów i wzajemnego
położenia okręgów
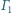 i
i
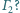 Czy i jak zależy to od wyboru
początkowego okręgu
Czy i jak zależy to od wyboru
początkowego okręgu
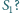
Dany jest czworościan
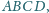 w którym
w którym
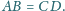 Ponadto
suma pól ścian
Ponadto
suma pól ścian
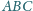 i
i
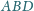 jest równa sumie pól
ścian
jest równa sumie pól
ścian
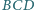 i
i
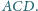 Dowieść, że
Dowieść, że
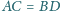 lub
lub
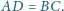
Zadanie zawodów II stopnia
Czy istnieje taki trójkat ostrokątny, w którym długości wszystkich boków i wszystkich wysokości są liczbami całkowitymi? Odpowiedź uzasadnij.
Wielomian
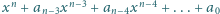 ma współczynniki
rzeczywiste
ma współczynniki
rzeczywiste
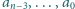 nie wszystkie równe
nie wszystkie równe
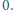 Udowodnić, że
ma on mniej niż
Udowodnić, że
ma on mniej niż
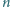 pierwiastków rzeczywistych.
pierwiastków rzeczywistych.
Udowodnić, że istnieje liczba
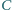 o następującej własności: jeśli
równanie
o następującej własności: jeśli
równanie
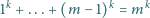
ma rozwiązanie dla pewnych liczb naturalnych
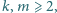 to
to
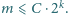
Zadanie 662 zaproponował pan Paweł Najman z Krakowa. Jest to kontynuacja zadania 654.
Ciąg
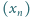 jest określony wzorem rekurencyjnym
jest określony wzorem rekurencyjnym
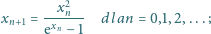
wyraz początkowy
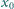 jest dowolną liczbą dodatnią. Obliczyć
granicę
jest dowolną liczbą dodatnią. Obliczyć
granicę
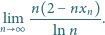
Wyznacz obraz kwadratu opisanego na okręgu w inwersji względem tego okręgu.
Okrąg o środku w punkcie
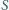 i wpisany w czworokąt wypukły
i wpisany w czworokąt wypukły
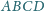 jest styczny do boków
jest styczny do boków
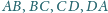 odpowiednio
w punktach
odpowiednio
w punktach
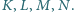 Proste
Proste
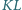 i
i
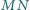 przecinają
się w punkcie
przecinają
się w punkcie
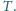 Wykaż, że proste
Wykaż, że proste
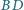 i
i
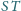 są
prostopadłe.
są
prostopadłe.
Każdy z rozłącznych okręgów
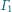 i
i
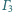 jest styczny zewnętrznie
do każdego z rozłącznych okręgów
jest styczny zewnętrznie
do każdego z rozłącznych okręgów
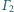 i
i
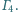 Wykaż, że punkty
styczności leżą na jednym okręgu.
Wykaż, że punkty
styczności leżą na jednym okręgu.