Wielkie granie
O pewnej sztuczce
Jakiś czas temu pokazano mi pewną sztuczkę karcianą. Pokazywały ją dwie osoby, Karol i Marcin. Najpierw Karol dostał pięć kart wylosowanych z talii. Nie pokazując ich nikomu, wybrał jedną z nich i ukrył przed wszystkimi.Pozostałe cztery ułożył w wybranej przez siebie kolejności i pokazał Marcinowi. Wtedy ten bezbłędnie odgadł, jaka jest piąta, ukryta karta.
Obliczmy. Marcinowi została zaprezentowana pewna permutacja czteroelementowego
zbioru kart. Takich permutacji jest
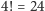 . Następnie odgadł pozostałą,
ukrytą kartę. W talii są
. Następnie odgadł pozostałą,
ukrytą kartę. W talii są
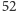 karty, on widzi
karty, on widzi
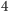 z nich, więc pozostaje
z nich, więc pozostaje
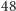 możliwości. Czyli Marcin dostał
możliwości. Czyli Marcin dostał
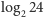 bitów informacji,
a do podjęcia decyzji potrzebuje
bitów informacji,
a do podjęcia decyzji potrzebuje
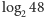 bitów. Proste odejmowanie,
bitów. Proste odejmowanie,
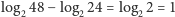 , dowodzi, że Marcin ma dokładnie o bit
informacji za mało!
, dowodzi, że Marcin ma dokładnie o bit
informacji za mało!
W czasie gdy liczyliśmy, oni pokazali sztuczkę następnych kilka razy i zawsze się udawała. W naszych obliczeniach pominęliśmy fakt, że Karol własnoręcznie wybierał tę jedną kartę spośród pięciu. Ale jak wybór Karola może przekazać bit informacji Marcinowi?
Poniżej zaprezentowane jest przykładowe rozwiązanie, jednak przed jego przeczytaniem polecam poszukać własnego.
Rozwiązanie okazuje się (jak zwykle) proste, chociaż (jak zwykle) trudno na nie
wpaść. Najpierw opiszę działanie od strony Karola. Dostałem pięć
kart. Wśród nich któryś kolor musi występować przynajmniej dwa
razy. Powiedzmy, że ten kolor to pik i mamy do czynienia z dwiema
kartami w tym kolorze (jeżeli jest ich więcej, to bierzemy pod uwagę tylko
dwie). Mówiąc nieściśle, wybieram tę z nich, od której jest bliżej do
drugiej, idąc cyklicznie w górę (2, 3, …król, as, 2, 3,...). Ściślej, kartom
od dwójki do asa przypiszmy liczby od
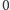 do
do
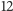 i liczby
odpowiadające naszym dwóm pikom oznaczmy
i liczby
odpowiadające naszym dwóm pikom oznaczmy
 i
i
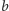 . Oznaczmy
. Oznaczmy
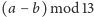 przez
przez
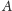 i
i
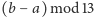 przez
przez
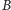 .
Oczywiście,
.
Oczywiście,
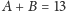 , obie są dodatnie, więc któraś z nich
jest mniejsza niż
, obie są dodatnie, więc któraś z nich
jest mniejsza niż
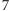 . Z symetrii mogę założyć, że
. Z symetrii mogę założyć, że
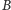 .
W takim przypadku wybieram kartę odpowiadającą liczbie
.
W takim przypadku wybieram kartę odpowiadającą liczbie
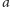 i mam
gwarancję, że druga z nich nie jest dalej niż
i mam
gwarancję, że druga z nich nie jest dalej niż
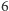 kart „do przodu” (bo
kart „do przodu” (bo
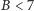 ). Teraz pora na permutację, którą przekażę Marcinowi. Pozostały
z dwóch pików kładę jako pierwszy, pozostałe trzy karty permutuję według
ustalonego algorytmu, tak by zakodować liczbę
). Teraz pora na permutację, którą przekażę Marcinowi. Pozostały
z dwóch pików kładę jako pierwszy, pozostałe trzy karty permutuję według
ustalonego algorytmu, tak by zakodować liczbę
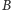 . To się uda,
ponieważ permutacji jest
. To się uda,
ponieważ permutacji jest
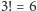 , a
, a
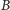 jest jedną z liczb
jest jedną z liczb
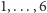 .
.
Przykładowa metoda kodowania liczb za pomocą permutacji może wyglądać
następująco. Mamy do użycia
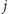 kart i chcemy za ich pomocą zakodować
jedną spośród liczb
kart i chcemy za ich pomocą zakodować
jedną spośród liczb
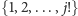 , oznaczmy ją
, oznaczmy ją
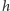 . Przyjmijmy,
że karty te są posegregowane według ich rangi
. Przyjmijmy,
że karty te są posegregowane według ich rangi
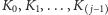 .
Weźmy kartę
.
Weźmy kartę
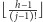 i połóżmy ją jako pierwszą w permutacji.
Następnie za pomocą pozostałych kart zakodujmy indukcyjnie liczbę
i połóżmy ją jako pierwszą w permutacji.
Następnie za pomocą pozostałych kart zakodujmy indukcyjnie liczbę
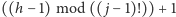 jako permutację pozostałych
jako permutację pozostałych
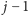 kart.
Oczywiście, indukcja ta się kończy, gdy mamy zakodować pojedynczą kartą
liczbę
kart.
Oczywiście, indukcja ta się kończy, gdy mamy zakodować pojedynczą kartą
liczbę
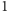 , co wykonujemy, po prostu kładąc kartę na stole.
, co wykonujemy, po prostu kładąc kartę na stole.
Zadanie Marcina, czyli odkrycie schowanej karty, jest prostsze. Wie, że piąta
karta jest takiego koloru jak pierwsza w kolejności. Wystarczy więc, że
odkoduje zakodowaną liczbę
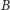 na podstawie permutacji ostatnich trzech
kart. Wtedy pójdzie o
na podstawie permutacji ostatnich trzech
kart. Wtedy pójdzie o
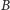 kart „w górę”, począwszy od pierwszej
w kolejności i już wie, jaka karta została ukryta.
kart „w górę”, począwszy od pierwszej
w kolejności i już wie, jaka karta została ukryta.
Przedstawię teraz, jak działa opisana sztuczka w konkretnym przypadku.
Załóżmy, że Karol dostał następujące karty:
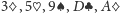 . Jak
widać, mamy dwie karty w kolorze karo (
. Jak
widać, mamy dwie karty w kolorze karo (
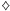 ), dlatego – zgodnie
z przyjętym algorytmem – którąś z nich będziemy kodować. Pomiędzy
trójką a asem jest
), dlatego – zgodnie
z przyjętym algorytmem – którąś z nich będziemy kodować. Pomiędzy
trójką a asem jest
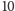 kart (
kart (
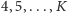 ), natomiast pomiędzy asem
a trójką tylko jedna (
), natomiast pomiędzy asem
a trójką tylko jedna (
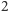 ). Dlatego to
). Dlatego to
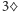 chowamy. Oczywiście,
najpierw kładziemy na stole asa karo, jako pierwszą kartę, następnie pozostałe
trzy sortujemy według rangi:
chowamy. Oczywiście,
najpierw kładziemy na stole asa karo, jako pierwszą kartę, następnie pozostałe
trzy sortujemy według rangi:
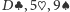 . Chcemy zakodować liczbę
. Chcemy zakodować liczbę
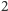 , ponieważ idąc od asa do trójki, trzeba zrobić dwa kroki (
, ponieważ idąc od asa do trójki, trzeba zrobić dwa kroki (
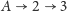 ). Dlatego najpierw kładziemy
). Dlatego najpierw kładziemy
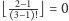 kartę,
czyli
kartę,
czyli
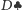 , następnie za pomocą kart
, następnie za pomocą kart
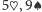 , kodujemy liczbę
, kodujemy liczbę
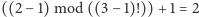 , czyli kładziemy następnie kartę
, czyli kładziemy następnie kartę
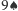 , no i na koniec pozostałą
, no i na koniec pozostałą
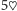 . Ostateczna kolejność to
. Ostateczna kolejność to
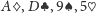 .
.
Otrzymawszy takie informacje, Marcin przystępuje do dzieła. Od razu wie, że
kolor poszukiwanej karty to
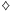 . Teraz pozostaje zdekodować liczbę
. Teraz pozostaje zdekodować liczbę
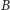 . Ponieważ jako pierwsza wśród kart kodujących permutację jest
najmniejsza z nich, więc poszukiwana liczba to
. Ponieważ jako pierwsza wśród kart kodujących permutację jest
najmniejsza z nich, więc poszukiwana liczba to
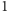 lub
lub
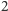 . Następnie
występuje starsza spośród pozostałych dwóch kart, więc szukana liczba to
. Następnie
występuje starsza spośród pozostałych dwóch kart, więc szukana liczba to
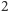 . Poczynając od pierwszej karty, czyli
. Poczynając od pierwszej karty, czyli
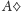 , odliczamy
, odliczamy
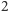 w górę i uzyskujemy wynik:
w górę i uzyskujemy wynik:
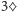 .
.
Znamy rozwiązanie, ale czy jest ono optymalne? Widzimy, że gdy więcej niż
dwie karty będą tego samego koloru, to w sposób dowolny wybieramy, którymi
dwiema z nich się zająć. Może dałoby się jeszcze więcej informacji
przekazać tym wyborem? Karol najpierw wybiera jedną kartę z pięciu,
potem wybiera jedną permutację z dwudziestu czterech, w sumie ma aż
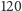 różnych sposobów ułożenia kart. Gdyby udało się w pełni
z tego bogactwa skorzystać, Marcin byłby w stanie odgadnąć jedną
ze
różnych sposobów ułożenia kart. Gdyby udało się w pełni
z tego bogactwa skorzystać, Marcin byłby w stanie odgadnąć jedną
ze
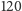 kart, więc cała talia mogłaby się składać ze
kart, więc cała talia mogłaby się składać ze
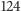 kart!
kart!
Przejdźmy do przypadku ogólnego. Przez
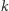 oznaczmy liczbę kart
losowanych z talii. Karol wybiera jedną z
oznaczmy liczbę kart
losowanych z talii. Karol wybiera jedną z
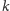 kart, potem jedną
z
kart, potem jedną
z
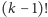 permutacji, w sumie ma
permutacji, w sumie ma
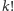 różnych możliwości, więc
niech nasza talia ma
różnych możliwości, więc
niech nasza talia ma
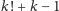 kart oznaczonych
kart oznaczonych
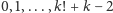 .
Oznaczmy wylosowane karty
.
Oznaczmy wylosowane karty
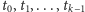 , tak by
, tak by
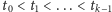 .
Niech
.
Niech
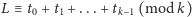 . Do odłożenia na bok wybieramy
kartę
. Do odłożenia na bok wybieramy
kartę
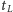 . Od teraz wszystkim kartom w talii, z pominięciem tych
. Od teraz wszystkim kartom w talii, z pominięciem tych
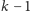 kart, jakie mamy na ręku, nadajemy w myślach nowe numery od
kart, jakie mamy na ręku, nadajemy w myślach nowe numery od
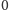 do
do
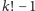 , tak by zachować kolejność. Nowy numer karty
, tak by zachować kolejność. Nowy numer karty
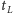 oznaczamy przez
oznaczamy przez
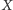 . Zauważmy, że dokładnie
. Zauważmy, że dokładnie
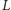 kart w naszym ręku ma numery mniejsze od
kart w naszym ręku ma numery mniejsze od
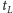 , więc podczas
przenumerowania karta
, więc podczas
przenumerowania karta
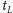 spadnie dokładnie o
spadnie dokładnie o
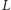 pozycji, wobec
czego
pozycji, wobec
czego
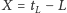 . Za pomocą ustalonego algorytmu permutowania tak
ustawiamy pozostałe na ręku karty, by kodowały
. Za pomocą ustalonego algorytmu permutowania tak
ustawiamy pozostałe na ręku karty, by kodowały
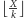 i pokazujemy je
Marcinowi.
i pokazujemy je
Marcinowi.
Marcin widzi wszystkie
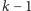 kart z naszej ręki, więc jest w stanie tak samo
jak my przenumerować wszystkie karty, których nie widzi. Ponadto zna
sumę
kart z naszej ręki, więc jest w stanie tak samo
jak my przenumerować wszystkie karty, których nie widzi. Ponadto zna
sumę
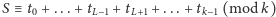 . Zauważmy, że
. Zauważmy, że
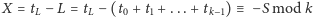 . Odkodowując liczbę
z permutacji, Marcin zna
. Odkodowując liczbę
z permutacji, Marcin zna
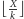 . Skoro
. Skoro
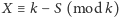 , to
, to
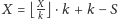 . Teraz już prosto, znając
. Teraz już prosto, znając
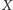 i karty na
naszym ręku, Marcin odwraca proces przenumerowywania i poznaje
i karty na
naszym ręku, Marcin odwraca proces przenumerowywania i poznaje
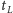 .
.
A dlaczego nie da się lepiej? Może ograniczenie
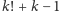 na liczebność
talii jest zbyt rygorystyczne? Postarajmy się to ściśle udowodnić. Ustalmy, że
talia składa się z
na liczebność
talii jest zbyt rygorystyczne? Postarajmy się to ściśle udowodnić. Ustalmy, że
talia składa się z
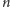 kart. Wtedy Karol jest postawiony wobec jednej
z
kart. Wtedy Karol jest postawiony wobec jednej
z
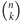 sytuacji, podejmuje swoje decyzje i przekazuje dane Marcinowi. Ten
może dostać od niego dokładnie
sytuacji, podejmuje swoje decyzje i przekazuje dane Marcinowi. Ten
może dostać od niego dokładnie
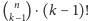 różnych układów
(
różnych układów
(
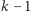 elementowe, uporządkowane podzbiory zbioru
elementowe, uporządkowane podzbiory zbioru
 elementowego). Przypuśćmy, że
elementowego). Przypuśćmy, że
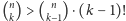 Wtedy, z zasady
szufladkowej Dirichleta, niezależnie od sposobu przyporządkowywania, będzie
istniał jakiś układ czterech kart, jakie Karol pokazał Marcinowi, któremu to
układowi odpowiada więcej niż jeden układ pięciu kart, jakie dostał na
początku Karol. Czyli nie każdy układ, jaki dostał na początku Karol, Marcin
będzie mógł jednoznacznie odtworzyć. Wobec czego, by sztuczka się
udała, musi być
Wtedy, z zasady
szufladkowej Dirichleta, niezależnie od sposobu przyporządkowywania, będzie
istniał jakiś układ czterech kart, jakie Karol pokazał Marcinowi, któremu to
układowi odpowiada więcej niż jeden układ pięciu kart, jakie dostał na
początku Karol. Czyli nie każdy układ, jaki dostał na początku Karol, Marcin
będzie mógł jednoznacznie odtworzyć. Wobec czego, by sztuczka się
udała, musi być
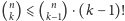 . Czyli
. Czyli
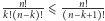 ,
zatem
,
zatem
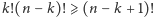 , co daje
, co daje
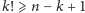 , więc
, więc
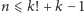 . Udowodniliśmy, że opisany powyżej schemat jest
optymalny.
. Udowodniliśmy, że opisany powyżej schemat jest
optymalny.
Sztuczkę tę wymyślił w latach dwudziestych XX wieku matematyk
amerykański Wiliam Fitch Chaney, Jr. (ur. 1894, zm. 1974). Już w dzieciństwie
interesował się sztuczkami magicznymi i ćwiczył swe zdolności manualne, by
zabawiać znajomych i rodzinę różnymi trickami. Później, gdy został
nauczycielem w Tufts College na początku lat dwudziestych, wykorzystywał swe
umiejętności, by zadziwić i zainteresować uczniów lekcją. Po raz
pierwszy jego sztuczka została opublikowana w książce Wallaca Lee
„Wallace Lee’s Magic Studio”. Od tego czasu pierwotna „five card trick”,
wykorzystująca zwykłą 52-kartową talię, doczekała się wielu odmian, począwszy
od omówionego rozszerzenia na talię 124-kartową, przez ogólny przypadek
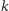 kart, wersję, gdy część kart może leżeć odwrócona, lub
możliwość chowania więcej niż jednej karty. Aby poznać więcej wersji,
polecam zapoznanie się z artykułem „Fitch Cheney’s Five Card Trick”
w Mathematical Association of America Math Horizons z lutego 2003
r.
kart, wersję, gdy część kart może leżeć odwrócona, lub
możliwość chowania więcej niż jednej karty. Aby poznać więcej wersji,
polecam zapoznanie się z artykułem „Fitch Cheney’s Five Card Trick”
w Mathematical Association of America Math Horizons z lutego 2003
r.