Toporna logika brudnych maszyn
Perpetuum mobile (z łac. "wiecznie poruszający się") pierwszego rodzaju to hipotetyczna maszyna, której jedynym efektem działania jest wykonywanie pracy, a więc również produkcja energii. Istnienie takiego tworu sprzeczne jest w oczywisty sposób z zasadą zachowania energii. Konstrukcją nieco bardziej wyrafinowaną jest perpetuum mobile drugiego rodzaju, a więc urządzenie, którego (jedynym) skutkiem funkcjonowania byłaby zamiana ciepła na pracę. Możliwość zbudowania takiej machiny nie jest bynajmniej wykluczona przez zasadę zachowania energii, a wizja urządzenia, które produkowałoby użyteczną pracę poprzez chłodzenie jakiegoś medium, może się (słusznie) wydać ze wszech miar pociągająca.
Historycznie jedno z pierwszych sformułowań drugiej zasady termodynamiki odwołuje się właśnie do tego poniekąd inżynieryjnego konceptu i pochodzi od Kelvina. Zasada Kelvina orzeka wprost, że perpetuum mobile drugiego rodzaju nie można zbudować. W rzeczy samej, pojęcie entropii w owych czasach nie istniało, ludzi zaś frapował (dziś nie mniej aktualny) problem maksymalnie efektywnego wykorzystania energii wyzwolonej wskutek spalenia czarnych substancji wykopywanych spod powierzchni ziemi. Z punktu widzenia języka współczesnych nauk przyrodniczych kelvinowskie sformułowanie fundamentalnego prawa fizyki (jakim jest druga zasada) poprzez odwołanie do brudnych i hałaśliwych maszyn cieplnych wydać się może nieco toporne. Podobnie sprawa wygląda z pochodzącym z równie zamierzchłych czasów sformułowaniem Clausiusa. Można z drugiej strony na ten problem spojrzeć jako na przykład ewolucji języka i tworzenia się (abstrakcyjnych poniekąd) pojęć inspirowanych przez, jak może się zdawać, ekstremalnie praktyczne zagadnienie, wskutek czego powstać może to, co nazywamy często "teorią fenomenologiczną".
Równoważna zasadzie Kelvina zasada Clausiusa orzeka, że niemożliwy jest proces, którego jedynym efektem byłby przepływ ciepła od ciała o temperaturze 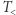 do ciała o wyższej temperaturze
do ciała o wyższej temperaturze 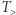 . Chronologicznie zasada Clausiusa (1850) nieznacznie poprzedza zasadę Kelvina i może być uznana za najwcześniejsze sformułowanie drugiej zasady termodynamiki. W pewnym sensie jej treść jest zawarta we wcześniejszej pracy Carnota (1824), która jednakże dotyczy "cieplika", czyli "fluidu ciepła", konceptu, który nie przetrwał próby czasu (tj. konfrontacji z doświadczeniem).
. Chronologicznie zasada Clausiusa (1850) nieznacznie poprzedza zasadę Kelvina i może być uznana za najwcześniejsze sformułowanie drugiej zasady termodynamiki. W pewnym sensie jej treść jest zawarta we wcześniejszej pracy Carnota (1824), która jednakże dotyczy "cieplika", czyli "fluidu ciepła", konceptu, który nie przetrwał próby czasu (tj. konfrontacji z doświadczeniem).
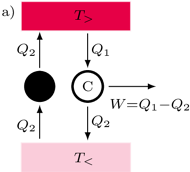
Rys. 1a
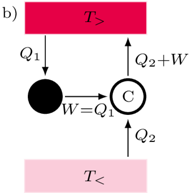
Rys. 1b
Zrozumienie równoważności zasad Kelvina 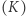 i Clausiusa
i Clausiusa 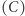 nie jest trudne. Obrazuje to diagram naszkicowany na rysunku 1 Ilustracja 1a pokazuje rozumowanie prowadzące do implikacji
nie jest trudne. Obrazuje to diagram naszkicowany na rysunku 1 Ilustracja 1a pokazuje rozumowanie prowadzące do implikacji 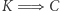 . Maszyna cieplna oznaczona jako kółko ze znakiem "C" pobiera ciepło
. Maszyna cieplna oznaczona jako kółko ze znakiem "C" pobiera ciepło 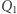 ze zbiornika o temperaturze
ze zbiornika o temperaturze 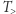 (grzejnika) i jego część oddaje do zbiornika o temperaturze
(grzejnika) i jego część oddaje do zbiornika o temperaturze 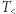 (chłodnicy), wykonując przy tym użyteczną pracę
(chłodnicy), wykonując przy tym użyteczną pracę 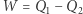 (na przykład służącą do rozpędzania lokomotywy). Rozumujemy teraz ad absurdum: zakładamy, że (wbrew zasadzie
(na przykład służącą do rozpędzania lokomotywy). Rozumujemy teraz ad absurdum: zakładamy, że (wbrew zasadzie 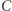 ) zbudowano machinę, której jedynym efektem działania jest przekaz ciepła od chłodnicy do grzejnika. Urządzenie to podłączamy tak, jak pokazuje rysunek 1a, gdzie oznaczone jest ono schematycznie czarnym kółkiem. Cały skonstruowany w ten sposób aparat de facto pobiera ciepło z grzejnika i zamienia na pracę. Jest to sprzeczne z zasadą
) zbudowano machinę, której jedynym efektem działania jest przekaz ciepła od chłodnicy do grzejnika. Urządzenie to podłączamy tak, jak pokazuje rysunek 1a, gdzie oznaczone jest ono schematycznie czarnym kółkiem. Cały skonstruowany w ten sposób aparat de facto pobiera ciepło z grzejnika i zamienia na pracę. Jest to sprzeczne z zasadą 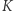 . W ten sposób pokazaliśmy implikację
. W ten sposób pokazaliśmy implikację 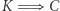 .
.
Dowód implikacji 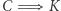 przebiega nieco podobnie. Zakładamy prawdziwość zasady
przebiega nieco podobnie. Zakładamy prawdziwość zasady 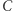 i znów uprawiamy reductio ad absurdum. Jeśli nasza teza (czyli zasada
i znów uprawiamy reductio ad absurdum. Jeśli nasza teza (czyli zasada 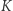 ) nie jest prawdziwa, to istnieje urządzenie przedstawione jako czarne koło na rysunku 1b. Posługując się maszyną C (działającą w odwróconym cyklu), zbudować możemy schemat z rysunku 1b, którego jedynym efektem działania jest przekazywanie ciepła od chłodnicy do grzejnika. Złamaliśmy zatem zasadę
) nie jest prawdziwa, to istnieje urządzenie przedstawione jako czarne koło na rysunku 1b. Posługując się maszyną C (działającą w odwróconym cyklu), zbudować możemy schemat z rysunku 1b, którego jedynym efektem działania jest przekazywanie ciepła od chłodnicy do grzejnika. Złamaliśmy zatem zasadę 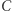 (wbrew założeniu, które na początku poczyniliśmy). Mamy zatem implikację
(wbrew założeniu, które na początku poczyniliśmy). Mamy zatem implikację 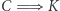 i w konsekwencji równoważność
i w konsekwencji równoważność 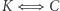 .
.
Wychodząc od zasady zachowania energii i zasady Kelvina (oraz konceptu empirycznej temperatury), zbudować można w gruncie rzeczy całą termodynamikę. Zobaczmy teraz, jak posługując się językiem maszyn, dotrzeć do drugiej zasady w ujęciu, które dziś można by uznać za standardowe. Przyda się do tego bardzo konkretne urządzenie, mianowicie znajomy silnik Carnota (działający w sposób odwracalny). Przypomnijmy, że urządzenie takie wymaga dwóch zbiorników cieplnych: grzejnika i chłodnicy, o temperaturach odpowiednio 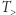 i
i 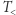 . Jego cykl składa się z czterech procesów:
. Jego cykl składa się z czterech procesów:
- (i)
- izotermicznego rozprężania w
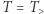 (czemu towarzyszy pobranie ciepła od grzejnika);
(czemu towarzyszy pobranie ciepła od grzejnika); - (ii)
- adiabatycznego rozprężania;
- (iii)
- izotermicznego sprężania w kontakcie z chłodnicą w
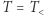 , któremu towarzyszy oddawanie ciepła do chłodnicy,
, któremu towarzyszy oddawanie ciepła do chłodnicy, - (iv)
- oraz adiabatycznego sprężania do osiągnięcia stanu wyjściowego. Zakładamy, że operacje te możemy również przeprowadzić w przeciwnym kierunku.
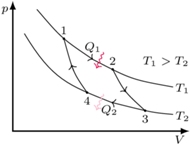
Rys. 2 Cykl Carnota na diagramie 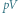 pokazującym zależność ciśnienia gazu od objętości:
pokazującym zależność ciśnienia gazu od objętości:
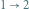 izotermiczne rozprężanie
izotermiczne rozprężanie
(układ pobiera ciepło),
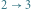 adiabatyczne rozprężanie
adiabatyczne rozprężanie
(układ wykonuje pracę),
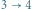 izotermiczne sprężanie
izotermiczne sprężanie
(układ oddaje ciepło),
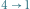 adiabatyczne sprężanie
adiabatyczne sprężanie
(praca jest wykonywana nad układem).
Całkowita praca, jaką w takim cyklu udaje się uzyskać z układu, jest równa polu obszaru ograniczonego krzywymi reprezentującymi cykl
Znana jest taka właściwość silnika Carnota, że stosunek ciepła pobranego 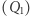 do ciepła oddanego
do ciepła oddanego 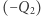 zależy jedynie od temperatur
zależy jedynie od temperatur 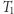 i
i 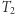 i wynosi
i wynosi 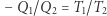 . Nadmienić można, że fakt ten służy do zdefiniowania temperatury absolutnej w fenomenologicznej konstrukcji termodynamiki (ale o tym może innym razem). Mamy więc dla rozpatrywanego silnika własność
. Nadmienić można, że fakt ten służy do zdefiniowania temperatury absolutnej w fenomenologicznej konstrukcji termodynamiki (ale o tym może innym razem). Mamy więc dla rozpatrywanego silnika własność 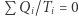 . Pokażemy teraz podobny wynik dla dowolnego cyklu odwracalnego oraz ważną nierówność przypisywaną Clausiusowi. Uprawiając konsekwentnie toporną logikę doskonale naoliwionych (funkcjonujących potencjalnie w sposób odwracalny) maszyn, rozpatrujemy dowolne urządzenie
. Pokażemy teraz podobny wynik dla dowolnego cyklu odwracalnego oraz ważną nierówność przypisywaną Clausiusowi. Uprawiając konsekwentnie toporną logikę doskonale naoliwionych (funkcjonujących potencjalnie w sposób odwracalny) maszyn, rozpatrujemy dowolne urządzenie 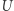 działające w sposób cykliczny. W każdym z "infinitezymalnych elementów" składających się na cykl praca jest wykonywana przez układ bądź nad układem i doprowadzane (bądź odprowadzane) jest ciepło. Wyobrażamy sobie teraz, że każdy element ciepła
działające w sposób cykliczny. W każdym z "infinitezymalnych elementów" składających się na cykl praca jest wykonywana przez układ bądź nad układem i doprowadzane (bądź odprowadzane) jest ciepło. Wyobrażamy sobie teraz, że każdy element ciepła 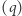 przekazywany jest do (bądź z) układu przez pomocniczy układ
przekazywany jest do (bądź z) układu przez pomocniczy układ 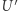 o temperaturze
o temperaturze 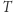 . Ponadto
. Ponadto 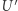 jest silnikiem Carnota mogącym działać pomiędzy temperaturą
jest silnikiem Carnota mogącym działać pomiędzy temperaturą 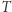 i (ustaloną) temperaturą zbiornika
i (ustaloną) temperaturą zbiornika 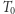 . Infinitezymalny element cyklu traktujemy więc jako następującą procedurę: (i)
. Infinitezymalny element cyklu traktujemy więc jako następującą procedurę: (i) 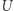 jest w danym stanie,
jest w danym stanie, 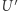 w stanie o temperaturze
w stanie o temperaturze 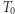 ; (ii) przeprowadzamy
; (ii) przeprowadzamy 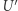 adiabatycznie (odwracalnie) do
adiabatycznie (odwracalnie) do 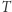 ; (iii)
; (iii) 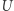 wykonuje element cyklu, absorbując ciepło
wykonuje element cyklu, absorbując ciepło 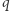 od
od 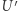 ,
, 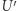 podąża wzdłuż izotermy odpowiadającej
podąża wzdłuż izotermy odpowiadającej 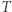 ; (iv)
; (iv) 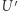 podlega adiabatycznej (odwracalnej) przemianie do temperatury
podlega adiabatycznej (odwracalnej) przemianie do temperatury 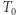 , a następnie jest sprężony (bądź rozprężony) do osiągnięcia stanu wyjściowego. Zauważamy teraz, że skoro w naszym infinitezymalnym procesie
, a następnie jest sprężony (bądź rozprężony) do osiągnięcia stanu wyjściowego. Zauważamy teraz, że skoro w naszym infinitezymalnym procesie 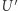 oddał w kroku (iii) ciepło
oddał w kroku (iii) ciepło 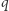 , to musi w kroku (iv) pobrać ciepło
, to musi w kroku (iv) pobrać ciepło 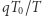 . W trakcie całego cyklu układu
. W trakcie całego cyklu układu 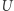 ciepło pobrane ze zbiornika wynosi zatem
ciepło pobrane ze zbiornika wynosi zatem 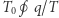 (gdzie całka przebiega po cyklu układu
(gdzie całka przebiega po cyklu układu 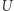 ). Zauważamy teraz, że po wykonaniu pełnego cyklu układy
). Zauważamy teraz, że po wykonaniu pełnego cyklu układy 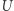 oraz
oraz 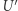 znalazły się w swoich stanach wyjściowych, a zatem ich energia (która jest funkcją stanu) nie zmieniła się. Ciepło
znalazły się w swoich stanach wyjściowych, a zatem ich energia (która jest funkcją stanu) nie zmieniła się. Ciepło 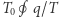 pobrane ze zbiornika musiało zatem zamienić się w pracę wykonaną w trakcie realizacji cyklu. Ale powołując się teraz na zasadę Kelvina, stwierdzamy, że nie może ono być dodatnie, a zatem
pobrane ze zbiornika musiało zatem zamienić się w pracę wykonaną w trakcie realizacji cyklu. Ale powołując się teraz na zasadę Kelvina, stwierdzamy, że nie może ono być dodatnie, a zatem
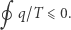 |
(1) |
Jest to słynna nierówność Clausiusa. Podkreślmy, że otrzymaliśmy ją, posługując się zasadą Kelvina i bardzo szczególną maszyną cieplną (odwracalnym silnikiem Carnota). Jeżeli dodatkowo cykl układu 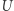 jest odwracalny, to powtarzając powyższe rozumowanie "w drugim kierunku" (biorąc
jest odwracalny, to powtarzając powyższe rozumowanie "w drugim kierunku" (biorąc 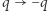 ), dostaniemy
), dostaniemy
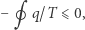 |
(2) |
co nieuchronnie prowadzi (dla cyklów odwracalnych) do równości
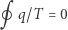 |
(3) |
i wniosku, że dla dowolnych dróg łączących stany 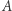 i
i 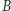 całka
całka 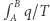 nie zależy od drogi. Możemy więc zdefiniować pewną funkcję
nie zależy od drogi. Możemy więc zdefiniować pewną funkcję 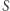 następującym wzorem:
następującym wzorem:
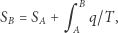 |
(4) |
gdzie 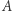 jest pewnym ustalonym stanem, dla którego wartość
jest pewnym ustalonym stanem, dla którego wartość 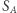 możemy przyjąć dowolnie. Wartość
możemy przyjąć dowolnie. Wartość 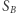 dla dowolnego innego stanu jest już jednoznacznie zadana powyższym wzorem, ponieważ całka nie zależy od drogi. Tak zdefiniowana funkcja
dla dowolnego innego stanu jest już jednoznacznie zadana powyższym wzorem, ponieważ całka nie zależy od drogi. Tak zdefiniowana funkcja 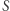 jest więc funkcją stanu (wyznaczoną z dokładnością do stałej, ze względu na dowolność wartości
jest więc funkcją stanu (wyznaczoną z dokładnością do stałej, ze względu na dowolność wartości 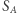 ). Konkluzję tę można też bardziej formalnie wyrazić następująco: z niezależności całki od drogi wynika, że forma
). Konkluzję tę można też bardziej formalnie wyrazić następująco: z niezależności całki od drogi wynika, że forma 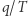 jest różniczką zupełną, a zatem istnieje funkcja stanu
jest różniczką zupełną, a zatem istnieje funkcja stanu 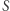 taka, że
taka, że 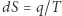 i dla dowolnych stanów
i dla dowolnych stanów 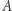 i
i 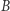 zachodzi równość (4).
zachodzi równość (4).
Co natomiast w sytuacji, gdy zarzucimy założenie odwracalności? Dla dowolnego procesu od 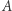 do
do 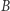 przeprowadzamy proces odwrotny w sposób odwracalny. Do otrzymanego w ten sposób cyklu stosujemy nierówność Clausiusa, co daje nam
przeprowadzamy proces odwrotny w sposób odwracalny. Do otrzymanego w ten sposób cyklu stosujemy nierówność Clausiusa, co daje nam 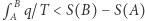 . W szczególności, gdy przeprowadzamy proces adiabatyczny (ale nieodwracalny), to
. W szczególności, gdy przeprowadzamy proces adiabatyczny (ale nieodwracalny), to 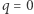 i
i 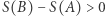 . Dla procesu infinitezymalnego mamy
. Dla procesu infinitezymalnego mamy 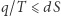 (gdzie równość zachodzi jedynie dla procesu odwracalnego).
(gdzie równość zachodzi jedynie dla procesu odwracalnego).
Nawiązaliśmy zatem kontakt z bardziej powszechnym podejściem do termodynamiki, gdzie istnienie funkcji 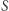 (zwanej entropią), określonej na stanach równowagi termodynamicznej jest postulatem. Niektóre kanoniczne podręczniki termodynamiki (np. książka A. Briana Pipparda z roku 1957) jako punkt startowy przyjmują właśnie zasadę Kelvina i wprowadzają entropię na podstawie rozumowania podanego (w nieco skróconej formie) powyżej. Wydaje się, że podejście to jest wypierane (bądź zostało wręcz wyparte) przez wzorzec logiczny oparty na książce Herberta Callena z roku 1966, gdzie termodynamika formułowana jest poprzez zasadę wariacyjną odnoszącą się do funkcji
(zwanej entropią), określonej na stanach równowagi termodynamicznej jest postulatem. Niektóre kanoniczne podręczniki termodynamiki (np. książka A. Briana Pipparda z roku 1957) jako punkt startowy przyjmują właśnie zasadę Kelvina i wprowadzają entropię na podstawie rozumowania podanego (w nieco skróconej formie) powyżej. Wydaje się, że podejście to jest wypierane (bądź zostało wręcz wyparte) przez wzorzec logiczny oparty na książce Herberta Callena z roku 1966, gdzie termodynamika formułowana jest poprzez zasadę wariacyjną odnoszącą się do funkcji 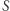 , której istnienie jest postulatem. Urok tego podejścia polega na tym, że termodynamika stanów równowagi w sposób jasny staje się zamkniętą teorią aksjomatyczną, opartą w gruncie rzeczy na zasadzie zachowania energii oraz pewnej eleganckiej (choć być może lekko enigmatycznej) zasadzie wariacyjnej, której sensowność weryfikowana jest de facto a posteriori. Odrobinę kuriozalnym jest fakt, że w tej wersji kursu termodynamiki poradzić można sobie bez odwołania się do maszyn cieplnych, zasady Kelvina i Clausiusa natomiast pominąć, bądź też przywołać jako "historyczne" sformułowania II zasady (co słuchaczom wyda się zapewne cokolwiek nudną i nie do końca potrzebną dygresją). Urzekająca w swej estetyce aksjomatyczna termodynamika jest "ortogonalna" do historycznej logiki brudnych maszyn. Logika brudnych maszyn jest natomiast czysta, acz może nieco toporna.
, której istnienie jest postulatem. Urok tego podejścia polega na tym, że termodynamika stanów równowagi w sposób jasny staje się zamkniętą teorią aksjomatyczną, opartą w gruncie rzeczy na zasadzie zachowania energii oraz pewnej eleganckiej (choć być może lekko enigmatycznej) zasadzie wariacyjnej, której sensowność weryfikowana jest de facto a posteriori. Odrobinę kuriozalnym jest fakt, że w tej wersji kursu termodynamiki poradzić można sobie bez odwołania się do maszyn cieplnych, zasady Kelvina i Clausiusa natomiast pominąć, bądź też przywołać jako "historyczne" sformułowania II zasady (co słuchaczom wyda się zapewne cokolwiek nudną i nie do końca potrzebną dygresją). Urzekająca w swej estetyce aksjomatyczna termodynamika jest "ortogonalna" do historycznej logiki brudnych maszyn. Logika brudnych maszyn jest natomiast czysta, acz może nieco toporna.
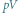 pokazującym zależność ciśnienia gazu od objętości:
pokazującym zależność ciśnienia gazu od objętości: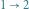 izotermiczne rozprężanie
izotermiczne rozprężanie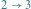 adiabatyczne rozprężanie
adiabatyczne rozprężanie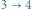 izotermiczne sprężanie
izotermiczne sprężanie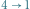 adiabatyczne sprężanie
adiabatyczne sprężanie