Klub 44F - zadania IX 2017»Zadanie 642
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania IX 2017
- Publikacja w Delcie: wrzesień 2017
- Publikacja elektroniczna: 1 września 2017
- Artykuł źródłowy w wersji do druku [application/pdf]: (111 KB)

Piłka o promieniu 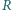 słabo uderza w ścianę i deformuje się, jak pokazano na rysunku. Deformacja
słabo uderza w ścianę i deformuje się, jak pokazano na rysunku. Deformacja 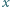 jest dużo mniejsza od promienia piłki i możemy przyjąć, że ciśnienie powietrza w piłce nie zmienia się podczas uderzenia. Zaniedbując sprężystość powłoki, oszacować czas zderzenia piłki ze ścianą. Masa piłki wynosi
jest dużo mniejsza od promienia piłki i możemy przyjąć, że ciśnienie powietrza w piłce nie zmienia się podczas uderzenia. Zaniedbując sprężystość powłoki, oszacować czas zderzenia piłki ze ścianą. Masa piłki wynosi 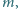 ciśnienie powietrza w piłce
ciśnienie powietrza w piłce 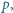 ciśnienie atmosferyczne
ciśnienie atmosferyczne 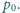


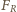 oraz siła
oraz siła 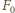 spowodowana ciśnieniem atmosferycznym. Zgodnie z trzecią zasadą dynamiki siła reakcji równa jest co do wartości sile nacisku piłki na ścianę. Ponieważ możemy zaniedbać sprężystość powłoki, więc
spowodowana ciśnieniem atmosferycznym. Zgodnie z trzecią zasadą dynamiki siła reakcji równa jest co do wartości sile nacisku piłki na ścianę. Ponieważ możemy zaniedbać sprężystość powłoki, więc 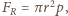 gdzie
gdzie  jest promieniem powierzchni zetknięcia piłki ze ścianą (rysunek). W celu znalezienia siły
jest promieniem powierzchni zetknięcia piłki ze ścianą (rysunek). W celu znalezienia siły 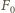 podzielmy myślowo powierzchnię piłki stykającą się z powietrzem na małe elementy o powierzchni
podzielmy myślowo powierzchnię piłki stykającą się z powietrzem na małe elementy o powierzchni 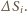 Na każdy element działa prostopadle do niego siła
Na każdy element działa prostopadle do niego siła 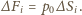 Wobec symetrii składowe równoległe do ściany wszystkich tych sił znoszą się, siła
Wobec symetrii składowe równoległe do ściany wszystkich tych sił znoszą się, siła 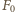 skierowana jest prostopadle w kierunku ściany i ma wartość
skierowana jest prostopadle w kierunku ściany i ma wartość 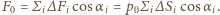 Z
Z 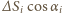 jest rzutem
jest rzutem 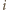 -tego elementu powierzchni na płaszczyznę pionową, a suma tych wielkości równa jest powierzchni styku piłki ze ścianą. Stąd
-tego elementu powierzchni na płaszczyznę pionową, a suma tych wielkości równa jest powierzchni styku piłki ze ścianą. Stąd 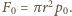 Wypadkowa siła działająca na piłkę wynosi zatem
Wypadkowa siła działająca na piłkę wynosi zatem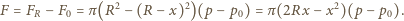
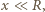 mamy
mamy 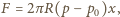 a zwrot
a zwrot 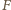 jest przeciwny do deformacji
jest przeciwny do deformacji 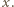 W rozważanym przybliżeniu piłka podczas zderzenia ze ścianą porusza się ruchem harmonicznym z okresem
W rozważanym przybliżeniu piłka podczas zderzenia ze ścianą porusza się ruchem harmonicznym z okresem 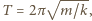 gdzie
gdzie 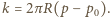 Czas zderzenia piłki ze ścianą równy jest połowie okresu:
Czas zderzenia piłki ze ścianą równy jest połowie okresu: