Zadanie ZF-867
o zadaniu...
- Publikacja w Delcie: listopad 2014
- Publikacja elektroniczna: 31-10-2014
Otwarte akwarium w kształcie półsfery o średnicy 30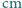 
wypełniono całkowicie wodą i umieszczono w pokoju, w którym nie ma prądów powietrza. Przez dwie doby poziom wody w akwarium obniżył się o 1 centymetr. Przyjmując, że temperatura i wilgotność powietrza w pokoju są stałe, a proces parowania jest na tyle powolny, że temperatura wody nie ulega zmianie, znaleźć czas, po którym woda całkowicie wyparuje z akwarium.
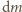parująca w bardzo krótkim czasie 
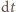jest proporcjonalna do pola powierzchni wody 
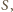czyli 
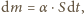gdzie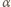 
jest współczynnikiem proporcjonalności. Zmiana poziomu wody w akwarium 
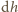wiąże się ze zmianą jej masy zależnością 
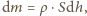gdzie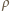 
- gęstość wody. Stąd 
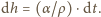Tak więc w stałych warunkach parowania zmiana poziomu wody jest proporcjonalna do czasu. Jeżeli więc przez dwie doby poziom wody obniżył się o 1 centymetr, to cała woda, przy głębokości akwarium równej 15 
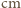, wyparuje po 30 dobach.