Klub 44F - zadania III 2017»Zadanie 634
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania III 2017
- Publikacja w Delcie: marzec 2017
- Publikacja elektroniczna: 1 marca 2017
- Artykuł źródłowy w wersji do druku [application/pdf]: (83 KB)

W pionowym, zamkniętym naczyniu znajduje się tłok, który może przemieszczać się bez tarcia. Z obu stron tłoka znajdują się jednakowe masy tego samego gazu doskonałego. W temperaturze 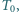 jednakowej w całym naczyniu, objętość gazu nad tłokiem jest
jednakowej w całym naczyniu, objętość gazu nad tłokiem jest 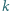 razy większa niż objętość gazu pod tłokiem. Jaki będzie stosunek tych objętości, gdy temperatura wzrośnie do wartości
razy większa niż objętość gazu pod tłokiem. Jaki będzie stosunek tych objętości, gdy temperatura wzrośnie do wartości 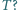

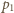 i
i 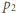 ciśnienia w dolnej i górnej części naczynia w temperaturze
ciśnienia w dolnej i górnej części naczynia w temperaturze 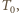 a przez
a przez 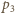 i
i 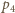 odpowiednie ciśnienia w temperaturze
odpowiednie ciśnienia w temperaturze 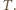 Różnica ciśnień związana jest z ciężarem tłoka i nie zależy od temperatury
Różnica ciśnień związana jest z ciężarem tłoka i nie zależy od temperatury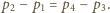
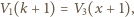
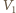 i
i 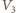 to początkowa i końcowa objętość gazu w dolnej części naczynia, a
to początkowa i końcowa objętość gazu w dolnej części naczynia, a  jest szukanym stosunkiem objętości w stanie końcowym. Masy gazu w obu częściach naczynia są takie same, z równań Clapeyrona wynikają więc związki
jest szukanym stosunkiem objętości w stanie końcowym. Masy gazu w obu częściach naczynia są takie same, z równań Clapeyrona wynikają więc związki 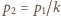 oraz
oraz 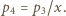 Podstawiając je do równania (1), otrzymujemy
Podstawiając je do równania (1), otrzymujemy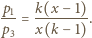
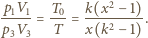
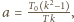 możemy napisać równanie kwadratowe na szukaną wielkość
możemy napisać równanie kwadratowe na szukaną wielkość 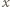 w postaci
w postaci 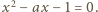 Dodatni pierwiastek tego równania ma postać
Dodatni pierwiastek tego równania ma postać 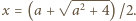 Dla
Dla 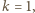 co odpowiada nieważkiemu tłokowi,
co odpowiada nieważkiemu tłokowi, 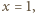 czyli objętości gazów nad i pod tłokiem są takie same. Dla dowolnego
czyli objętości gazów nad i pod tłokiem są takie same. Dla dowolnego 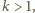 gdy temperatura dąży do nieskończoności, wartość
gdy temperatura dąży do nieskończoności, wartość 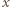 również dąży do 1. W bardzo wysokiej temperaturze ciśnienia gazów w obu częściach naczynia są na tyle duże, że wpływ siły ciężkości tłoka można pominąć.
również dąży do 1. W bardzo wysokiej temperaturze ciśnienia gazów w obu częściach naczynia są na tyle duże, że wpływ siły ciężkości tłoka można pominąć.