Lodowa maszyna cieplna
Znane powiedzenie mówi, że istnieją dwie szkoły: otwocka oraz falenicka. Jedna na pewno jest lepsza, druga oczywiście gorsza; sęk w tym, że nie wiadomo, która jest jaka.

Nie inaczej bywa i w fizyce. Można podać wiele przykładów, choćby termodynamikę. Jedni są zafascynowani jej formalizmem matematycznym (czytaj - formami różniczkowymi), drudzy bardziej zachwycają się fizyczną treścią i pomysłowością dowodów korzystających z własności cykli Carnota. Ten artykuł traktuje o specyficznym cyklu Carnota i jeśli jest deklaracją przynależności autora do jakiejś szkoły, to niechybnie będzie nią szkoła z Glasgow. (Jak zatem będzie brzmiał właściwy przymiotnik?)
Z doświadczenia wiemy, że zamarzająca woda zwiększa swoją objętość. Dlatego czasami pękają źle zabezpieczone rury, a w górach woda zamarzająca w skalnych szczelinach kruszy najmocniejsze nawet skały, przyspieszając procesy erozji. Wykorzystamy fakt zmiany objętości cieczy podczas przemiany fazowej do ataku na drugą zasadę termodynamiki, by potem (niczym strażak, który podpala, żeby gasić) dzielnie ją obronić. Zbudujmy zatem cykl pokazany na rysunku na następnej stronie; nazwiemy ów cykl lodową maszyną cieplną.
Cylinder zamknięty ruchomym tłokiem (jak zwykle w tego rodzaju dyskusjach przyjmujemy, że tłok porusza się bez tarcia) wypełniony jest wodą o temperaturze równej temperaturze krzepnięcia. Na zewnątrz tłoka znajduje się powietrze o normalnym ciśnieniu atmosferycznym. Na tłoku (A) stawiamy ciało o masie 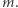 Układ znajduje się w jednorodnym polu grawitacyjnym o natężeniu
Układ znajduje się w jednorodnym polu grawitacyjnym o natężeniu 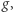 a więc aby podnieść ciało, należy wykonać pracę. Następnie w temperaturze krzepnięcia odbieramy od wody ciepło. Woda zamarza, zwiększa objętość i podnosi ciało znajdujące się na tłoku (B). Następnie (C) zsuwamy ciało z tłoka (praca związana z poziomym przesuwaniem tego ciała może być dowolnie mała). Na końcu dostarczamy do lodu ciepło, tak by go stopić, temperatura jest w tym procesie stała. Po stopieniu lodu układ znajduje się w stanie początkowym (D), natomiast masa
a więc aby podnieść ciało, należy wykonać pracę. Następnie w temperaturze krzepnięcia odbieramy od wody ciepło. Woda zamarza, zwiększa objętość i podnosi ciało znajdujące się na tłoku (B). Następnie (C) zsuwamy ciało z tłoka (praca związana z poziomym przesuwaniem tego ciała może być dowolnie mała). Na końcu dostarczamy do lodu ciepło, tak by go stopić, temperatura jest w tym procesie stała. Po stopieniu lodu układ znajduje się w stanie początkowym (D), natomiast masa 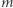 została podniesiona na wyższy poziom.
została podniesiona na wyższy poziom.
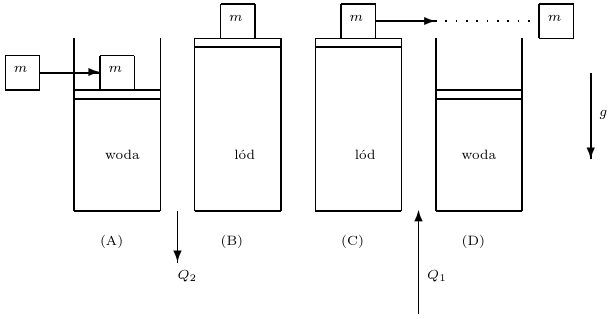
Lodowy silnik cieplny. Zgodnie z pierwszą zasadą termodynamiki praca wykorzystana do podniesienia masy 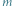 jest równa różnicy ciepeł:
jest równa różnicy ciepeł: 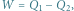 gdzie
gdzie 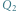 jest ciepłem wydzielającym się w trakcie zamarzania wody, a
jest ciepłem wydzielającym się w trakcie zamarzania wody, a 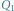 jest ciepłem zużytym do stopienia lodu. Przyjmujemy, że układ jest na tyle mały, że możemy zaniedbać niejednorodność ciśnienia w zbiorniku
jest ciepłem zużytym do stopienia lodu. Przyjmujemy, że układ jest na tyle mały, że możemy zaniedbać niejednorodność ciśnienia w zbiorniku
I tak oto natrafiamy na bardzo poważny kłopot. Wymiana ciepła pomiędzy wodą i otoczeniem oraz pomiędzy lodem i otoczeniem zachodzi w temperaturze 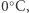 bo taka jest temperatura krzepnięcia wody i topnienia lodu. Efektywnie pobrane ciepło (czyli różnica ciepła pobranego przy topnieniu lodu i oddanego przy zamrażaniu wody) zostaje w całości zamieniona na pracę. Jest to sprzeczne z drugą zasadą termodynamiki w sformułowaniu Kelvina!
bo taka jest temperatura krzepnięcia wody i topnienia lodu. Efektywnie pobrane ciepło (czyli różnica ciepła pobranego przy topnieniu lodu i oddanego przy zamrażaniu wody) zostaje w całości zamieniona na pracę. Jest to sprzeczne z drugą zasadą termodynamiki w sformułowaniu Kelvina!
Problem ten rozwiązał brat lorda Kelvina, James Thomson, profesor mechaniki inżynieryjnej na Uniwersytecie w Glasgow (lord Kelvin był profesorem fizyki tego Uniwersytetu). Proces zamarzania i proces topnienia przebiegają w innych warunkach. Ze względu na obecność masy 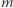 zamarzanie zachodzi przy wyższym ciśnieniu niż topnienie, kiedy na tłoku nie stoi już masa
zamarzanie zachodzi przy wyższym ciśnieniu niż topnienie, kiedy na tłoku nie stoi już masa 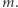 Jeśli słuszna jest druga zasada termodynamiki, to oba procesy muszą zachodzić w innej temperaturze. A to oznacza, że temperatura topnienia lodu zależy od jego ciśnienia. Ciało robocze (czyli woda/lód) musi wymieniać ciepło z dwoma termostatami. Pobierać ciepło od termostatu o wyższej temperaturze (topnienie lodu pod niższym ciśnieniem) i oddawać ciepło do termostatu o niższej temperaturze (zamarzanie wody przy podwyższonym ciśnieniu). Tak więc funkcja
Jeśli słuszna jest druga zasada termodynamiki, to oba procesy muszą zachodzić w innej temperaturze. A to oznacza, że temperatura topnienia lodu zależy od jego ciśnienia. Ciało robocze (czyli woda/lód) musi wymieniać ciepło z dwoma termostatami. Pobierać ciepło od termostatu o wyższej temperaturze (topnienie lodu pod niższym ciśnieniem) i oddawać ciepło do termostatu o niższej temperaturze (zamarzanie wody przy podwyższonym ciśnieniu). Tak więc funkcja 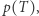 czyli ciśnienie w funkcji temperatury dla współistnienia wody i lodu jest funkcją malejącą. Jest to fakt potwierdzony doświadczalnie.
czyli ciśnienie w funkcji temperatury dla współistnienia wody i lodu jest funkcją malejącą. Jest to fakt potwierdzony doświadczalnie.
Być może dziś wydaje nam się to trywialne, ale w tamtych czasach choć wiedziano o wpływie ciśnienia na temperaturę wrzenia, jednak nie wiedziano, że wpływa też na temperaturę topnienia. Czyż nie jest zatem piękne, że z faktu zmiany objętości substancji w trakcie przemiany fazowej - na podstawie drugiej zasady termodynamiki w jej historycznym, kelwinowskim sformułowaniu - potrafimy wyprowadzić istnienie związku pomiędzy temperaturą przemiany fazowej a ciśnieniem? Przysłowie mówi, że wszystkie drogi prowadzą do Rzymu. Termodynamicznym Rzymem jest Druga Zasada.
Zauważmy jeszcze jedną rzecz. W sytuacji, w której ciepło jest pobierane przez otoczenie przy innym ciśnieniu i temperaturze niż wtedy, gdy jest od otoczenia odbierane, musimy dwie izotermy połączyć dwiema adiabatami (a zatem otrzymujemy prawdziwy cykl Carnota), które nie były potrzebne w pierwszej, naiwnej (jednoizotermowej) wersji lodowego silnika cieplnego.
W powyższym rozumowaniu pominęliśmy zjawisko ściśliwości i wody, i lodu. Nie jest to jednak bardzo wielki grzech, jeśli tylko masa 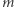 nie jest zbyt duża. Zmiana objętości wywołana dodatkowym ciśnieniem pochodzącym od ciężaru ciała
nie jest zbyt duża. Zmiana objętości wywołana dodatkowym ciśnieniem pochodzącym od ciężaru ciała 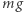 jest nieznaczna w porównaniu ze zmianą objętości podczas przemiany fazowej.
jest nieznaczna w porównaniu ze zmianą objętości podczas przemiany fazowej.
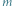 jest równa różnicy ciepeł:
jest równa różnicy ciepeł: 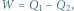 gdzie
gdzie 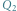 jest ciepłem wydzielającym się w trakcie zamarzania wody, a
jest ciepłem wydzielającym się w trakcie zamarzania wody, a 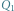 jest ciepłem zużytym do stopienia lodu. Przyjmujemy, że układ jest na tyle mały, że możemy zaniedbać niejednorodność ciśnienia w zbiorniku
jest ciepłem zużytym do stopienia lodu. Przyjmujemy, że układ jest na tyle mały, że możemy zaniedbać niejednorodność ciśnienia w zbiorniku