Intrygującym zagadnieniem jest powiązanie nieodwracalnych procesów, którym podlegają makroskopowe układy (i o których mówi druga zasada), z równaniami ewolucji czasowej (na przykład równaniami Newtona), które nie wyróżniają kierunku czasu. W badaniu tego problemu i zrozumieniu związanych z nim "paradoksów" kluczową rolę odgrywa statystyczny charakter drugiej zasady. Czy można więc "na palcach" pokazać nieuchronny wzrost entropii i nieodwracalność? (O strzałce czasu pisał Piotr Szymczak w Delta 01/2019.) Rozpatrzmy izolowany układ wielu 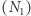cząstek o ustalonej całkowitej energii 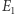(oraz innych parametrach, takich jak objętość). Na poziomie mikroskopowym taki stan realizowany może być na wiele 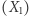sposobów (na przykład poszczególnym cząstkom mogą być przypisane różne wartości energii, z jedynym warunkiem, aby ich suma wynosiła 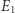). Zakładamy tu, że 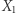jest jednoznaczną funkcją 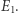Przyjmijmy za "daną" definicję entropii 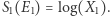Taka definicja gwarantuje, że całkowita entropia niezależnych układów jest równa sumie tychże entropii. To dlatego, że Oczywiście, logarytm jest funkcją rosnącą, zatem duża ilość dostępnych stanów mikroskopowych oznacza dużą entropię. 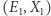Rozpatrzmy teraz dwa takie układy, scharakteryzowane odpowiednio przez oraz 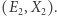Doprowadzając je do kontaktu, pozwalamy na wymianę energii przy warunku zachowania jej całkowitej wartości: 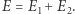Całkowita liczba dostępnych stanów mikroskopowych wyniesie teraz

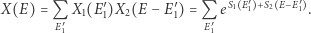(1)

Wynika stąd, że 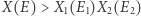(ponieważ 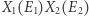jest jednym ze składników sumy), a więc entropia wzrosła. W sytuacji, gdy liczba cząstek w układzie jest odpowiednio duża, wyrażenie po prawej stronie jest zdominowane przez największy z wyrazów go tworzących (odpowiadający maksimum wyrażenia w wykładniku). Dostajemy wówczas

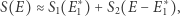(2)

gdzie 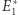odpowiada maksimum wyrażenia po prawej stronie powyższego równania. Ukazuje to drugą zasadę jako zasadę ekstremum: gdy dwa układy doprowadzimy do kontaktu, pozwalając na ich oddziaływanie, nowy stan równowagi będzie taki, by entropia osiągała maksymalną możliwą wartość. Wybierając (losowo) jeden spośród 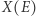stanów, mamy oczywiście pewną szansę, że trafimy na przypadek, gdzie 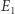istotnie różni się od 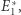ale dla dużej liczby cząstek 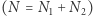prawdopodobieństwo takiego trafu jest znikomo małe. Dzieje się tak dlatego, że przybliżenie, którego użyliśmy, pisząc wzór (2) i wybierając tylko wiodący wyraz w równaniu (1), jest tym lepsze, im większa wartość wykładnika, który z kolei jest rzędu 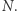Dla typowo spotykanych wartości 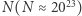przybliżenie zastosowane w wyrażeniu (2) jest z praktycznego punktu widzenia niezwykle dokładne. Zauważyć można, że powyższe spojrzenie w ogóle nie rozpatruje ewolucji układu. Przyjmuje jedynie, że przy pomiarze stanu układu dostajemy z równymi (albo zbliżonymi) prawdopodobieństwami różne wyniki. W ujęciu, w którym śledzimy ewolucję układu, stwierdzilibyśmy, że układ niezależnie od stanu początkowego spędza przytłaczającą większość czasu w stanach odpowiadających maksimum entropii (czyli takich, że ).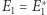