Aktualności (nie tylko) fizyczne
Pod prąd
Dożyliśmy czasów, w których ustawicznie należy podnosić swoje kompetencje, żeby nie pozostać w tyle. Pod prąd temu poglądowi chciałbym pokazać, jak przerost wiedzy może uniemożliwić dostrzeżenie prostego rozwiązania zadania z olimpiady fizycznej z roku 1980 o następującej treści...
Zadanie. Do jakiej maksymalnej temperatury można ogrzać litr czystej
wody
o temperaturze
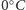 za pomocą litra brudnej wody o temperaturze
za pomocą litra brudnej wody o temperaturze
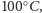 dysponując naczyniami o dowolnych kształtach i objętości,
o ściankach idealnie izolujących lub idealnie przewodzących ciepło?
dysponując naczyniami o dowolnych kształtach i objętości,
o ściankach idealnie izolujących lub idealnie przewodzących ciepło?
Rozwiązanie można napisać od razu i to jednym zdaniem (jest ono podane na dole strony). Pomimo to chyba nikomu z olimpijczyków nie udało się udzielić poprawnej odpowiedzi.
Dużo było powołań na II zasadę termodynamiki, z której miałoby wynikać,
że taką temperaturą jest
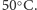 Wystarczy jednak rozlać czystą wodę
do dwóch półlitrówek i ogrzać je kolejno brudną wodą, żeby uzyskać
(po zmieszaniu) temperaturę
Wystarczy jednak rozlać czystą wodę
do dwóch półlitrówek i ogrzać je kolejno brudną wodą, żeby uzyskać
(po zmieszaniu) temperaturę
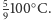 Jak widać, sama wiedza
o istnieniu II zasady termodynamiki nie pomaga. Wprost przeciwnie.
Jak widać, sama wiedza
o istnieniu II zasady termodynamiki nie pomaga. Wprost przeciwnie.
Żeby rozwiązać zadanie, należy wymyślić, jak wodę podzielić, żeby uzyskać jak najlepszy efekt. Łatwo przekonać się, że należy porcjować również brudną wodę. Efektywna jest zasada przeciwprądu. Można ją zilustrować następująco. Podzielmy każdą z wód np. na ćwiartki i ustawmy z nich przeciwbieżne pociągi. Najpierw zetkniemy butelki pierwsza z pierwszą. Po wyrównaniu temperatur przesuwamy pociągi o jedną butelkę. Wtedy pierwsza czysta zetknie się z drugą brudną oraz druga czysta z pierwszą brudną. Temperaturę zetkniętych butelek (po jej ustaleniu się w każdym kroku) oraz butelek, które mają się zetknąć w następnym kroku (lub ostatni raz były zetknięte w poprzednim), można przedstawić za pomocą poniższego schematu (liczby trzeba pomnożyć przez 100, żeby otrzymać temperaturę w skali Celsjusza).

Wiersze przedstawiają kolejne etapy. W nawiasach kwadratowych jest woda brudna, natomiast w zwykłych czysta. Bez nawiasów przedstawiono temperaturę zetkniętych butelek. Oczywiście, każda liczba bez nawiasu jest średnią arytmetyczną dwóch liczb powyżej (można też sumować parami osobno mianowniki i osobno liczniki).
Po zlaniu osobno czystej oraz osobno brudnej wody (obliczeniu średniej
ułamków w nawiasach zwykłych oraz kwadratowych umieszczonych na dole
schematu) otrzymujemy temperatury, odpowiednio,
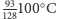 oraz
oraz
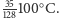 Przy początkowym podziale na półlitrówki otrzymalibyśmy
Przy początkowym podziale na półlitrówki otrzymalibyśmy
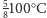 oraz
oraz
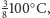 natomiast po rozlaniu każdej z wód
do ośmiu butelek uzyskalibyśmy
natomiast po rozlaniu każdej z wód
do ośmiu butelek uzyskalibyśmy
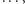 no właśnie ile? Czy warto ten
żmudny rachunek wykonywać? Chyba że jako wprawkę z programowania.
A i tak trzeba by było obliczyć granicę przy rosnącej do nieskończoności
krotności podziału. Nawet gdyby się udało (nie jestem wcale pewien, czy jest to
wykonalne, może jest to jakieś wyzwanie?), to jak udowodnić, że nie ma
jeszcze lepszego sposobu?
no właśnie ile? Czy warto ten
żmudny rachunek wykonywać? Chyba że jako wprawkę z programowania.
A i tak trzeba by było obliczyć granicę przy rosnącej do nieskończoności
krotności podziału. Nawet gdyby się udało (nie jestem wcale pewien, czy jest to
wykonalne, może jest to jakieś wyzwanie?), to jak udowodnić, że nie ma
jeszcze lepszego sposobu?
Rozterki te biorą się jednak wyłącznie z faktu dysponowania pojęciem granicy. Ale dla większości współczesnych maturzystów ta wiedza jest hermetyczna. I bardzo dobrze, bo nie o to tu chodzi. Pamiętajmy, że jest to uproszczony, ale jednak fizyczny problem. Właściwie jest to zadanie inżynierskie (i takie jest proste rozwiązanie zamieszczone na końcu).
Okazuje się, że jest lepszy sposób, będący banalną (choć istotną) modyfikacją już przedstawionego rozwiązania.
Nie musimy naraz używać całej objętości wody w procesie przekazywania
energii. Moglibyśmy nadal używać czterech pojemników, ale np. o połowę
mniejszej objętości. Po wykorzystaniu każdy pojemnik opróżniamy
do naczynia, w którym ma się znaleźć czysta woda po ogrzaniu,
a w kolejnym kroku (po napełnieniu nieogrzaną czystą wodą) przenosimy go
na koniec pociągu (analogicznie postępujemy z brudną wodą). Wtedy uzyskamy
taki sam końcowy rozkład temperatury, ale tylko dla połowy objętości,
a druga połowa, (znajdująca się już w naczyniach odbiorczych) będzie miała
temperatury
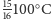 dla czystej oraz
dla czystej oraz
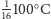 dla brudnej wody.
Po zlaniu całej wody każdego rodzaju do naczyń odbiorczych wynik będzie
trochę gorszy:
dla brudnej wody.
Po zlaniu całej wody każdego rodzaju do naczyń odbiorczych wynik będzie
trochę gorszy:
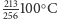 oraz
oraz
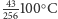 .
.
Temperatury wody wlewanej do naczyń odbiorczych można dowolnie zbliżyć do początkowych temperatur drugiego rodzaju wody, zwiększając liczbę pojemników. Natomiast pogorszenie wyniku, ze względu na konieczność dolania wody pozostałej w pociągach, można zniwelować poprzez zminimalizowanie objętości pojemników. W ten sposób uzyskujemy dowolnie dokładną wzajemną zamianę temperatur dwóch używanych rodzajów wody.
Dlaczego to zadanie sprawia trudności?
Bo nie jest standardowe. W takim przypadku istotna jest tylko świadomość, co jest (dla mnie) niemożliwe, lub odkrycie, co trzeba odrzucić, żeby niemożliwe takim być przestało. To jest właściwa miara naszych kompetencji.