W pół drogi do nieskończoności
W termodynamice charakteryzujemy równowagowy układ za pomocą pewnego zbioru parametrów (np. ciśnienia, objętości i temperatury) i związków pomiędzy nimi (np. równania stanu gazu). Wielkości te są funkcjami stanu, a więc są jednoznacznie przyporządkowane danemu stanowi układu i nie zmieniają się w czasie. Jeśli jednak spojrzymy na układ z punktu widzenia jego struktury mikroskopowej, na cząsteczki gazu w ciągłym ruchu, powstaje pytanie: jak powiązać charakterystyki termodynamiczne układu z jego mikroskopową dynamiką?
Chmura składa się z obłoków złożonych z obłoków,
które składają się obłoków,
które wyglądają jak chmury.
Ale kiedy zbliżasz się do chmury,
nie widzisz gładkości,
tylko nieregularności w drobniejszej skali
Benoît Mandelbrot (1924–2010)
Odpowiedzi na to pytanie udziela mechanika statystyczna, w myśl której układ wielu cząsteczek podlega prawom statystycznym, a parametry makroskopowe są średnimi wartościami odpowiednich wyrażeń mikroskopowych. Przykładowo, średnia energia kinetyczna cząsteczek gazu doskonałego, w którym prędkości cząsteczek opisane są rozkładem Maxwella, jest powiązana z temperaturą gazu poprzez relację
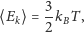 | (1) |
gdzie
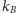 jest stałą Boltzmanna. W naturalny sposób w grze pojawia się
więc pojęcie prawdopodobieństwa. Ze względu na statystyczną naturę
opisywanych zagadnień w skończonym układzie parametry termodynamiczne
podlegają zmianom w czasie, przyjmując wartości zbliżone do średniej.
Zmiany te nazywamy fluktuacjami. Oszacowanie wielkości fluktuacji jest
równoznaczne z badaniem odpowiedniego rozkładu prawdopodobieństwa.
Dopiero gdy dysponujemy oszacowaniem wartości średniej i średnim
odchyleniem od tej wartości, jesteśmy w stanie zinterpretować wyniki
pomiaru – wszak informacja, że średnia roczna temperatura w Warszawie
wynosi
jest stałą Boltzmanna. W naturalny sposób w grze pojawia się
więc pojęcie prawdopodobieństwa. Ze względu na statystyczną naturę
opisywanych zagadnień w skończonym układzie parametry termodynamiczne
podlegają zmianom w czasie, przyjmując wartości zbliżone do średniej.
Zmiany te nazywamy fluktuacjami. Oszacowanie wielkości fluktuacji jest
równoznaczne z badaniem odpowiedniego rozkładu prawdopodobieństwa.
Dopiero gdy dysponujemy oszacowaniem wartości średniej i średnim
odchyleniem od tej wartości, jesteśmy w stanie zinterpretować wyniki
pomiaru – wszak informacja, że średnia roczna temperatura w Warszawie
wynosi
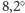 C, nie mówi jeszcze nic o charakterystyce klimatu
i występujących tam różnicach temperatur.
C, nie mówi jeszcze nic o charakterystyce klimatu
i występujących tam różnicach temperatur.
Przyjrzyjmy się dokładniej fluktuacjom „w działaniu” w fizycznym
układzie. Przykładem wielkości fluktuującej wokół swojej średniej
wartości może być liczba cząsteczek gazu (doskonałego) w pewnej
objętości
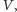 wyodrębnionej z większego układu o objętości
wyodrębnionej z większego układu o objętości
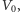 zawierającego
zawierającego
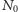 cząsteczek. Wybierając przypadkowy obszar
o objętości
cząsteczek. Wybierając przypadkowy obszar
o objętości
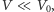 przyjmijmy, że prawdopodobieństwo znalezienia
cząsteczki gazu wewnątrz
przyjmijmy, że prawdopodobieństwo znalezienia
cząsteczki gazu wewnątrz
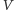 jest dane przez
jest dane przez
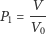 | (2) |
i jest niezależne od kształtu pojemnika z gazem i położeń innych cząsteczek.
Założyliśmy przy tym, że z równym prawdopodobieństwem każda
z cząsteczek gazu przebywa w każdej części układu ze względu na swój ruch
termiczny. Na podstawie tego postulatu Czytelnik może łatwo wykazać, że
rozkład prawdopodobieństwa znalezienia
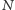 cząsteczek w objętości
cząsteczek w objętości
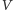 jest rozkładem dwumianowym, ma więc postać
jest rozkładem dwumianowym, ma więc postać
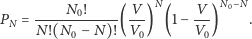 | (3) |
Jeśli teraz rozważymy granicę, gdy układ jest bardzo duży (a zatem
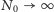 i
i
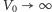 ), ale jednocześnie średnia gęstość gazu
), ale jednocześnie średnia gęstość gazu
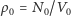 jest stała, możemy znaleźć średnią wartość
jest stała, możemy znaleźć średnią wartość
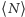 liczby cząstek w objętości
liczby cząstek w objętości
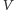
 | (4) |
oraz jej odchylenie standardowe będące miarą odchylenia od wartości średniej
jako
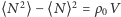 (w granicy). Zbadajmy teraz względne
fluktuacje, czyli stosunek odchylenia od średniej do samej wartości
średniej
(w granicy). Zbadajmy teraz względne
fluktuacje, czyli stosunek odchylenia od średniej do samej wartości
średniej
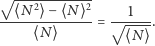 | (5) |
Wnioskujemy stąd, w zgodzie z intuicją, że względne fluktuacje są tym
mniejsze, im większy jest badany podukład (im więcej cząstek zawiera).
Wykorzystując równanie stanu gazu doskonałego
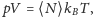 gdzie
gdzie
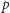 i
i
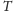 oznaczają ciśnienie i temperaturę gazu w podukładzie,
przepiszmy równanie (5) w postaci
oznaczają ciśnienie i temperaturę gazu w podukładzie,
przepiszmy równanie (5) w postaci
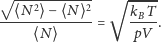 | (6) |
Otrzymana zależność nie jest zbyt użyteczna, bo zawiera parametry
charakteryzujące podukład, o którym niewiele wiemy. Pamiętajmy jednak, że
objętość
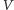 została myślowo wyodrębniona z większego układu
o ustalonej temperaturze
została myślowo wyodrębniona z większego układu
o ustalonej temperaturze
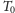 i ciśnieniu
i ciśnieniu
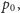 a więc żadne
fizyczne bariery nie oddzielają go od pozostałej objętości, w której spełnione
jest równanie
a więc żadne
fizyczne bariery nie oddzielają go od pozostałej objętości, w której spełnione
jest równanie
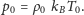
Stąd otrzymujemy
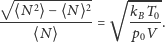 | (7) |
Gdy zwiększamy objętość podukładu, względne fluktuacje zanikają, co jest spodziewane z punktu widzenia termodynamiki.
Przywołajmy kontekst fizyczny otrzymanej zależności – rozważmy obszar
o rozmiarach rzędu długości fali niebieskiego światła, którego długość fali
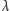 leży w przedziale od 450 do 500 nm. W warunkach normalnych
zawiera on około 3 mln cząsteczek, a względne fluktuacje są na poziomie
leży w przedziale od 450 do 500 nm. W warunkach normalnych
zawiera on około 3 mln cząsteczek, a względne fluktuacje są na poziomie
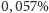 . Odpowiednia wartość fluktuacji dla światła czerwonego
(
. Odpowiednia wartość fluktuacji dla światła czerwonego
(
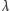 między 610 a 780 nm) to
między 610 a 780 nm) to
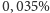 . Fluktuacje tego rzędu
wielkości są z pozoru niewielkie, ale wystarczające, by wywołać niewielkie
różnice współczynnika załamania ośrodka, które z kolei powodują
rozpraszanie światła na tychże fluktuacjach. Jak wskazują obliczone wyżej
wartości, efekt ten jest znacznie silniejszy dla światła niebieskiego, które jest
„bardziej” rozpraszane (konkretnie, natężenie rozproszonego światła jest
proporcjonalne do
. Fluktuacje tego rzędu
wielkości są z pozoru niewielkie, ale wystarczające, by wywołać niewielkie
różnice współczynnika załamania ośrodka, które z kolei powodują
rozpraszanie światła na tychże fluktuacjach. Jak wskazują obliczone wyżej
wartości, efekt ten jest znacznie silniejszy dla światła niebieskiego, które jest
„bardziej” rozpraszane (konkretnie, natężenie rozproszonego światła jest
proporcjonalne do
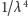 ). Zjawisko to stoi u podstaw wyjaśnienia
niebieskiego koloru nieba, czego dokonali niezależnie Albert Einstein i Marian
Smoluchowski. Przyjrzyjmy się jeszcze jednej makroskopowej wielkości,
mierzonej bezpośrednio w doświadczeniach. Ściśliwość izotermiczna
). Zjawisko to stoi u podstaw wyjaśnienia
niebieskiego koloru nieba, czego dokonali niezależnie Albert Einstein i Marian
Smoluchowski. Przyjrzyjmy się jeszcze jednej makroskopowej wielkości,
mierzonej bezpośrednio w doświadczeniach. Ściśliwość izotermiczna
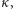 która jest miarą względnej zmiany objętości gazu przy zmianie
ciśnienia i przy stałej temperaturze, dla gazu doskonałego wyraża się
przez
która jest miarą względnej zmiany objętości gazu przy zmianie
ciśnienia i przy stałej temperaturze, dla gazu doskonałego wyraża się
przez
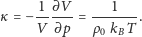 | (8) |
Wynik ten, otrzymany w ramach termodynamiki, możemy teraz porównać z zależnością dla skończonego układu, uzyskaną w ramach mechaniki statystycznej:
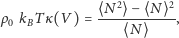 | (9) |
która pozwala zapisać ściśliwość jako
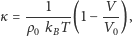 | (10) |
gdzie poprawka jest efektem skończonej objętości podukładu. Efekty
skończoności układu (ang. finite-size effects) odgrywają istotną rolę
w symulacjach komputerowych. Komputery są potężnym narzędziem,
pozwalającym na badanie dynamiki dużych układów; można dziś np.
numerycznie rozwiązać równania ruchu
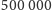 atomów w ciągu 500
ns. Trzeba jednak zawsze pamiętać, że symulujemy skończony podukład,
a nie układ w granicy termodynamicznej, a badane przez nas wielkości (np.
ściśliwość) zależą od wielkości układu. Mówiąc obrazowo, do
„nieskończoności” trzeba podejść najbliżej, jak tylko się da, a dalej
można tylko zastanowić się, na ile skończoność układu wpływa na wynik
pomiaru.
atomów w ciągu 500
ns. Trzeba jednak zawsze pamiętać, że symulujemy skończony podukład,
a nie układ w granicy termodynamicznej, a badane przez nas wielkości (np.
ściśliwość) zależą od wielkości układu. Mówiąc obrazowo, do
„nieskończoności” trzeba podejść najbliżej, jak tylko się da, a dalej
można tylko zastanowić się, na ile skończoność układu wpływa na wynik
pomiaru.
Operacja powiększania układu (objętości, liczby cząsteczek) przy jednoczesnym
utrzymaniu lokalnych wielkości (np. średniej gęstości) prowadzi do granicy
termodynamicznej – przy przejściu do tej granicy w układzie zanikają
fluktuacje, a zatem wielkości, które charakteryzują jego stan (takie
jak temperatura czy ciśnienie), nie zmieniają się w czasie. Wówczas
termodynamika fenomenologiczna staje się ścisłą teorią. Dla typowych
układów makroskopowych (gdzie
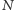 jest rzędu liczby Avogadra
jest rzędu liczby Avogadra
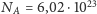 ) fluktuacje są pomijalne, dlatego opis fenomenologiczny
pozwala tak dokładnie przewidzieć własności termodynamiczne wielu
substancji.
) fluktuacje są pomijalne, dlatego opis fenomenologiczny
pozwala tak dokładnie przewidzieć własności termodynamiczne wielu
substancji.
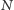 spośród
spośród
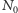 cząsteczek. Jak wygląda wykres tej gęstości prawdopodobieństwa
w zależności od
cząsteczek. Jak wygląda wykres tej gęstości prawdopodobieństwa
w zależności od
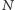 dla różnych wartości parametrów
dla różnych wartości parametrów
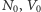 i
i