Zadanie ZM-1560
o zadaniu...
- Publikacja w Delcie: marzec 2018
- Publikacja elektroniczna: 28 lutego 2018
Wyznaczyć iloczyn długości wszystkich boków i przekątnych 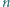 -kąta foremnego wpisanego w okrąg o promieniu 1.
-kąta foremnego wpisanego w okrąg o promieniu 1.
Wyznaczyć iloczyn długości wszystkich boków i przekątnych 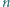 -kąta foremnego wpisanego w okrąg o promieniu 1.
-kąta foremnego wpisanego w okrąg o promieniu 1.
Zadanie 758 zaproponował pan Witold Bednarek z Łodzi.
Trzy okręgi o promieniach 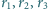 są parami styczne zewnętrznie oraz są styczne wewnętrznie do okręgu o promieniu
są parami styczne zewnętrznie oraz są styczne wewnętrznie do okręgu o promieniu 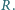 Wykazać, że
Wykazać, że

Wewnątrz sześciokąta wypukłego 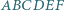 leży taki punkt
leży taki punkt 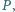 że spełnione są równości
że spełnione są równości 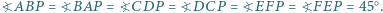 Udowodnij, że suma długości odcinków
Udowodnij, że suma długości odcinków 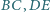 i
i 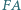 jest nie mniejsza od każdego z odcinków
jest nie mniejsza od każdego z odcinków 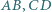 i
i 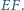
Dany jest pięciokąt wypukły 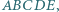 w którym
w którym 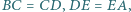
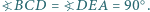 Udowodnij, że z odcinków o długościach
Udowodnij, że z odcinków o długościach 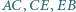 można zbudować trójkąt. Wyznacz miary jego kątów, znając miarę
można zbudować trójkąt. Wyznacz miary jego kątów, znając miarę  kąta
kąta 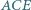 i miarę
i miarę 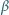 kąta
kąta 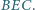
W sześciokącie wypukłym 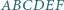 wszystkie boki są równej długości oraz
wszystkie boki są równej długości oraz 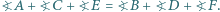 Udowodnij, że przekątne
Udowodnij, że przekątne 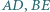 i
i 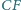 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
Mamy do dyspozycji cztery wycięte z papieru przystające trójkąty prostokątne. Możemy wielokrotnie wykonywać operację polegającą na wybraniu jednego z kawałków i rozcięciu go wzdłuż wysokości, poprowadzonej z wierzchołka kąta prostego, na dwa mniejsze trójkąty prostokątne. Wykazać, że po wykonaniu skończonej liczby cięć zawsze co najmniej dwa kawałki będą przystające.
W czworokącie wypukłym 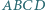 punkty
punkty 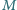 i
i 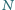 są odpowiednio środkami boków
są odpowiednio środkami boków 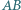 i
i 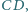 zaś przekątne przecinają się w punkcie
zaś przekątne przecinają się w punkcie 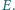 Wykazać, że prosta zawierająca dwusieczną kąta
Wykazać, że prosta zawierająca dwusieczną kąta 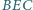 jest prostopadła do prostej
jest prostopadła do prostej 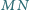 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 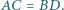
Dany jest czworokąt 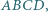 w którym
w którym 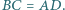 Na bokach
Na bokach 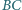 i
i 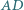 zbudowano na zewnątrz takie trójkąty
zbudowano na zewnątrz takie trójkąty 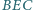 i
i 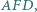 że
że 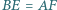 oraz
oraz 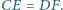 Udowodnić, że środki odcinków
Udowodnić, że środki odcinków 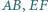 i
i 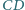 leżą na jednej prostej.
leżą na jednej prostej.
Na płaszczyźnie dane są kwadraty 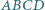 oraz
oraz 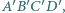 przeciwnie zorientowane o bokach odpowiednio długości
przeciwnie zorientowane o bokach odpowiednio długości 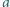 i
i 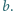 Punkty
Punkty 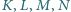 leżą odpowiednio na odcinkach
leżą odpowiednio na odcinkach 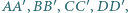 przy czym
przy czym

Dowieść, że punkty 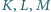 i
i 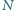 leżą na jednej prostej.
leżą na jednej prostej.
Częścią wspólną dwóch jednakowych kwadratów jest ośmiokąt. Boki jednego z kwadratów zostały narysowane na czerwono, drugiego zaś na niebiesko. Udowodnić, że suma długości czerwonych boków ośmiokąta jest równa sumie długości jego niebieskich boków.
Wewnątrz trójkąta 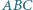 leży punkt
leży punkt 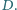 Proste
Proste 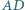 i
i 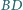 przecinają boki
przecinają boki 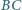 i
i 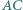 odpowiednio w punktach
odpowiednio w punktach 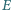 i
i 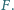 Udowodnić, że jeśli
Udowodnić, że jeśli 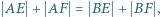 to
to 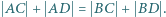
Dany jest okrąg 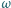 o średnicy
o średnicy 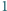 oraz łamana
oraz łamana  o końcach należących do tego okręgu, której długość jest mniejsza od
o końcach należących do tego okręgu, której długość jest mniejsza od  Udowodnić, że istnieje średnica okręgu
Udowodnić, że istnieje średnica okręgu 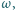 która jest rozłączna z
która jest rozłączna z 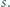
Trójkąt równoboczny o boku długości 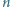 został podzielony (prostymi równoległymi do boków) na
został podzielony (prostymi równoległymi do boków) na 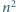 trójkątów o boku 1 (trójkątów jednostkowych). Wierzchołkom powstałej siatki zostały przyporządkowane różne liczby rzeczywiste (
trójkątów o boku 1 (trójkątów jednostkowych). Wierzchołkom powstałej siatki zostały przyporządkowane różne liczby rzeczywiste ( 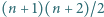 różnych liczb). Trójkąt jednostkowy nazwiemy zorientowanym dodatnio, jeśli - idąc wzdłuż jego brzegu, w kierunku wzrastania liczb przy wierzchołkach (tj. startując od najmniejszej i idąc przez średnią do największej) - mamy jego wnętrze po lewej stronie. Dla ustalonej liczby naturalnej
różnych liczb). Trójkąt jednostkowy nazwiemy zorientowanym dodatnio, jeśli - idąc wzdłuż jego brzegu, w kierunku wzrastania liczb przy wierzchołkach (tj. startując od najmniejszej i idąc przez średnią do największej) - mamy jego wnętrze po lewej stronie. Dla ustalonej liczby naturalnej  wyznaczyć najmniejszą i największą możliwą wartość liczby trójkątów jednostkowych zorientowanych dodatnio.
wyznaczyć najmniejszą i największą możliwą wartość liczby trójkątów jednostkowych zorientowanych dodatnio.