Zadanie ZM-1512
o zadaniu...
- Publikacja w Delcie: listopad 2016
- Publikacja elektroniczna: 1 listopada 2016
Dany jest sześciokąt wypukły 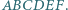 Każda z przekątnych
Każda z przekątnych 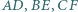 dzieli ten sześciokąt na dwa czworokąty o równych polach. Udowodnij, że przekątne te przecinają się w jednym punkcie.
dzieli ten sześciokąt na dwa czworokąty o równych polach. Udowodnij, że przekątne te przecinają się w jednym punkcie.
Twierdzenie (Pascala). Punkty 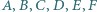 leżą na jednym okręgu. Proste
leżą na jednym okręgu. Proste 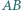 i
i 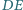 przecinają się w punkcie
przecinają się w punkcie 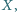 proste
proste 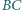 i
i 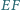 w punkcie
w punkcie 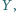 proste
proste 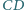 i
i 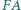 w punkcie
w punkcie 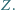 Wykaż, że wówczas punkty
Wykaż, że wówczas punkty 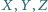 leżą na jednej prostej.
leżą na jednej prostej.
Okręgi 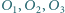 są styczne odpowiednio do par boków
są styczne odpowiednio do par boków 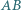 i
i 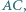
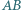 i
i 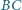 oraz
oraz 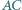 i
i 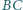 trójkąta
trójkąta 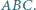 Okrąg
Okrąg 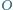 jest styczny zewnętrznie do okręgów
jest styczny zewnętrznie do okręgów 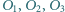 odpowiednio w punktach
odpowiednio w punktach 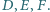 Wykaż, że proste
Wykaż, że proste 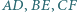 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
Dany jest równoległobok 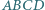 oraz punkt
oraz punkt 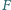 leżący na odcinku
leżący na odcinku 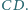 Punkty
Punkty 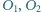 i
i 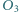 są środkami okręgów opisanych na trójkątach
są środkami okręgów opisanych na trójkątach 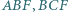 i
i 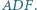 Dowieść, że ortocentrum trójkąta
Dowieść, że ortocentrum trójkąta 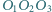 leży na prostej
leży na prostej 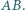
W czworokącie 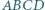 opisanym na okręgu prosta
opisanym na okręgu prosta 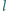 przechodząca przez wierzchołek
przechodząca przez wierzchołek 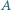 przecina bok
przecina bok 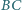 w punkcie
w punkcie 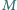 oraz półprostą
oraz półprostą 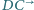 w punkcie
w punkcie 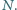 Punkty
Punkty 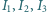 są środkami okręgów wpisanych odpowiednio w trójkąty
są środkami okręgów wpisanych odpowiednio w trójkąty 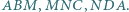 Dowieść, że punkt przecięcia wysokości trójkąta
Dowieść, że punkt przecięcia wysokości trójkąta 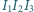 leży na prostej
leży na prostej 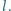
Dane są punkty 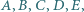 takie, że czworokąt
takie, że czworokąt 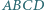 jest równoległobokiem, a czworokąt
jest równoległobokiem, a czworokąt 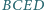 jest wpisany w okrąg. Prosta
jest wpisany w okrąg. Prosta 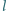 przechodząca przez
przechodząca przez 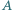 przecina wnętrze odcinka
przecina wnętrze odcinka 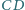 w punkcie
w punkcie 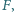 a prostą
a prostą 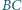 w punkcie
w punkcie 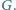 Przypuśćmy, że
Przypuśćmy, że 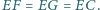 Wykazać, że
Wykazać, że 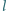 jest dwusieczną kąta
jest dwusieczną kąta 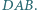
Dany jest trójkąt 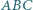 wpisany w okrąg
wpisany w okrąg 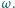 Punkt
Punkt 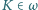 i punkt
i punkt 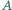 leżą po przeciwnych stronach prostej
leżą po przeciwnych stronach prostej 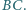 Punkty
Punkty 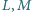 są odbiciami punktu
są odbiciami punktu 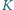 względem
względem 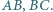 Okrąg przechodzący przez punkty
Okrąg przechodzący przez punkty 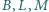 przecina
przecina 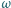 po raz drugi w punkcie
po raz drugi w punkcie 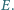 Punkt
Punkt 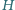 jest ortocentrum trójkąta
jest ortocentrum trójkąta 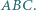 Wykazać, że proste
Wykazać, że proste 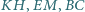 mają punkt wspólny.
mają punkt wspólny.
W trójkącie 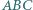 okrąg wpisany jest styczny do boków
okrąg wpisany jest styczny do boków 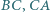 i
i 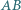 w punktach odpowiednio
w punktach odpowiednio 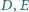 i
i 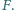 Punkt
Punkt 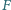 jest punktem Feuerbacha trójkąta
jest punktem Feuerbacha trójkąta 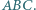 Wówczas prosta Simsona punktu
Wówczas prosta Simsona punktu 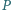 względem trójkąta
względem trójkąta 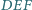 jest równoległa do prostej
jest równoległa do prostej 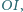 która łączy środki
która łączy środki 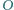 i
i 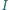 - okręgów opisanego i wpisanego trójkąta
- okręgów opisanego i wpisanego trójkąta 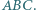
Czworokąt wypukły 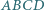 o obwodzie
o obwodzie 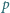 został podzielony przekątnymi na cztery trójkąty. Środki okręgów wpisanych w te trójkąty tworzą czworokąt o obwodzie
został podzielony przekątnymi na cztery trójkąty. Środki okręgów wpisanych w te trójkąty tworzą czworokąt o obwodzie 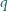 . Wykazać, że pole
. Wykazać, że pole 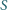 czworokąta
czworokąta 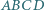 jest mniejsze niż
jest mniejsze niż 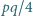 .
.
Z kostek domina o wymiarach 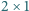 ułożono szachownicę
ułożono szachownicę 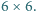 Wykaż, że istnieje taka prosta równoległa do jednego z boków szachownicy i przechodząca przez jej wnętrze, która nie rozcina żadnej z kostek domina.
Wykaż, że istnieje taka prosta równoległa do jednego z boków szachownicy i przechodząca przez jej wnętrze, która nie rozcina żadnej z kostek domina.
Udowodnij, że po usunięciu z kwadratu o krawędzi 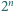 dowolnego spośród
dowolnego spośród 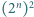 tworzących go kwadratów jednostkowych powstaje figura, którą daje się szczelnie wypełnić klockami
tworzących go kwadratów jednostkowych powstaje figura, którą daje się szczelnie wypełnić klockami 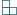 , zbudowanymi z trzech kwadratów jednostkowych.
, zbudowanymi z trzech kwadratów jednostkowych.
W czworokącie wypukłym 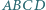 kąty przy wierzchołkach
kąty przy wierzchołkach 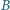 i
i 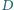 są proste. Przekątne przecinają się w punkcie
są proste. Przekątne przecinają się w punkcie 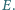 Prosta prostopadła do
Prosta prostopadła do 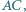 przechodząca przez punkt
przechodząca przez punkt 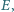 przecina proste
przecina proste 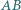 i
i 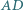 w punktach
w punktach 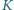 i
i 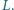 Wykazać, że punkty
Wykazać, że punkty 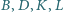 leżą na jednym okręgu.
leżą na jednym okręgu.
Punkty 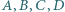 leżą kolejno na okręgu
leżą kolejno na okręgu 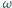 w taki sposób, że cięciwy
w taki sposób, że cięciwy 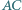 i
i 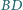 przecinają się pod kątem prostym. Obliczyć promień
przecinają się pod kątem prostym. Obliczyć promień  okręgu
okręgu 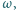 jeśli cięciwy
jeśli cięciwy 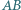 i
i 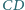 mają odpowiednio długości
mają odpowiednio długości 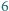 i
i 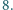
Boki 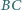 i
i 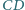 prostokąta
prostokąta 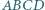 są styczne odpowiednio w punktach
są styczne odpowiednio w punktach 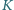 i
i 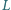 do okręgu przechodzącego przez
do okręgu przechodzącego przez 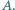 Na odcinku
Na odcinku 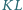 leży taki punkt
leży taki punkt 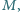 że proste
że proste 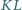 i
i 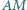 są prostopadłe. Obliczyć pole prostokąta
są prostopadłe. Obliczyć pole prostokąta 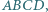 wiedząc, że odcinek
wiedząc, że odcinek 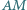 ma długość
ma długość 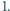
Trójkąt 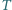 rozcięto wzdłuż odcinka na dwa trójkąty
rozcięto wzdłuż odcinka na dwa trójkąty 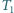 i
i 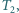 a trójkąt
a trójkąt 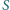 - na trójkąty
- na trójkąty 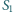 i
i 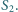 Okazało się, że trójkąt
Okazało się, że trójkąt 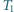 jest przystający do trójkąta
jest przystający do trójkąta 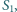 a trójkąt
a trójkąt 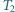 jest przystający do trójkąta
jest przystający do trójkąta 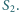 Czy wynika z tego, że trójkąty
Czy wynika z tego, że trójkąty 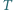 i
i 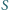 są przystające?
są przystające?
Dane są trójkąty 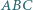 i
i 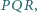 przy czym
przy czym 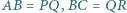 oraz
oraz 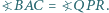 Czy wynika z tego, że trójkąty te są przystające?
Czy wynika z tego, że trójkąty te są przystające?
Trójkąty 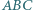 i
i 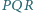 mają równe pola oraz
mają równe pola oraz 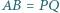 i
i 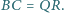 Czy wynika z tego, że trójkąty te są przystające?
Czy wynika z tego, że trójkąty te są przystające?
Czworokąty wypukłe 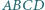 i
i 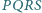 mają równe pola oraz
mają równe pola oraz 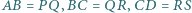 i
i 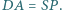 Czy wynika z tego, że czworokąty te są przystające?
Czy wynika z tego, że czworokąty te są przystające?
Przekątna pewnego czworokąta wypukłego dzieli go na dwa trójkąty równoramienne. Czy wynika z tego, że czworokąt ten jest deltoidem lub równoległobokiem?