Zadanie ZM-1547
o zadaniu...
- Publikacja w Delcie: listopad 2017
- Publikacja elektroniczna: 31 października 2017
Trójkąt 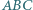 jest opisany na okręgu o środku
jest opisany na okręgu o środku 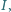 stycznym do boków
stycznym do boków 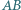 i
i 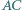 w punktach
w punktach 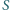 i
i 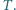 Na boku
Na boku 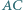 leży taki punkt
leży taki punkt 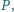 że
że 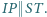 Proste
Proste 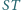 i
i 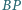 przecinają się w punkcie
przecinają się w punkcie 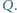 Dowieść, że
Dowieść, że 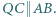
Punkt 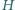 jest ortocentrum trójkąta ostrokątnego
jest ortocentrum trójkąta ostrokątnego 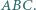 Wykaż, że okręgi opisane na trójkątach
Wykaż, że okręgi opisane na trójkątach 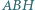 i
i 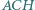 są przystające.
są przystające.
Na obwodzie trójkąta 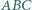 leżą cztery różne punkty
leżą cztery różne punkty 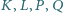 : punkty
: punkty 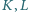 na boku
na boku 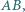 punkty
punkty 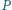 i
i 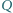 odpowiednio na bokach
odpowiednio na bokach 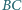 i
i 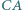 ; przy tym odcinki
; przy tym odcinki 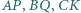 i
i 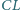 mają jednakową długość. Udowodnić, że środki tych czterech odcinków leżą na jednym okręgu.
mają jednakową długość. Udowodnić, że środki tych czterech odcinków leżą na jednym okręgu.
Rozstrzygnij, czy istnieje takich 100 punktów na płaszczyźnie, z których każde trzy są wierzchołkami trójkąta rozwartokątnego.
Podziel kwadrat na 8 trójkątów ostrokątnych.
Zadanie 4 jest modyfikacją zadania z XXV Olimpiady Matematycznej. Więcej o nim m.in. w Delcie 5/1986.
W czworościanie 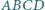 krawędź
krawędź 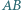 jest prostopadła do krawędzi
jest prostopadła do krawędzi 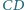 i
i 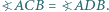 Rozstrzygnij, czy oznacza to, że płaszczyzna wyznaczona przez krawędź
Rozstrzygnij, czy oznacza to, że płaszczyzna wyznaczona przez krawędź 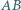 i środek krawędzi
i środek krawędzi 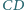 jest prostopadła do krawędzi
jest prostopadła do krawędzi 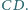
Skonstruuj trójkąt 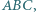 mając dane punkty
mając dane punkty 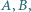 kąt przy wierzchołku
kąt przy wierzchołku 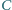 oraz długość środkowej
oraz długość środkowej 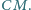 Ile rozwiązań może mieć to zadanie?
Ile rozwiązań może mieć to zadanie?
Punkty 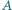 i
i 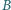 należą do wnętrza kąta ostrego
należą do wnętrza kąta ostrego 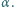 Skonstruuj taki trójkąt równoramienny, aby punkty
Skonstruuj taki trójkąt równoramienny, aby punkty 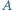 i
i 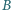 należały do różnych jego ramion, aby podstawa tego trójkąta była zawarta w jednym z ramion kąta
należały do różnych jego ramion, aby podstawa tego trójkąta była zawarta w jednym z ramion kąta 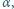 a wierzchołek należał do drugiego z ramion.
a wierzchołek należał do drugiego z ramion.
Udowodnij stwierdzenia z drugiego akapitu niniejszego artykułu.
Niech 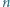 będzie liczbą naturalną większą od 4. Udowodnić, że w elipsę o półosiach różnej długości nie można wpisać
będzie liczbą naturalną większą od 4. Udowodnić, że w elipsę o półosiach różnej długości nie można wpisać 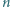 -kąta foremnego.
-kąta foremnego.
W dwa trójkąty, o bokach odpowiednio 17, 25, 26 i 17, 25, 28, wpisujemy koła. Które z wpisanych kół ma większy promień?
Dwa okręgi, styczne zewnętrznie w punkcie 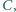 są styczne do prostej
są styczne do prostej 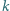 w punktach
w punktach 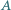 i
i 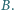 Wykaż, że trójkąt
Wykaż, że trójkąt 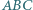 jest prostokątny.
jest prostokątny.
Wykaż, że jeżeli przekątne pewnego trapezu są prostopadłe, to suma długości podstaw tego trapezu jest nie większa od sumy długości jego ramion.
Wewnątrz kwadratu 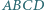 wybrano taki punkt
wybrano taki punkt 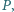 że
że 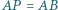 oraz
oraz 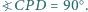 Wykaż, że
Wykaż, że 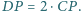
W trójkącie 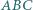 środkowe poprowadzone z wierzchołków
środkowe poprowadzone z wierzchołków 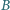 i
i 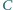 są prostopadłe oraz
są prostopadłe oraz 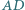 jest wysokością. Wykaż, że
jest wysokością. Wykaż, że 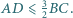
Okrąg wpisany w trójkąt 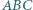 jest styczny do boków
jest styczny do boków 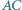 i
i 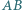 odpowiednio w punktach
odpowiednio w punktach 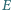 i
i 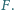 Punkt
Punkt 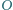 jest środkiem tego okręgu, a punkt
jest środkiem tego okręgu, a punkt 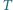 jest symetryczny do punktu
jest symetryczny do punktu 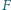 względem punktu
względem punktu 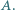 Wykaż, że proste
Wykaż, że proste 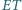 i
i 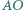 są równoległe.
są równoległe.
Proste 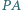 i
i 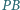 są styczne do okręgu
są styczne do okręgu 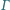 odpowiednio w punktach
odpowiednio w punktach 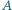 i
i 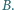 Punkt
Punkt 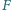 jest rzutem prostokątnym punktu
jest rzutem prostokątnym punktu 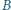 na średnicę
na średnicę 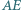 okręgu
okręgu 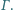 Wykaż, że środek odcinka
Wykaż, że środek odcinka 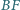 leży na prostej
leży na prostej