W krzywym zwierciadle»Zadanie 5
o zadaniu...
- Zadanie pochodzi z artykułu W krzywym zwierciadle
- Publikacja w Delcie: maj 2013
- Publikacja elektroniczna: 30-04-2013
- Artykuł źródłowy w wersji do druku [application/pdf]: (68 KB)
W czworokącie wypukłym
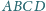 okręgi wpisane w trójkąty
okręgi wpisane w trójkąty
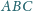 i
i
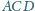 są styczne. Wykaż, że ich punkty styczności
z bokami czworokąta leżą na jednym okręgu.
są styczne. Wykaż, że ich punkty styczności
z bokami czworokąta leżą na jednym okręgu.
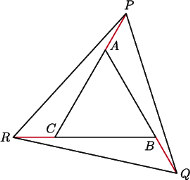
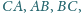 będących przedłużeniami boków
trójkąta
będących przedłużeniami boków
trójkąta
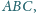 obrano odpowiednio punkty
obrano odpowiednio punkty
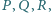 przy czym
przy czym
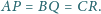 Udowodnić, że jeśli trójkąt
Udowodnić, że jeśli trójkąt
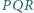 jest
równoboczny, to trójkąt
jest
równoboczny, to trójkąt
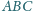 również.
również.
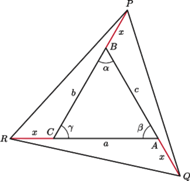
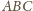 jak na rysunku
i załóżmy, że
jak na rysunku
i załóżmy, że
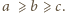
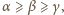 a stąd
a stąd
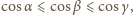 ponieważ
funkcja
ponieważ
funkcja
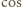 jest malejąca na przedziale
jest malejąca na przedziale
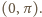 Przyjmijmy,
że
Przyjmijmy,
że
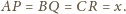 Wówczas z twierdzenia cosinusów
otrzymujemy
Wówczas z twierdzenia cosinusów
otrzymujemy
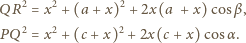
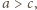 to ponieważ
to ponieważ
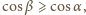 mielibyśmy
mielibyśmy
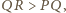 co przeczyłoby założeniu, że trójkąt
co przeczyłoby założeniu, że trójkąt
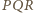 jest
równoboczny. W takim razie
jest
równoboczny. W takim razie
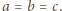
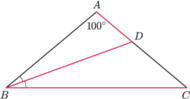
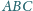 kąt przy wierzchołku
kąt przy wierzchołku
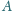 ma
miarę
ma
miarę
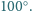 Dwusieczna kąta przy wierzchołku
Dwusieczna kąta przy wierzchołku
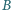 przecina bok
przecina bok
 w punkcie
w punkcie
 Udowodnić, że
Udowodnić, że
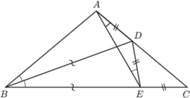
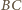 taki punkt
taki punkt
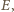 że
że
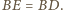
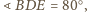 a skoro
a skoro
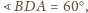 to
to
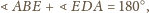
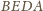 można opisać okrąg. Wobec tego
można opisać okrąg. Wobec tego
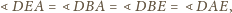
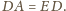 Z drugiej strony,
Z drugiej strony,
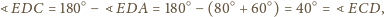
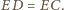 Zatem
Zatem
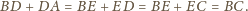
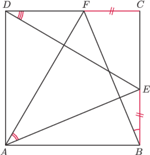
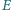 i
i
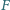 leżą odpowiednio na bokach
leżą odpowiednio na bokach
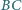 i
i
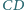 kwadratu
kwadratu
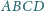 o boku 1, przy czym
o boku 1, przy czym
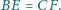 Udowodnij, że
Udowodnij, że
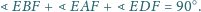
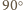 wokół środka. Obrazem trójkąta
wokół środka. Obrazem trójkąta
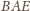 jest trójkąt
jest trójkąt
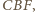 zatem
zatem
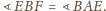 Analogicznie
Analogicznie
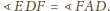 Stąd
Stąd
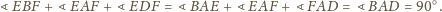
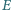 i
i
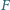 leżą odpowiednio na bokach
leżą odpowiednio na bokach
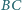 i
i
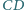 kwadratu
kwadratu
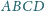 o boku 1, przy czym
o boku 1, przy czym
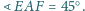 Wykaż, że
Wykaż, że
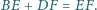
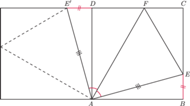
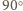 wokół wierzchołka
wokół wierzchołka
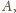 niech
niech
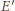 będzie obrazem punktu
będzie obrazem punktu
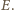 Wtedy
Wtedy
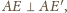 zatem
zatem
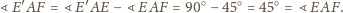
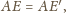 więc
więc
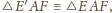 bo trójkąty te mają
dodatkowo wspólny bok
bo trójkąty te mają
dodatkowo wspólny bok
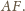 Stąd
Stąd
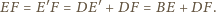
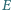 i
i
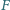 leżą odpowiednio na bokach
leżą odpowiednio na bokach
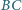 i
i
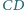 kwadratu
kwadratu
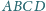 o boku 1, przy czym obwód
trójkąta
o boku 1, przy czym obwód
trójkąta
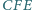 równy jest 2. Wyznacz miarę kąta
równy jest 2. Wyznacz miarę kąta
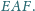
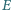 i
i
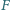 leżą odpowiednio na bokach
leżą odpowiednio na bokach
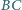 i
i
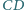 kwadratu
kwadratu
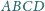 o boku 1, przy czym
o boku 1, przy czym
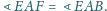 Wykaż, że
Wykaż, że
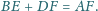
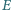 i
i
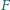 leżą odpowiednio na bokach
leżą odpowiednio na bokach
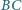 i
i
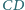 kwadratu
kwadratu
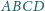 o boku 1, przy czym
o boku 1, przy czym
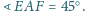 Oblicz wysokość trójkąta
Oblicz wysokość trójkąta
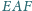 poprowadzoną
z wierzchołka
poprowadzoną
z wierzchołka
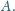
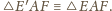 Wysokości tych
trójkątów poprowadzone z wierzchołka
Wysokości tych
trójkątów poprowadzone z wierzchołka
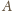 są więc obie równe
są więc obie równe
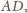 czyli 1.
czyli 1.
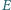 i
i
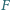 leżą odpowiednio na bokach
leżą odpowiednio na bokach
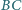 i
i
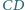 kwadratu
kwadratu
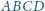 o boku 1, przy czym
o boku 1, przy czym
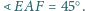 Proste
Proste
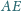 i
i
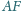 przecinają przekątną
przecinają przekątną
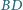 odpowiednio w punktach
odpowiednio w punktach
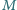 i
i
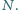 Proste
Proste
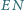 i
i
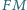 przecinają się w punkcie
przecinają się w punkcie
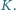 Wykaż, że proste
Wykaż, że proste
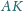 i
i
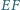 są prostopadłe.
są prostopadłe.
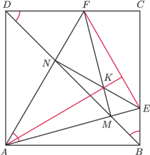
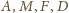 leżą na jednym okręgu, bo
leżą na jednym okręgu, bo
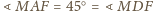 i punkty
i punkty
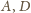 leżą po tej samej stronie prostej
leżą po tej samej stronie prostej
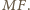 Kąt
Kąt
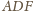 jest
prosty, więc
jest
prosty, więc
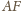 jest średnicą tego okręgu. Stąd
jest średnicą tego okręgu. Stąd
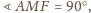 zatem
zatem
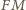 jest wysokością trójkąta
jest wysokością trójkąta
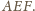 Analogicznie
Analogicznie
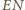 jest
wysokością tego trójkąta, więc
jest
wysokością tego trójkąta, więc
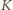 to jego ortocentrum. Wobec tego
to jego ortocentrum. Wobec tego
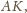 jako trzecia wysokość, jest prostopadła do
jako trzecia wysokość, jest prostopadła do
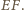
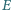 i
i
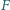 leżą odpowiednio na bokach
leżą odpowiednio na bokach
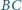 i
i
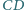 kwadratu
kwadratu
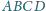 o boku 1, przy czym prosta
o boku 1, przy czym prosta
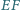 jest styczna do okręgu o środku
jest styczna do okręgu o środku
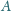 i promieniu 1. Proste
i promieniu 1. Proste
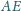 i
i
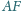 przecinają przekątną
przecinają przekątną
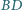 odpowiednio w punktach
odpowiednio w punktach
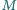 i
i
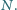 Udowodnij, że punkty
Udowodnij, że punkty
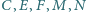 leżą na
jednym okręgu.
leżą na
jednym okręgu.
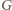 będzie punktem styczności prostej
będzie punktem styczności prostej
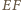 do danego
okręgu. Wtedy
do danego
okręgu. Wtedy
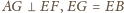 oraz
oraz
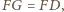 zatem
zatem
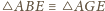 oraz
oraz
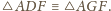 Stąd
Stąd
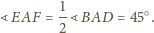
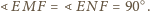
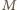 i
i
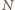 leżą na okręgu o średnicy
leżą na okręgu o średnicy
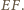 Leży na nim też punkt
Leży na nim też punkt
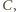 bo
bo
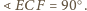
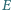 i
i
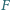 leżą odpowiednio na bokach
leżą odpowiednio na bokach
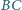 i
i
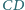 kwadratu
kwadratu
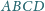 o boku 1, przy czym
o boku 1, przy czym
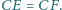 Punkt
Punkt
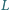 to rzut punktu
to rzut punktu
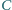 na prostą
na prostą
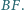 Wykaż, że
Wykaż, że
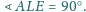
 wokół środka. Obrazem punktu
wokół środka. Obrazem punktu
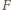 jest
taki punkt
jest
taki punkt
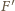 na boku
na boku
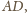 że
że
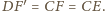 Obrazem
prostej
Obrazem
prostej
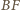 jest prosta
jest prosta
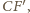 jest ona prostopadła do
jest ona prostopadła do
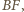 więc
zawiera punkt
więc
zawiera punkt
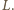 Opiszmy okrąg na prostokącie
Opiszmy okrąg na prostokącie
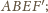 jego
średnicą jest
jego
średnicą jest
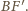 Punkt
Punkt
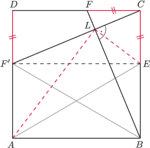
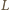 leży na tym okręgu, ponieważ kąt
leży na tym okręgu, ponieważ kąt
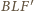 jest prosty. Średnicą okręgu jest także
jest prosty. Średnicą okręgu jest także
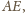 więc również
kąt
więc również
kąt
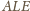 jest prosty.
jest prosty.
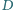 leży na boku
leży na boku
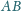 trójkąta
trójkąta
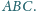 Punkt
Punkt
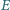 jest środkiem okręgu dopisanego, stycznego do boku
jest środkiem okręgu dopisanego, stycznego do boku
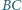 oraz
przedłużeń boków
oraz
przedłużeń boków
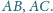 Punkt
Punkt
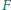 jest środkiem
okręgu wpisanego w trójkąt
jest środkiem
okręgu wpisanego w trójkąt
 Dowieść, że jeżeli trójkąt
Dowieść, że jeżeli trójkąt
 jest równoramienny, to także trójkąt
jest równoramienny, to także trójkąt
 jest
równoramienny.
jest
równoramienny.
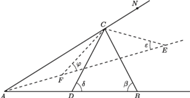
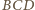 przy wierzchołkach
przy wierzchołkach
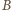 i
i
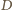 przez
przez
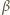 i
i
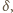 a miary kątów trójkąta
a miary kątów trójkąta
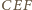 przy
wierzchołkach
przy
wierzchołkach
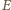 i
i
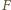 przez
przez
 i
i
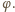
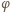 i
i
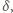 jako kąty zewnętrzne trójkątów
jako kąty zewnętrzne trójkątów
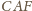 i
i
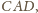 są związane zależnością
są związane zależnością
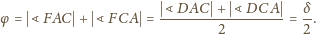
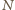 będzie dowolnym punktem na przedłużeniu boku
będzie dowolnym punktem na przedłużeniu boku
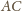 poza wierzchołek
poza wierzchołek
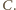 Kąty
Kąty
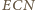 i
i
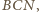 jako
kąty zewnętrzne trójkątów
jako
kąty zewnętrzne trójkątów
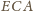 i
i
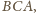 wyrażają się
jako sumy:
wyrażają się
jako sumy:
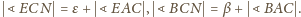 Tak
więc
Tak
więc
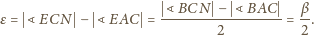
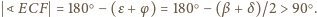 Zatem jeśli
trójkąt
Zatem jeśli
trójkąt
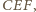 z kątem rozwartym przy wierzchołku
z kątem rozwartym przy wierzchołku
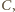 jest
równoramienny, to
jest
równoramienny, to
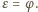 Z uzyskanych wcześniej równości
dostajemy wówczas
Z uzyskanych wcześniej równości
dostajemy wówczas
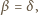 czyli równoramienność trójkąta
czyli równoramienność trójkąta
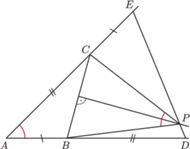
 i takie punkty
i takie punkty
 i
i
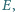 że
że
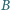 leży na odcinku
leży na odcinku
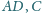 leży na odcinku
leży na odcinku
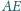 oraz
zachodzą równości
oraz
zachodzą równości
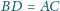 i
i
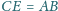 (rysunek). Symetralna
odcinka
(rysunek). Symetralna
odcinka
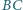 przecina
przecina
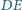 w punkcie
w punkcie
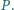 Udowodnić, że
kąty
Udowodnić, że
kąty
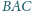 i
i
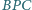 są równe.
są równe.
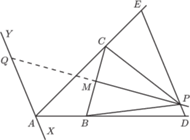
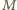 jest środkiem
jest środkiem
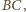 jego odległość od prostej
jego odległość od prostej
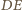 to średnia arytmetyczna odległości punktów
to średnia arytmetyczna odległości punktów
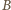 i
i
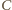 od
od
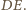 Jest ona równa średniej arytmetycznej odległości tych punktów
od
Jest ona równa średniej arytmetycznej odległości tych punktów
od
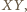 ponieważ
ponieważ
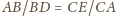 i
i
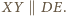 Zatem
Zatem
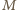 jest równo odległy od
jest równo odległy od
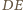 i
i
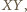 skąd
skąd
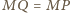 oraz
oraz
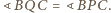
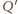 będzie takim punktem na półprostej
będzie takim punktem na półprostej
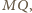 że
że
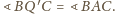 Z podobieństwa trójkątów równoramiennych
Z podobieństwa trójkątów równoramiennych
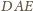 i
i
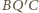 mamy
mamy
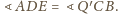 Zatem skoro na
czworokącie
Zatem skoro na
czworokącie
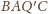 można opisać okrąg, to
można opisać okrąg, to
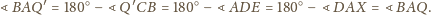
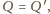 co daje tezę.
co daje tezę.
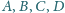 leżą, w tej właśnie kolejności, na prostej
leżą, w tej właśnie kolejności, na prostej
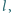 przy
czym
przy
czym
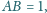
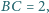
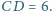 Rozstrzygnij, czy istnieje taki
punkt
Rozstrzygnij, czy istnieje taki
punkt
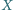 spoza prostej
spoza prostej
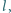 aby
aby
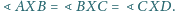

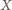 istnieje, to
istnieje, to
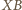 jest dwusieczną kąta
jest dwusieczną kąta
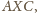 zatem z twierdzenia o dwusiecznej
zatem z twierdzenia o dwusiecznej
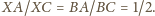 Punkty
Punkty
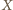 i
i
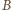 leżą więc na okręgu Apoloniusza dla punktów
leżą więc na okręgu Apoloniusza dla punktów
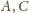 i stałej 1/2. Analogicznie punkty
i stałej 1/2. Analogicznie punkty
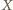 i
i
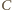 leżą na
okręgu Apoloniusza dla punktów
leżą na
okręgu Apoloniusza dla punktów
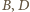 i stałej 1/3.
i stałej 1/3.

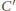 na prostej
na prostej
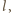 różny od
różny od
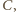 spełnia
warunek
spełnia
warunek
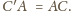 Wtedy
Wtedy
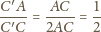
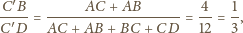
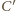 należy do obydwu powyższych okręgów. Średnicą
pierwszego z nich jest więc
należy do obydwu powyższych okręgów. Średnicą
pierwszego z nich jest więc
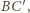 a drugiego –
a drugiego –
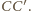 Stąd jedynym
ich wspólnym punktem jest
Stąd jedynym
ich wspólnym punktem jest
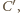 czyli
czyli
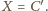 Ale wtedy
Ale wtedy
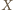 leży na prostej
leży na prostej
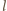 – sprzeczność.
– sprzeczność.
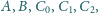 przy czym
przy czym
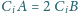 dla
dla
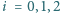 oraz
oraz
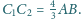 Udowodnij,
że kąt
Udowodnij,
że kąt
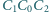 jest prosty i że punkty
jest prosty i że punkty
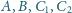 leżą na jednej
płaszczyźnie.
leżą na jednej
płaszczyźnie.

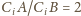 dla
dla
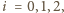 więc wszystkie punkty
więc wszystkie punkty
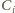 leżą na sferze Apoloniusza dla punktów
leżą na sferze Apoloniusza dla punktów
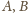 i stałej 2
(zdefiniowanej analogicznie do okręgu). Jej średnicę wyznaczają punkty
i stałej 2
(zdefiniowanej analogicznie do okręgu). Jej średnicę wyznaczają punkty
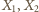 na prostej
na prostej
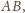 spełniające warunek
spełniające warunek
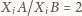 dla
dla
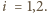 Wówczas
Wówczas
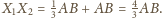
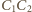 także jest średnicą rozważanej sfery. Stąd
kąt
także jest średnicą rozważanej sfery. Stąd
kąt
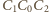 jest prosty, jako wpisany oparty na średnicy. Proste
jest prosty, jako wpisany oparty na średnicy. Proste
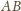 i
i
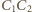 przecinają się (w środku sfery), więc punkty
przecinają się (w środku sfery), więc punkty
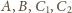 leżą na jednej płaszczyźnie.
leżą na jednej płaszczyźnie.
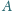 i
i
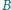 nie należą do płaszczyzny
nie należą do płaszczyzny
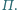 Wyznacz
zbiór wszystkich punktów
Wyznacz
zbiór wszystkich punktów
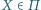 o tej własności, że proste
o tej własności, że proste
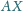 i
i
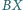 tworzą z płaszczyzną
tworzą z płaszczyzną
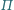 równe kąty.
równe kąty.
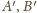 oznaczają odpowiednio rzuty punktów
oznaczają odpowiednio rzuty punktów
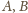 na
płaszczyznę
na
płaszczyznę
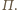 Dla punktu
Dla punktu
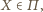 różnego od
różnego od
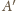 i
i
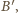 równość
równość
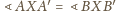 zachodzi wtedy i tylko
wtedy, gdy trójkąty prostokątne
zachodzi wtedy i tylko
wtedy, gdy trójkąty prostokątne
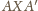 i
i
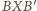 są podobne.
Równoważnie,
są podobne.
Równoważnie,
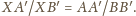 Jeśli
Jeśli
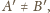 to
punkty
to
punkty
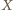 o żądanej własności tworzą okrąg Apoloniusza dla
punktów
o żądanej własności tworzą okrąg Apoloniusza dla
punktów
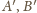 i stałej
i stałej
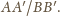 Jakie jest rozwiązanie, gdy
Jakie jest rozwiązanie, gdy
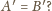 Czy możliwe, by
Czy możliwe, by
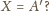
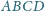 miara kąta wewnętrznego przy wierzchołku
miara kąta wewnętrznego przy wierzchołku
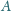 jest większa od
jest większa od
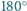 oraz zachodzi równość
oraz zachodzi równość
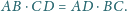 Punkt
Punkt
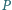 jest symetryczny do punktu
jest symetryczny do punktu
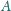 względem prostej
względem prostej
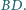 Udowodnij, że
Udowodnij, że
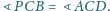
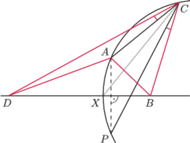
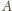 i
i
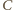 leżą na okręgu Apoloniusza dla punktów
leżą na okręgu Apoloniusza dla punktów
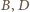 i stałej
i stałej
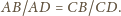 Z symetrii względem prostej
Z symetrii względem prostej
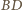 punkt
punkt
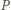 też na nim leży (
też na nim leży (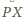 i
i
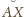 są równe, więc
są równe, więc
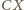 jest dwusieczną kąta
jest dwusieczną kąta
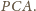 Jednocześnie
Jednocześnie
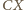 jest też dwusieczną kąta
jest też dwusieczną kąta
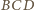 (własność z początku artykułu,
(własność z początku artykułu, 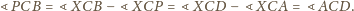
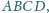 w którym
w którym
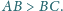 Na boku
Na boku
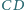 tego prostokąta skonstruuj takie punkty
tego prostokąta skonstruuj takie punkty
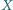 i
i
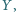 aby
aby
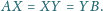
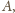 środka boku
środka boku
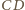 i stałej 2.
i stałej 2.