Odpowiedź: nie.
Uzasadnienie: długość krzywej to kres górny długości linii łamanych w nią wpisanych. Weźmy więc dowolną łamaną, wpisaną w rozważaną krzywą (utworzoną dla pewnego parametru 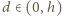 ); jej wierzchołki
); jej wierzchołki 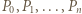 leżą (w takim porządku) na owej krzywej, przy czym
leżą (w takim porządku) na owej krzywej, przy czym 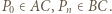 Przedłużenia odcinków
Przedłużenia odcinków 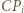 docierają do boku
docierają do boku 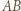 w punktach
w punktach 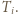 Ustalmy
Ustalmy 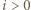 i spójrzmy na czworokąt
i spójrzmy na czworokąt 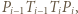 którego boki
którego boki 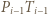 oraz
oraz 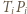 mają długość
mają długość 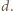 Przyjmijmy, że punkt
Przyjmijmy, że punkt 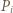 jest nie mniej oddalony od prostej
jest nie mniej oddalony od prostej 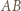 niż punkt
niż punkt 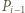 (gdy jest przeciwnie, zamieniamy role wskaźników
(gdy jest przeciwnie, zamieniamy role wskaźników 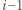 oraz
oraz 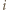 ). Niech punkt
). Niech punkt 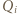 uzupełnia równoległobok
uzupełnia równoległobok 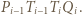 Skoro półproste
Skoro półproste 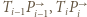 spotykają się (w punkcie
spotykają się (w punkcie 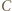 ), odcinek
), odcinek 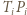 przecina odcinek
przecina odcinek 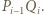 Trójkąt
Trójkąt 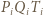 jest równoramienny, jego osią symetrii jest symetralna odcinka
jest równoramienny, jego osią symetrii jest symetralna odcinka 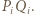 Punkt
Punkt 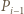 leży po tej stronie owej symetralnej co punkt
leży po tej stronie owej symetralnej co punkt 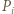 - zatem bliżej punktu
- zatem bliżej punktu 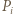 niż punktu
niż punktu 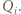 Tak więc
Tak więc 
Taka nierówność zachodzi dla wszystkich 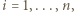 wobec czego łamana
wobec czego łamana 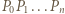 jest krótsza niż bok
jest krótsza niż bok 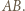 Biorąc kres górny długości wszystkich takich łamanych, wpisanych w rozważaną krzywą, stwierdzamy, że jej długość nie przekracza długości boku
Biorąc kres górny długości wszystkich takich łamanych, wpisanych w rozważaną krzywą, stwierdzamy, że jej długość nie przekracza długości boku 
[Korzystając ze wzoru całkowego na długość krzywej (najwygodniej we współrzędnvch biegunowych ze środkiem 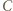 ), nietrudno się przekonać, że długość badanej krzywej jest ściśle malejącą funkcją parametru
), nietrudno się przekonać, że długość badanej krzywej jest ściśle malejącą funkcją parametru 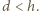 Dla
Dla 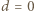 ta krzywa to odcinek
ta krzywa to odcinek 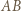 ; dla
; dla 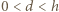 jej długość jest więc ostro mniejsza niż
jej długość jest więc ostro mniejsza niż 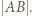 ]
]
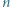 -kąta. Wykazać, że jego wierzchołki można tak pokolorować trzema kolorami, aby każde dwa punkty połączone bokiem lub jedną z narysowanych przekątnych miały różny kolor.
-kąta. Wykazać, że jego wierzchołki można tak pokolorować trzema kolorami, aby każde dwa punkty połączone bokiem lub jedną z narysowanych przekątnych miały różny kolor. -kąta (niekoniecznie wypukłego) nazywamy podział tego wielokąta na
-kąta (niekoniecznie wypukłego) nazywamy podział tego wielokąta na 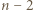 trójkąty przy użyciu pewnej liczby nieprzecinających się przekątnych (które mogą mieć wspólne końce).
trójkąty przy użyciu pewnej liczby nieprzecinających się przekątnych (które mogą mieć wspólne końce). -kąta o tej własności, że w każdym wierzchołku tego trójkąta schodzi się nieparzysta liczba trójkątów tej triangulacji. Wykazać, że
-kąta o tej własności, że w każdym wierzchołku tego trójkąta schodzi się nieparzysta liczba trójkątów tej triangulacji. Wykazać, że  jest liczbą podzielną przez 3.
jest liczbą podzielną przez 3. -kąta (niekoniecznie wypukłego) nazywamy podział tego wielokąta na
-kąta (niekoniecznie wypukłego) nazywamy podział tego wielokąta na 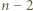 trójkąty przy użyciu pewnej liczby nieprzecinających się przekątnych (które mogą mieć wspólne końce).
trójkąty przy użyciu pewnej liczby nieprzecinających się przekątnych (które mogą mieć wspólne końce).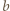 i
i 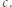
 -kąta należą do trójkątów triangulacji tego samego koloru; bez straty ogólności przypuśćmy, że jest to kolor czarny. Tymczasem każda przekątna triangulacji jest bokiem dokładnie jednego trójkąta czarnego i jednego trójkąta białego. Stąd wniosek, że łączna liczba narysowanych przekątnych jest równa
-kąta należą do trójkątów triangulacji tego samego koloru; bez straty ogólności przypuśćmy, że jest to kolor czarny. Tymczasem każda przekątna triangulacji jest bokiem dokładnie jednego trójkąta czarnego i jednego trójkąta białego. Stąd wniosek, że łączna liczba narysowanych przekątnych jest równa 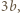 a łączna liczba boków
a łączna liczba boków  -kąta i narysowanych przekątnych jest równa
-kąta i narysowanych przekątnych jest równa 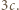 W konsekwencji
W konsekwencji 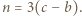
 -kąta, przy czym
-kąta, przy czym 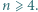 Na czarno malujemy wszystkie trójkąty tej triangulacji, których dokładnie jeden bok jest przekątną danego
Na czarno malujemy wszystkie trójkąty tej triangulacji, których dokładnie jeden bok jest przekątną danego  -kąta, a na biało - wszystkie trójkąty tej triangulacji, których wszystkie trzy boki są przekątnymi danego
-kąta, a na biało - wszystkie trójkąty tej triangulacji, których wszystkie trzy boki są przekątnymi danego  -kąta. Wykazać, że liczba czarnych trójkątów jest o
-kąta. Wykazać, że liczba czarnych trójkątów jest o 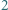 większa od liczby białych trójkątów.
większa od liczby białych trójkątów. -kąta (niekoniecznie wypukłego) nazywamy podział tego wielokąta na
-kąta (niekoniecznie wypukłego) nazywamy podział tego wielokąta na 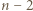 trójkąty przy użyciu pewnej liczby nieprzecinających się przekątnych (które mogą mieć wspólne końce).
trójkąty przy użyciu pewnej liczby nieprzecinających się przekątnych (które mogą mieć wspólne końce).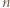 -kąta i oznaczmy przez
-kąta i oznaczmy przez 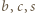 odpowiednio liczby białych, czarnych i szarych trójkątów.
odpowiednio liczby białych, czarnych i szarych trójkątów.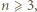 to nie istnieje trójkąt, którego wszystkie boki są także bokami danego
to nie istnieje trójkąt, którego wszystkie boki są także bokami danego  -kąta, więc każdy z
-kąta, więc każdy z 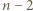 trójkątów został pomalowany dokładnie jednym kolorem, czyli
trójkątów został pomalowany dokładnie jednym kolorem, czyli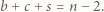
 -kąta, a każdy szary trójkąt ma dokładnie jeden taki bok. Stąd
-kąta, a każdy szary trójkąt ma dokładnie jeden taki bok. Stąd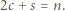
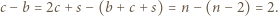
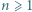 różnych okręgów dzieli płaszczyznę na co najwyżej
różnych okręgów dzieli płaszczyznę na co najwyżej 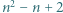 obszarów.
obszarów.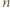 okręgów na płaszczyźnie, to po dorysowaniu jeszcze jednego liczba obszarów wzrośnie o co najwyżej
okręgów na płaszczyźnie, to po dorysowaniu jeszcze jednego liczba obszarów wzrośnie o co najwyżej 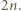
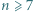 możemy tak umieścić w wierzchołkach
możemy tak umieścić w wierzchołkach  -kąta foremnego różne liczby od
-kąta foremnego różne liczby od 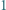 do
do 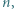 by wartość bezwzględna różnicy liczb z każdych dwóch sąsiednich wierzchołków była kwadratem liczby naturalnej.
by wartość bezwzględna różnicy liczb z każdych dwóch sąsiednich wierzchołków była kwadratem liczby naturalnej.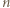 -kątów, w których
-kątów, w których 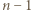 i
i 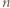 są przypisane sąsiednim wierzchołkom. Krok indukcji o głębokości
są przypisane sąsiednim wierzchołkom. Krok indukcji o głębokości 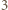 polega na dodaniu trzech wierzchołków z liczbami
polega na dodaniu trzech wierzchołków z liczbami 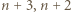 i
i 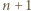 pomiędzy tymi dwoma.
pomiędzy tymi dwoma. jest częścią wspólną sfer
jest częścią wspólną sfer  i
i 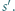 Trzy różne punkty
Trzy różne punkty 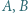 i
i 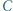 leżą na okręgu
leżą na okręgu  Punkt
Punkt 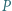 leży na sferze
leży na sferze 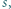 na zewnątrz sfery
na zewnątrz sfery 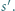 Prosta
Prosta 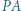 przecina sferę
przecina sferę 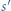 w punkcie
w punkcie 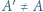 ; analogicznie określamy punkty
; analogicznie określamy punkty 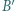 i
i 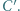 Dowieść, że płaszczyzna
Dowieść, że płaszczyzna 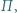 przechodząca przez punkt
przechodząca przez punkt 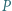 i styczna do sfery
i styczna do sfery 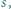 jest równoległa do płaszczyzny
jest równoległa do płaszczyzny 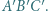
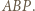 Oznaczmy przez
Oznaczmy przez 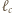 prostą będącą częścią wspólną płaszczyzn
prostą będącą częścią wspólną płaszczyzn 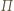 i
i 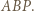 Rachunek na kątach dowodzi, że
Rachunek na kątach dowodzi, że 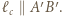 Analogicznie, dla przekroju płaszczyzną
Analogicznie, dla przekroju płaszczyzną 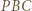 można dowieść, że
można dowieść, że 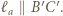
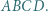 Punkt
Punkt 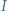 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 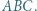 Punkt
Punkt 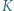 leży na odcinku
leży na odcinku 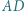 i spełnia warunek
i spełnia warunek
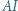 i
i 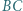 przecinają się w punkcie
przecinają się w punkcie 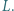 Dowieść, że prosta
Dowieść, że prosta 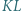 przechodzi przez środek odcinka
przechodzi przez środek odcinka 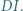
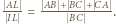 Teraz wystarczy zastosować twierdzenie Menelaosa dla trójkąta
Teraz wystarczy zastosować twierdzenie Menelaosa dla trójkąta 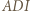 i prostej
i prostej 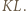
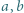 i
i  Wyznaczyć najkrótszą drogę łączącą dwa przeciwległe wierzchołki tego prostopadłościanu, biegnącą po jego powierzchni.
Wyznaczyć najkrótszą drogę łączącą dwa przeciwległe wierzchołki tego prostopadłościanu, biegnącą po jego powierzchni.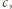 otrzymując z sąsiadujących ścian prostokąt o bokach
otrzymując z sąsiadujących ścian prostokąt o bokach  i
i 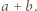 Poszukiwana najkrótsza droga wiedzie po linii prostej, czyli wzdłuż przekątnej tego prostokąta. Jej długość to
Poszukiwana najkrótsza droga wiedzie po linii prostej, czyli wzdłuż przekątnej tego prostokąta. Jej długość to 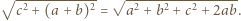 Dwa analogiczne wyniki otrzymamy dla krawędzi
Dwa analogiczne wyniki otrzymamy dla krawędzi 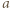 i
i 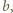 więc powyższa droga jest najkrótsza, jeśli
więc powyższa droga jest najkrótsza, jeśli 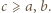
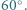 Dowieść, że obwód podstawy tego ostrosłupa jest nie mniejszy od długości każdej jego bocznej krawędzi.
Dowieść, że obwód podstawy tego ostrosłupa jest nie mniejszy od długości każdej jego bocznej krawędzi.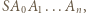 w którym
w którym 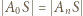 i
i 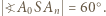 Z tego wynika, że trójkąt
Z tego wynika, że trójkąt 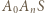 jest równoboczny. Brzeg podstawy ostrosłupa na narysowanej siatce jest łamaną
jest równoboczny. Brzeg podstawy ostrosłupa na narysowanej siatce jest łamaną 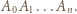
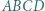 zachodzą równości
zachodzą równości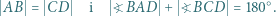
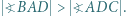
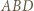 i
i 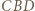 jest trapezem równoramiennym.
jest trapezem równoramiennym.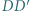 jest wysokością czworościanu
jest wysokością czworościanu 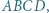 w którym zachodzą równości
w którym zachodzą równości
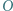 będzie środkiem okręgu opisanego na trójkącie
będzie środkiem okręgu opisanego na trójkącie 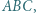 zaś
zaś 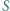 środkiem ciężkości tego trójkąta. Dowieść, że punkty
środkiem ciężkości tego trójkąta. Dowieść, że punkty 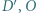 i
i 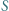 leżą na jednej prostej.
leżą na jednej prostej.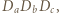 w którym punkty
w którym punkty 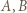 i
i 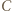 są środkami odcinków odpowiednio
są środkami odcinków odpowiednio 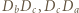 i
i 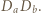 Punkt
Punkt 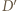 jest ortocentrum trójkąta
jest ortocentrum trójkąta 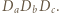 Wystarczy skorzystać z twierdzenia o prostej Eulera.
Wystarczy skorzystać z twierdzenia o prostej Eulera.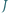 sfery wpisanej oraz środek
sfery wpisanej oraz środek 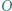 sfery opisanej na czworościanie
sfery opisanej na czworościanie 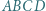 przecina krawędź
przecina krawędź 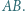 Wykazać, że miary kątów
Wykazać, że miary kątów 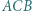 i
i 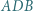 są równe lub sumują się do
są równe lub sumują się do 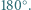
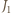 oraz
oraz 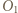 punktów
punktów 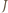 oraz
oraz 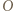 na płaszczyznę
na płaszczyznę 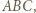 analogicznie
analogicznie 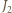 oraz
oraz 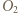 na płaszczyznę
na płaszczyznę 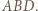 Ponieważ
Ponieważ 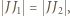 otrzymujemy
otrzymujemy 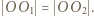 Dalej, z twierdzenia Pitagorasa, okręgi opisane na ścianach
Dalej, z twierdzenia Pitagorasa, okręgi opisane na ścianach 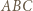 i
i 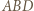 mają równe promienie. Teza wynika z twierdzenia sinusów.
mają równe promienie. Teza wynika z twierdzenia sinusów.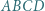 wszystkie wewnętrzne kąty dwuścienne są ostre. Punkt
wszystkie wewnętrzne kąty dwuścienne są ostre. Punkt 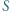 leży wewnątrz tego czworościanu, a jego odległość od każdej z płaszczyzn
leży wewnątrz tego czworościanu, a jego odległość od każdej z płaszczyzn 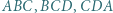 i
i 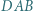 jest większa niż
jest większa niż 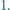 Dowieść, że przynajmniej dwa spośród odcinków
Dowieść, że przynajmniej dwa spośród odcinków 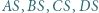 mają długość większą niż
mają długość większą niż 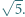
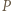 na płaszczyznę
na płaszczyznę 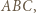 otrzymamy punkt
otrzymamy punkt 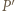 leżący wewnątrz trójkąta
leżący wewnątrz trójkąta 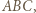 którego odległość od każdego z boków tego trójkąta jest większa od
którego odległość od każdego z boków tego trójkąta jest większa od 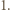 Któryś z kątów trójkąta
Któryś z kątów trójkąta 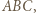 powiedzmy kąt
powiedzmy kąt 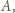 ma miarę nieprzekraczającą
ma miarę nieprzekraczającą 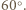 Stąd
Stąd 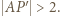 Mamy też
Mamy też 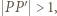 więc z twierdzenia Pitagorasa dla trójkąta
więc z twierdzenia Pitagorasa dla trójkąta 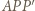 otrzymamy
otrzymamy 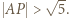 Powtarzając to rozumowanie dla płaszczyzny
Powtarzając to rozumowanie dla płaszczyzny 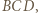 otrzymamy tezę.
otrzymamy tezę.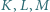 leżą odpowiednio na bokach
leżą odpowiednio na bokach 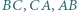 trójkąta
trójkąta 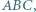 przy czym
przy czym
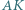 i
i 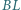 przecinają się w punkcie
przecinają się w punkcie 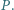 Wykazać, że punkty
Wykazać, że punkty  leżą na jednym okręgu.
leżą na jednym okręgu.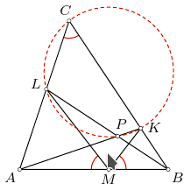
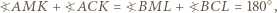
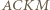 oraz
oraz 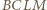 można opisać okręgi. Wobec tego
można opisać okręgi. Wobec tego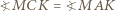
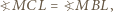
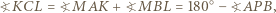
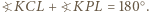
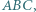 w którym wysokość opuszczona z wierzchołka
w którym wysokość opuszczona z wierzchołka 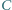 ma długość
ma długość 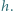 Na każdym odcinku
Na każdym odcinku 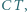 łączącym wierzchołek
łączącym wierzchołek 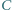 z bokiem
z bokiem 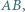 odkładamy odcinek
odkładamy odcinek 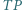 ustalonej długości
ustalonej długości 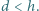 Uzyskane w ten sposób punkty
Uzyskane w ten sposób punkty 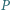 tworzą pewną krzywą. Czy - jeśli liczba
tworzą pewną krzywą. Czy - jeśli liczba 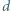 jest dostatecznie mała - długość owej krzywej przekroczy długość boku
jest dostatecznie mała - długość owej krzywej przekroczy długość boku 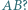
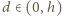 ); jej wierzchołki
); jej wierzchołki 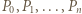 leżą (w takim porządku) na owej krzywej, przy czym
leżą (w takim porządku) na owej krzywej, przy czym 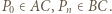 Przedłużenia odcinków
Przedłużenia odcinków 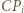 docierają do boku
docierają do boku 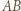 w punktach
w punktach 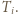 Ustalmy
Ustalmy 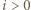 i spójrzmy na czworokąt
i spójrzmy na czworokąt 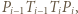 którego boki
którego boki 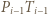 oraz
oraz 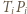 mają długość
mają długość 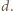 Przyjmijmy, że punkt
Przyjmijmy, że punkt 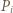 jest nie mniej oddalony od prostej
jest nie mniej oddalony od prostej 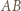 niż punkt
niż punkt 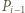 (gdy jest przeciwnie, zamieniamy role wskaźników
(gdy jest przeciwnie, zamieniamy role wskaźników 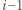 oraz
oraz 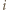 ). Niech punkt
). Niech punkt 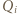 uzupełnia równoległobok
uzupełnia równoległobok 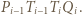 Skoro półproste
Skoro półproste 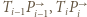 spotykają się (w punkcie
spotykają się (w punkcie 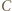 ), odcinek
), odcinek 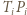 przecina odcinek
przecina odcinek 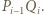 Trójkąt
Trójkąt 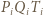 jest równoramienny, jego osią symetrii jest symetralna odcinka
jest równoramienny, jego osią symetrii jest symetralna odcinka 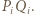 Punkt
Punkt 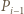 leży po tej stronie owej symetralnej co punkt
leży po tej stronie owej symetralnej co punkt 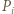 - zatem bliżej punktu
- zatem bliżej punktu 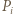 niż punktu
niż punktu 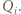 Tak więc
Tak więc 
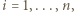 wobec czego łamana
wobec czego łamana 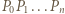 jest krótsza niż bok
jest krótsza niż bok 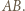 Biorąc kres górny długości wszystkich takich łamanych, wpisanych w rozważaną krzywą, stwierdzamy, że jej długość nie przekracza długości boku
Biorąc kres górny długości wszystkich takich łamanych, wpisanych w rozważaną krzywą, stwierdzamy, że jej długość nie przekracza długości boku 
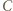 ), nietrudno się przekonać, że długość badanej krzywej jest ściśle malejącą funkcją parametru
), nietrudno się przekonać, że długość badanej krzywej jest ściśle malejącą funkcją parametru 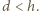 Dla
Dla 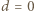 ta krzywa to odcinek
ta krzywa to odcinek 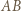 ; dla
; dla 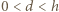 jej długość jest więc ostro mniejsza niż
jej długość jest więc ostro mniejsza niż 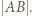 ]
] -kąta wypukłego nie przecinają się w jednym punkcie. Ile jest punktów przecięcia się przekątnych wewnątrz tego wielokąta?
-kąta wypukłego nie przecinają się w jednym punkcie. Ile jest punktów przecięcia się przekątnych wewnątrz tego wielokąta?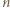 -kąta należy dobrać w parę z czwórką (nieuporządkowaną) wierzchołków
-kąta należy dobrać w parę z czwórką (nieuporządkowaną) wierzchołków  -kąta, które są końcami tych przekątnych.
-kąta, które są końcami tych przekątnych.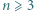 punktów niebieskich leży na wspólnym okręgu. Których wielokątów jest więcej: posiadających wyłącznie niebieskie wierzchołki, czy tych, które posiadają jeden czerwony wierzchołek, a pozostałe niebieskie?
punktów niebieskich leży na wspólnym okręgu. Których wielokątów jest więcej: posiadających wyłącznie niebieskie wierzchołki, czy tych, które posiadają jeden czerwony wierzchołek, a pozostałe niebieskie?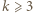 każdy
każdy 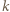 -kąt o niebieskich wierzchołkach parujemy z
-kąt o niebieskich wierzchołkach parujemy z 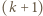 -kątem o jednym wierzchołkiem czerwonym, powstającym przez dołączenie tego wierzchołka. Bez pary pozostaną jedynie trójkąty z czerwonym wierzchołkiem, zatem wielokątów z czerwonym wierzchołkiem jest więcej.
-kątem o jednym wierzchołkiem czerwonym, powstającym przez dołączenie tego wierzchołka. Bez pary pozostaną jedynie trójkąty z czerwonym wierzchołkiem, zatem wielokątów z czerwonym wierzchołkiem jest więcej. -kąt miodowym, jeśli można go rozciąć na sześciokąty foremne o boku 1. Dowieść, że liczba różnych (nieprzystających)
-kąt miodowym, jeśli można go rozciąć na sześciokąty foremne o boku 1. Dowieść, że liczba różnych (nieprzystających) 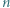 -kątów miodowych nie przekracza
-kątów miodowych nie przekracza 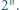
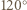 albo
albo 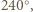 więc ciąg jego kątów jest ciągiem binarnym.
więc ciąg jego kątów jest ciągiem binarnym.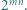
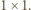 Zbiór czarnych kwadratów
Zbiór czarnych kwadratów 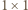 jest podzbiorem zbioru wszystkich
jest podzbiorem zbioru wszystkich 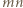 kwadratów
kwadratów 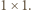
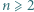 będzie liczbą naturalną. Spośród wierzchołków
będzie liczbą naturalną. Spośród wierzchołków 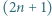 -kąta foremnego wybieramy trzy, które wyznaczają trójkąt rozwartokątny. Na ile sposobów można to zrobić?
-kąta foremnego wybieramy trzy, które wyznaczają trójkąt rozwartokątny. Na ile sposobów można to zrobić?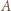 i
i 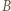 danego
danego 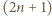 -kąta rysujemy strzałkę
-kąta rysujemy strzałkę 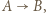 jeśli wędrując po jego obwodzie z
jeśli wędrując po jego obwodzie z 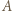 do
do 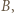 zgodnie z ruchem wskazówek zegara, przejdziemy po co najwyżej
zgodnie z ruchem wskazówek zegara, przejdziemy po co najwyżej  bokach. Z każdego wierzchołka wychodzi
bokach. Z każdego wierzchołka wychodzi  strzałek i tyle samo do każdego wchodzi. Każdy trójkąt rozwartokątny posiada jeden wierzchołek, z którego wychodzą dwie strzałki, i odwrotnie - każde dwie strzałki wychodzące z wspólnego wierzchołka wyznaczają trójkąt rozwartokątny.
strzałek i tyle samo do każdego wchodzi. Każdy trójkąt rozwartokątny posiada jeden wierzchołek, z którego wychodzą dwie strzałki, i odwrotnie - każde dwie strzałki wychodzące z wspólnego wierzchołka wyznaczają trójkąt rozwartokątny.