Dwusieczne»Zadanie 5
o zadaniu...
- Zadanie pochodzi z artykułu Dwusieczne
- Publikacja w Delcie: kwiecień 2016
- Publikacja elektroniczna: 30 marca 2016
- Artykuł źródłowy w wersji do druku [application/pdf]: (84 KB)
Wyznacz środek ciężkości obwodu trójkąta (czyli trójkątnej drucianej ramki).
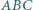 punkty
punkty 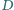 i
i 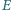 są spodkami dwusiecznych kątów wewnętrznych przy wierzchołkach
są spodkami dwusiecznych kątów wewnętrznych przy wierzchołkach 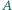 i
i 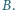 Punkt
Punkt 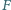 jest spodkiem dwusiecznej zewnętrznej kąta przy wierzchołku
jest spodkiem dwusiecznej zewnętrznej kąta przy wierzchołku 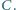 Wykaż, że punkty
Wykaż, że punkty 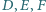 są współliniowe.
są współliniowe.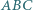 wpisany jest okrąg o promieniu
wpisany jest okrąg o promieniu 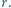 Proste styczne do okręgu i równoległe do boków trójkąta odcinają od niego trzy trójkąty. Wykaż, że suma promieni okręgów wpisanych w te trzy trójkąty jest równa
Proste styczne do okręgu i równoległe do boków trójkąta odcinają od niego trzy trójkąty. Wykaż, że suma promieni okręgów wpisanych w te trzy trójkąty jest równa 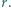

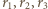 oznaczają odpowiednio promienie okręgów wpisanych w trójkąty
oznaczają odpowiednio promienie okręgów wpisanych w trójkąty 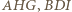 i
i 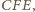 a
a 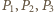 - obwody tych trójkątów. Ponadto niech
- obwody tych trójkątów. Ponadto niech 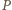 oznacza obwód trójkąta
oznacza obwód trójkąta 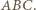
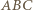 oraz punktów
oraz punktów 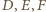 ) otrzymujemy
) otrzymujemy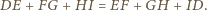
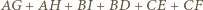
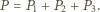
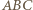 wynika, że dla
wynika, że dla 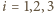 zachodzi równość
zachodzi równość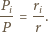
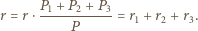
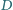 i
i 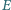 leżą odpowiednio na bokach
leżą odpowiednio na bokach 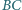 i
i 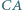 trójkąta
trójkąta 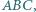 przy czym
przy czym 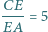 oraz
oraz 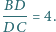 Odcinki
Odcinki 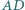 i
i 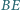 przecinają się w punkcie
przecinają się w punkcie 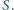 W jakim stosunku punkt
W jakim stosunku punkt 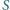 dzieli odcinek
dzieli odcinek 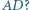
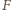 będzie takim punktem na odcinku
będzie takim punktem na odcinku 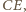 że proste
że proste 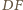 i
i 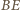 są równoległe. Wówczas z twierdzenia Talesa otrzymujemy
są równoległe. Wówczas z twierdzenia Talesa otrzymujemy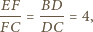
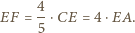
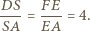
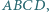 w którym boki
w którym boki 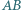 i
i 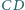 nie są równoległe. Rozważamy okrąg, przechodzący przez punkty
nie są równoległe. Rozważamy okrąg, przechodzący przez punkty 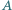 i
i 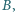 styczny do prostej
styczny do prostej 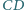 w punkcie
w punkcie 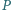 oraz okrąg, przechodzący przez punkty
oraz okrąg, przechodzący przez punkty 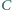 i
i 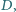 styczny do prostej
styczny do prostej 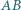 w punkcie
w punkcie 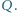 Zakładamy, że punkty
Zakładamy, że punkty 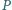 i
i 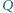 leżą na odcinkach
leżą na odcinkach 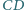 i
i 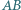 oraz że wspólna cięciwa tych okręgów przechodzi przez środek odcinka
oraz że wspólna cięciwa tych okręgów przechodzi przez środek odcinka 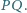 Udowodnić, że proste
Udowodnić, że proste 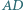 i
i 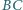 są równoległe.
są równoległe.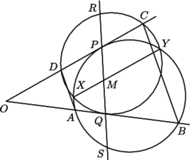
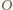 przecięcia prostych
przecięcia prostych 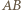 i
i 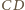 leży na półprostych
leży na półprostych 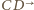 i
i 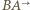 oraz że prosta
oraz że prosta 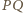 przecina okręgi
przecina okręgi 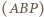 i
i 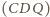 odpowiednio w punktach
odpowiednio w punktach 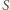 i
i 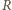 (różnych od
(różnych od 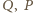 ). Wspólna cięciwa tych okręgów - nazwijmy ją
). Wspólna cięciwa tych okręgów - nazwijmy ją 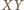 - przechodzi przez środek
- przechodzi przez środek 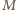 odcinka
odcinka 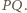 Z równości
Z równości 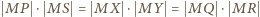 oraz
oraz 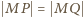 wnosimy, że
wnosimy, że 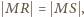 a stąd
a stąd 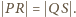
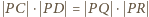 oraz
oraz 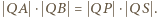 Prawe strony tych równości są równe, więc lewe też. Oznaczając odległości punktów
Prawe strony tych równości są równe, więc lewe też. Oznaczając odległości punktów 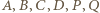 od punktu
od punktu 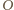 kolejno literami
kolejno literami 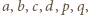 przepisujemy uzyskaną zależność w postaci
przepisujemy uzyskaną zależność w postaci 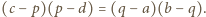 Po wymnożeniu i uwzględnieniu równości
Po wymnożeniu i uwzględnieniu równości 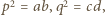 otrzymujemy związek
otrzymujemy związek 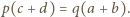 Tak więc
Tak więc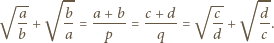
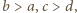 wynika stąd, że
wynika stąd, że 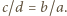 To zaś oznacza, że proste
To zaś oznacza, że proste 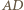 i
i 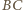 są równoległe.
są równoległe.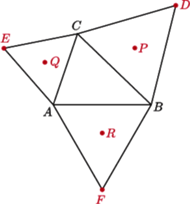
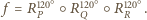 Na mocy
Na mocy 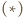 jest to przesunięcie. Ponieważ
jest to przesunięcie. Ponieważ 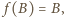 to wektor przesunięcia jest zerowy, czyli
to wektor przesunięcia jest zerowy, czyli 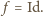 Zatem na mocy
Zatem na mocy 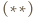 trójkąt
trójkąt 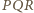 jest równoboczny.
jest równoboczny.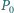 i trójkąt
i trójkąt 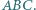 Niech
Niech 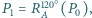
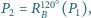
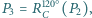
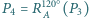 itd. Udowodnij, że jeżeli
itd. Udowodnij, że jeżeli 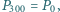 to trójkąt
to trójkąt 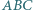 jest równoboczny.
jest równoboczny.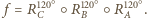 Na mocy
Na mocy 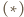 jest to przesunięcie. Z treści zadania wynika, że
jest to przesunięcie. Z treści zadania wynika, że 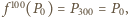 stąd wektor przesunięcia jest zerowy, czyli
stąd wektor przesunięcia jest zerowy, czyli 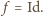 Wobec tego na mocy
Wobec tego na mocy 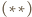 trójkąt
trójkąt 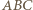 ma kąty równe
ma kąty równe 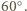
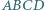 i
i 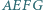 o środkach odpowiednio
o środkach odpowiednio 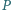 i
i 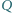 są tak samo zorientowane i mają rozłączne wnętrza. Punkty
są tak samo zorientowane i mają rozłączne wnętrza. Punkty 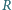 i
i 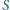 są środkami odpowiednio odcinków
są środkami odpowiednio odcinków 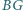 i
i 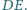 Wykaż, że czworokąt
Wykaż, że czworokąt 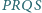 jest kwadratem.
jest kwadratem.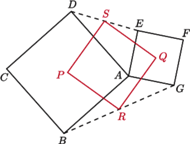
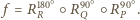 Na mocy
Na mocy 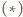 jest to przesunięcie;
jest to przesunięcie; 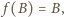 więc
więc 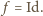 Na mocy
Na mocy 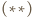 trójkąt
trójkąt 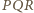 jest prostokątny i
jest prostokątny i 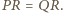 Tak samo dowodzimy, że trójkąt
Tak samo dowodzimy, że trójkąt 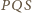 jest drugą połową kwadratu
jest drugą połową kwadratu 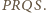
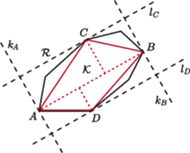
 wybierzmy te dwa, które są najdalej od siebie, i oznaczmy je przez
wybierzmy te dwa, które są najdalej od siebie, i oznaczmy je przez 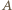 i
i 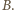 Przez te wierzchołki przeprowadźmy proste
Przez te wierzchołki przeprowadźmy proste 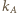 i
i 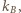 prostopadłe do odcinka
prostopadłe do odcinka 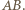 Wówczas
Wówczas 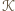 jest zawarty w pasie
jest zawarty w pasie 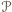 ograniczonym prostymi
ograniczonym prostymi 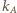 i
i 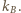 Po obu stronach prostej
Po obu stronach prostej 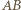 znajdźmy te wierzchołki
znajdźmy te wierzchołki 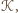 które są najdalej od tej prostej, i nazwijmy je
które są najdalej od tej prostej, i nazwijmy je 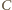 i
i 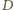 (być może któryś z nich jest wierzchołkiem
(być może któryś z nich jest wierzchołkiem 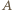 lub
lub 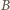 ). Przez
). Przez 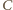 i
i 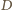 poprowadźmy proste
poprowadźmy proste 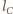 i
i 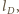 równoległe do
równoległe do 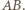 Wielokąt
Wielokąt 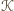 jest zawarty w pasie
jest zawarty w pasie 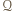 ograniczonym tymi prostymi, jest zatem zawarty w prostokącie
ograniczonym tymi prostymi, jest zatem zawarty w prostokącie 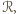 będącym przecięciem pasów
będącym przecięciem pasów 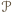 i
i 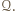 Z konstrukcji wynika, że pole prostokąta
Z konstrukcji wynika, że pole prostokąta 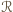 jest dwa razy większe od pola
jest dwa razy większe od pola 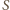 czworokąta
czworokąta 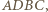 który jest zawarty w
który jest zawarty w 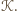 Zatem
Zatem 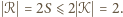
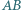 i
i 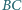 kwadratu
kwadratu 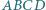 leżą (odpowiednio) takie punkty
leżą (odpowiednio) takie punkty 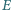 i
i 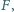 zaś wewnątrz tego kwadratu znajduje się taki punkt
zaś wewnątrz tego kwadratu znajduje się taki punkt 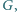 że
że 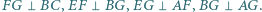 Sporządzony odręcznie rysunek sugeruje, że trapez
Sporządzony odręcznie rysunek sugeruje, że trapez 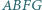 pokrywa około 40% powierzchni kwadratu
pokrywa około 40% powierzchni kwadratu  Czy jest to równość dokładna?
Czy jest to równość dokładna?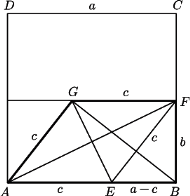
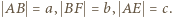 Z podanych warunków wynika, że czworokąt
Z podanych warunków wynika, że czworokąt 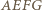 jest równoległobokiem o przekątnych prostopadłych, czyli rombem. Trójkąty
jest równoległobokiem o przekątnych prostopadłych, czyli rombem. Trójkąty 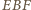 i
i 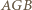 są podobne. Stąd
są podobne. Stąd 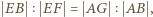 czyli
czyli 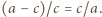 Z tego równania wyznaczamy
Z tego równania wyznaczamy 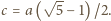 Z trójkąta prostokątnego
Z trójkąta prostokątnego 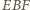 dostajemy
dostajemy 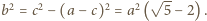 Pole trapezu
Pole trapezu 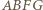 wynosi
wynosi 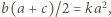 gdzie
gdzie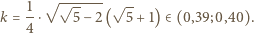
 punkty
punkty  i
i 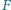 są środkami boków
są środkami boków 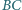 i
i 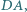 ponadto
ponadto 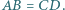 Wykaż, że prosta
Wykaż, że prosta 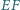 tworzy z prostymi
tworzy z prostymi 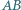 i
i 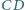 równe kąty.
równe kąty.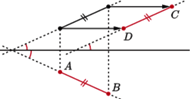
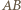 na
na 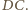 Na mocy
Na mocy 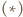 jej osią jest prosta
jej osią jest prosta 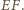 Prosta
Prosta 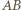 i jej obraz (prosta równoległa do
i jej obraz (prosta równoległa do 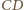 ) tworzą z osią symetrii równe kąty, co kończy dowód.
) tworzą z osią symetrii równe kąty, co kończy dowód.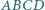 i
i 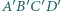 są przeciwnie zorientowane. Udowodnij, że środki odcinków
są przeciwnie zorientowane. Udowodnij, że środki odcinków 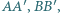
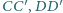 są współliniowe.
są współliniowe.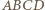 na
na 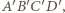 a następnie wykorzystać uwagę (*).
a następnie wykorzystać uwagę (*).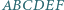 zachodzą równości
zachodzą równości 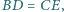
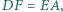
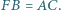 Wykaż, że symetralne boków
Wykaż, że symetralne boków  przecinają się w jednym punkcie.
przecinają się w jednym punkcie.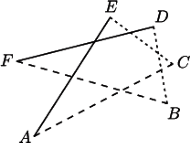
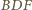 i
i 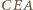 są przystające i tak samo zorientowane, istnieje więc izometria zachowująca orientację, która przeprowadza jeden z nich na drugi. Odcinki
są przystające i tak samo zorientowane, istnieje więc izometria zachowująca orientację, która przeprowadza jeden z nich na drugi. Odcinki 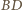 i
i 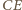 przecinają się, jako przekątne czworokąta wypukłego
przecinają się, jako przekątne czworokąta wypukłego 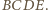 Stąd rozważana izometria jest obrotem; oznaczmy jego środek przez
Stąd rozważana izometria jest obrotem; oznaczmy jego środek przez 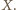
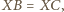 czyli punkt
czyli punkt 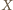 leży na symetralnej odcinka
leży na symetralnej odcinka 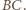 Analogicznie leży też na symetralnych
Analogicznie leży też na symetralnych 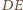 i
i 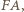 co kończy dowód.
co kończy dowód.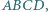 że
że 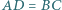 oraz boki
oraz boki 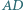 i
i 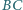 nie są równoległe. Zmienne punkty
nie są równoległe. Zmienne punkty 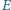 i
i 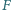 należą odpowiednio do boków
należą odpowiednio do boków 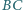 i
i 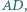 przy czym
przy czym 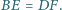 Proste
Proste 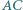 i
i 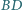 przecinają się w punkcie
przecinają się w punkcie 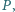 proste
proste 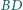 i
i 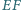 w punkcie
w punkcie 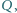 a proste
a proste 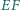 i
i 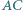 - w punkcie
- w punkcie 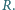 Wykaż, że okręgi opisane na trójkątach
Wykaż, że okręgi opisane na trójkątach 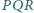 mają wspólny punkt różny od
mają wspólny punkt różny od 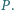
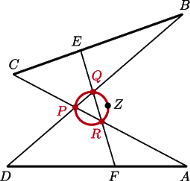
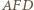 na
na 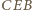 ; oznaczmy jego środek przez
; oznaczmy jego środek przez 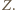 Podobnie jak w rozwiązaniu zadania 3, punkt
Podobnie jak w rozwiązaniu zadania 3, punkt 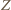 należy do symetralnych odcinków
należy do symetralnych odcinków 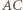 i
i 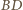 (a więc nie zależy od wyboru punktów
(a więc nie zależy od wyboru punktów 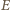 i
i 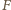 ) oraz do symetralnej
) oraz do symetralnej 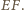 Stąd rzutami punktu
Stąd rzutami punktu 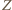 na odcinki
na odcinki 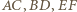 są ich środki.
są ich środki.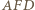 na
na 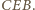 Na mocy (*), środki odcinków
Na mocy (*), środki odcinków 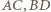 i
i 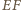 są wówczas współliniowe. Wykazaliśmy, że są to rzuty punktu
są wówczas współliniowe. Wykazaliśmy, że są to rzuty punktu 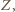 więc korzystając z twierdzenia o prostej Simsona uzyskujemy wniosek, iż stały punkt
więc korzystając z twierdzenia o prostej Simsona uzyskujemy wniosek, iż stały punkt 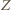 leży na każdym z okręgów opisanych na zmiennych trójkątach
leży na każdym z okręgów opisanych na zmiennych trójkątach 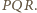
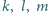 przecinają się w jednym punkcie
przecinają się w jednym punkcie 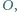 a punkt
a punkt 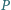 nie należy do żadnej z nich. Punkty
nie należy do żadnej z nich. Punkty 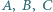 są rzutami prostokątnymi punktu
są rzutami prostokątnymi punktu 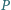 na proste
na proste 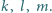 Udowodnij, że rzuty prostokątne
Udowodnij, że rzuty prostokątne 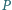 na proste
na proste 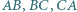 są współliniowe.
są współliniowe.
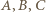 leży na okręgu o średnicy
leży na okręgu o średnicy 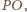 zatem punkt
zatem punkt 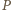 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 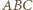 i teza wynika z twierdzenia o prostej Simsona.
i teza wynika z twierdzenia o prostej Simsona.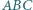 punkty
punkty 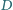 i
i 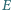 są spodkami wysokości
są spodkami wysokości 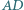 i
i 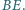 Dwa boki prostokąta
Dwa boki prostokąta 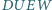 są zawarte w prostych
są zawarte w prostych 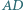 i
i 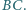 Prosta
Prosta 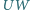 przecina bok
przecina bok 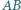 w punkcie
w punkcie 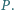 Wykaż, że proste
Wykaż, że proste 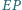 i
i 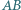 są prostopadłe.
są prostopadłe.
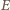 należy do okręgu opisanego na trójkącie
należy do okręgu opisanego na trójkącie 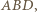 bowiem
bowiem 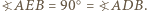 Stąd na mocy twierdzenia o prostej Simsona rzut punktu
Stąd na mocy twierdzenia o prostej Simsona rzut punktu 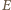 na prostą
na prostą 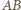 należy do prostej
należy do prostej 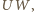 a więc jest nim punkt
a więc jest nim punkt 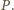
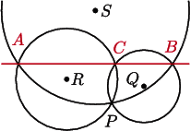
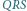
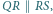
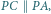
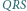
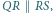
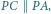
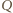 i
i 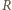 leżą na symetralnej odcinka
leżą na symetralnej odcinka 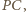 więc rzutem punktu
więc rzutem punktu 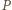 na prostą
na prostą 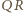 jest środek
jest środek 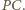 Podobnie dla
Podobnie dla 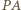 i
i 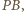 więc rzuty
więc rzuty 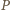 na proste zawierające boki trójkąta
na proste zawierające boki trójkąta 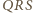 leżą na jednej prostej (równoległej do
leżą na jednej prostej (równoległej do 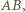 dwukrotnie bliżej punktu
dwukrotnie bliżej punktu 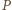 ) i teza wynika z twierdzenia o prostej Simsona.
) i teza wynika z twierdzenia o prostej Simsona.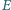 należy do boku
należy do boku 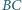 kwadratu
kwadratu 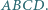 Punkty
Punkty 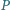 i
i 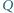 są rzutami prostokątnymi odpowiednio punktów
są rzutami prostokątnymi odpowiednio punktów 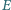 i
i 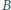 na proste
na proste 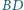 i
i 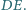 Udowodnij, że punkty
Udowodnij, że punkty 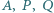 leżą na jednej prostej.
leżą na jednej prostej.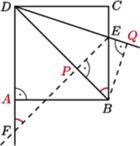
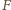 będzie punktem przecięcia prostych
będzie punktem przecięcia prostych 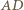 i
i 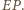 Wówczas
Wówczas 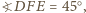 gdyż pozostałe dwa kąty trójkąta
gdyż pozostałe dwa kąty trójkąta 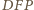 mają
mają 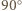 i
i 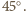 Ponieważ również
Ponieważ również 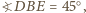 punkty
punkty 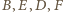 leżą na jednym okręgu. Teza wynika z twierdzenia o prostej Simsona dla trójkąta
leżą na jednym okręgu. Teza wynika z twierdzenia o prostej Simsona dla trójkąta 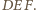
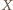 będzie punktem przecięcia dwóch z danych prostych. Pozostałe dwie proste nie są równoległe, stąd dwa trójkąty o wierzchołku
będzie punktem przecięcia dwóch z danych prostych. Pozostałe dwie proste nie są równoległe, stąd dwa trójkąty o wierzchołku 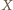 nie są jednokładne, więc opisane na nich okręgi nie są styczne w
nie są jednokładne, więc opisane na nich okręgi nie są styczne w 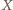 i mają drugi punkt wspólny
i mają drugi punkt wspólny 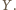
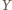 na wszystkie dane proste są współliniowe. Znów na mocy tego twierdzenia, punkt
na wszystkie dane proste są współliniowe. Znów na mocy tego twierdzenia, punkt 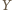 należy wówczas także do pozostałych dwóch z danych okręgów.
należy wówczas także do pozostałych dwóch z danych okręgów.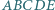 będzie wypukłym pięciokątem wpisanym w półkole o średnicy
będzie wypukłym pięciokątem wpisanym w półkole o średnicy 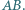 Punkty
Punkty 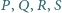 to rzuty punktu
to rzuty punktu 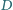 odpowiednio na proste
odpowiednio na proste 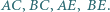 Udowodnij, że proste
Udowodnij, że proste 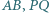 i
i 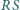 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.