Klub 44M - zadania III 2019»Zadanie 777
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania III 2019
- Publikacja w Delcie: marzec 2019
- Publikacja elektroniczna: 1 marca 2019
- Artykuł źródłowy w wersji do druku [application/pdf]: (385 KB)
W trójkącie 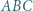 bok
bok 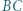 jest najdłuższy. Okrąg wpisany jest styczny do boków
jest najdłuższy. Okrąg wpisany jest styczny do boków 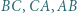 odpowiednio w punktach
odpowiednio w punktach 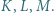 Na prostej
Na prostej 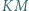 leży taki punkt
leży taki punkt 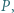 że odcinki
że odcinki 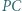 oraz
oraz 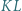 są równoległe. Dowieść, że prosta
są równoległe. Dowieść, że prosta 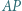 przechodzi przez środek odcinka
przechodzi przez środek odcinka 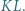
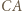 i
i 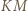 oznaczmy przez
oznaczmy przez 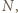 a punkt przecięcia prostych
a punkt przecięcia prostych 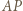 i
i 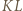 - przez
- przez 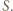 Przyjmijmy ponadto oznaczenia:
Przyjmijmy ponadto oznaczenia: 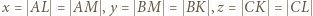 (więc
(więc 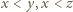 );
); 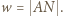 Dzięki równoległości
Dzięki równoległości 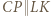 mamy podobieństwa
mamy podobieństwa 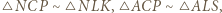 z których wynikają proporcje
z których wynikają proporcje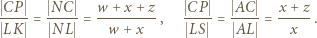
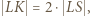 czyli że
czyli że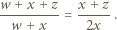
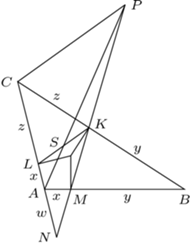
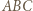 przeciętego prostą
przeciętego prostą 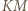 ) daje równość
) daje równość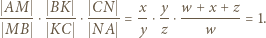
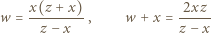
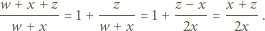
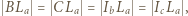 wykonując obliczenia na kątach.
wykonując obliczenia na kątach.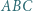 przecinają się w punkcie
przecinają się w punkcie 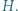 Punkt
Punkt 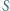 jest środkiem tego łuku
jest środkiem tego łuku 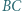 okręgu opisanego na trójkącie
okręgu opisanego na trójkącie 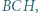 który zawiera punkt
który zawiera punkt 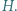 Wyznaczyć miarę kąta
Wyznaczyć miarę kąta 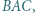 jeśli spełniona jest równość
jeśli spełniona jest równość 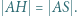
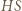 jest dwusieczną
jest dwusieczną 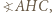 z czego można otrzymać
z czego można otrzymać 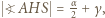 a dalej
a dalej 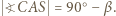 Dodatkowo punkt
Dodatkowo punkt 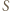 leży na symetralnej odcinka
leży na symetralnej odcinka 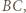 więc jest środkiem okręgu opisanego na trójkącie
więc jest środkiem okręgu opisanego na trójkącie 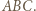
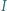 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 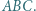 Prosta
Prosta 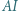 przecina odcinek
przecina odcinek 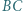 w punkcie
w punkcie 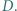 Symetralna odcinka
Symetralna odcinka 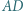 przecina proste
przecina proste 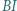 oraz
oraz 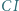 odpowiednio w punktach
odpowiednio w punktach 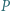 i
i 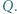 Dowieść, że wysokości trójkąta
Dowieść, że wysokości trójkąta 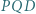 przecinają się w punkcie
przecinają się w punkcie 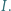
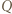 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 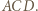 Stąd można wykazać, że
Stąd można wykazać, że 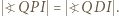
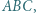 w którym
w którym 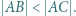 Dwusieczna kąta
Dwusieczna kąta 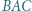 przecina bok
przecina bok 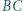 w punkcie
w punkcie 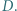 Punkt
Punkt 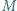 jest środkiem boku
jest środkiem boku 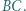 Udowodnić, że prosta przechodząca przez środki okręgów opisanych na trójkątach
Udowodnić, że prosta przechodząca przez środki okręgów opisanych na trójkątach 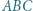 i
i 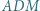 jest równoległa do prostej
jest równoległa do prostej 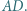
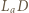 i
i 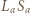 są średnicami okręgów opisanych odpowiednio na trójkątach
są średnicami okręgów opisanych odpowiednio na trójkątach 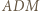 i
i 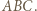
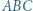 wpisano okrąg o środku
wpisano okrąg o środku 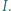 Proste
Proste 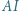 i
i 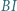 przecinają okrąg opisany na trójkącie
przecinają okrąg opisany na trójkącie 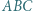 odpowiednio w punktach
odpowiednio w punktach 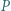 i
i 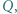 różnych od
różnych od 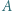 i
i 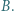 Punkt
Punkt 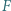 jest takim punktem, że czworokąt
jest takim punktem, że czworokąt 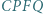 jest równoległobokiem. Dowieść, że jeśli
jest równoległobokiem. Dowieść, że jeśli 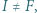 to
to 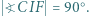
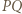 jest symetralną odcinka
jest symetralną odcinka 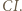 Ponadto trójkąty
Ponadto trójkąty 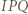 i
i 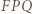 są przystające, co daje
są przystające, co daje 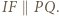
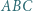 jest styczny do odcinków
jest styczny do odcinków 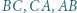 w punktach odpowiednio
w punktach odpowiednio 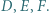 Niech
Niech 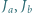 i
i 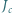 będą odpowiednio środkami okręgów wpisanych w trójkąty
będą odpowiednio środkami okręgów wpisanych w trójkąty 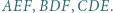 Prosta
Prosta 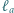 jest symetryczna do prostej
jest symetryczna do prostej 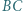 względem prostej
względem prostej 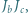 analogicznie określamy proste
analogicznie określamy proste 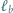 i
i 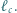 Dowieść, że proste
Dowieść, że proste 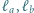 i
i 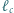 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.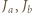 i
i 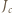 są środkami łuków
są środkami łuków 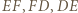 okręgu opisanego na trójkącie
okręgu opisanego na trójkącie 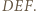 Punkt
Punkt 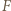 i środek
i środek 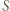 okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt 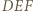 są symetryczne względem prostej
są symetryczne względem prostej 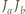 (por. poprzednie zadanie), więc
(por. poprzednie zadanie), więc 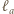 przechodzi przez punkt
przechodzi przez punkt 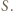
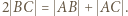 Zastosować twierdzenie Ptolemeusza dla czworokąta
Zastosować twierdzenie Ptolemeusza dla czworokąta 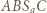 oraz twierdzenie o trójliściu, by wykazać, że punkt
oraz twierdzenie o trójliściu, by wykazać, że punkt 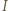 jest środkiem odcinka
jest środkiem odcinka 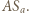
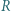 i opisany na trójkącie o promieniu
i opisany na trójkącie o promieniu 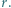 Odległość między środkami tych okręgów jest równa
Odległość między środkami tych okręgów jest równa 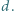 Dowieść, że
Dowieść, że 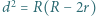 (twierdzenie Eulera).
(twierdzenie Eulera).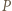 będzie rzutem prostokątnym punktu
będzie rzutem prostokątnym punktu 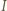 na odcinek
na odcinek 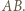 Trójkąty
Trójkąty 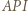 oraz
oraz 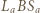 są podobne, więc
są podobne, więc 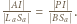 Po zastosowaniu twierdzenia o trójliściu i przekształceniach otrzymamy
Po zastosowaniu twierdzenia o trójliściu i przekształceniach otrzymamy 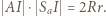 Z drugiej strony,
Z drugiej strony, 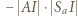 jest potęgą punktu
jest potęgą punktu 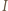 względem okręgu opisanego na trójkącie
względem okręgu opisanego na trójkącie 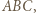 czyli wynosi
czyli wynosi 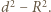
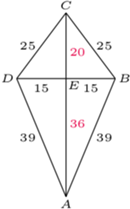
 oraz
oraz 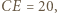 więc
więc 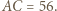
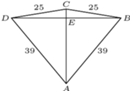
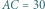
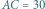
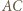 deltoidu może zawierać jego krótszą przekątną (rys. (b)). Wówczas
deltoidu może zawierać jego krótszą przekątną (rys. (b)). Wówczas 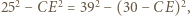 co prowadzi do równości
co prowadzi do równości 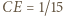 oraz
oraz 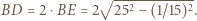
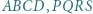 o równych polach i takie, że
o równych polach i takie, że 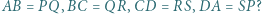

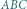
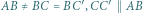
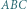
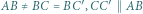
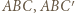 z rysunku mają równe pola i nie są przystające. Niech
z rysunku mają równe pola i nie są przystające. Niech 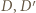 będą obrazami
będą obrazami 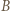 w symetrii odpowiednio względem
w symetrii odpowiednio względem 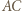 i
i 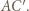 Wówczas deltoidy
Wówczas deltoidy 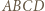 i
i 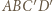 spełniają warunki zadania: mają równe pola i odpowiednie boki oraz nietrudno sprawdzić, że są nieprzystające i wypukłe.
spełniają warunki zadania: mają równe pola i odpowiednie boki oraz nietrudno sprawdzić, że są nieprzystające i wypukłe.
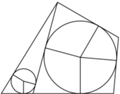
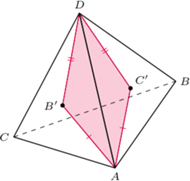
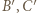 będą punktami styczności sfery wpisanej w czworościan ze ścianami odpowiednio
będą punktami styczności sfery wpisanej w czworościan ze ścianami odpowiednio 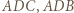 Wówczas
Wówczas 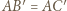 i
i 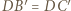 jako odcinki stycznych do tej sfery, więc
jako odcinki stycznych do tej sfery, więc  po rozpłaszczeniu jest deltoidem. Podobnie uzyskujemy pozostałe deltoidy.
po rozpłaszczeniu jest deltoidem. Podobnie uzyskujemy pozostałe deltoidy.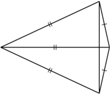
 o osi symetrii
o osi symetrii  i kątach prostych przy
i kątach prostych przy 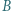 i
i 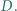 Bila wybita z wierzchołka
Bila wybita z wierzchołka 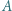 po odbiciu od boku
po odbiciu od boku 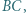 a następnie od
a następnie od 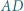 trafia w wierzchołek
trafia w wierzchołek 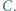 Wykaż, że środek drogi bili leży na
Wykaż, że środek drogi bili leży na 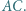
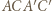 o środku w punkcie
o środku w punkcie 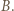 Oznaczmy przez
Oznaczmy przez 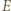 punkt przecięcia drogi bili z odcinkiem
punkt przecięcia drogi bili z odcinkiem 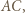 niech
niech 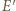 będzie obrazem
będzie obrazem 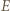 w symetrii względem
w symetrii względem 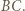 Wystarczy dowieść, że
Wystarczy dowieść, że 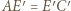 i że odcinki te są równe rozprostowanym odpowiednim fragmentom drogi bili. Przyda się fakt, iż kąt padania bili równy jest kątowi odbicia.
i że odcinki te są równe rozprostowanym odpowiednim fragmentom drogi bili. Przyda się fakt, iż kąt padania bili równy jest kątowi odbicia.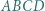 o osi symetrii
o osi symetrii 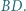 Punkty
Punkty 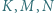 są odpowiednio punktami styczności okręgu wpisanego z bokami
są odpowiednio punktami styczności okręgu wpisanego z bokami 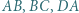 ; proste
; proste 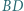 i
i 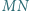 przecinają się w punkcie
przecinają się w punkcie 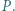 Wykaż, że punkty
Wykaż, że punkty 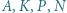 leżą na jednym okręgu.
leżą na jednym okręgu.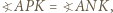 korzystając np. z
korzystając np. z 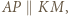 z równoramienności trójkąta
z równoramienności trójkąta 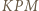 i z twierdzenia o stycznej i cięciwie.
i z twierdzenia o stycznej i cięciwie.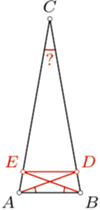
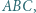 w którym
w którym 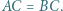 Punkty
Punkty 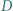 i
i 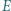 leżą odpowiednio na bokach
leżą odpowiednio na bokach 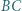 i
i 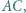 przy czym
przy czym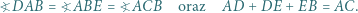
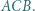
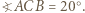
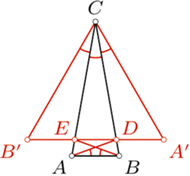
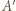 i
i 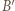 będą punktami symetrycznymi do punktów
będą punktami symetrycznymi do punktów 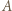 i
i 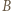 odpowiednio względem prostych
odpowiednio względem prostych 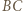 i
i 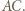 Z danych w treści zadania równości kątów wynika, że punkty
Z danych w treści zadania równości kątów wynika, że punkty 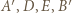 leżą na jednej prostej, a zatem
leżą na jednej prostej, a zatem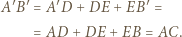
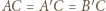 oznacza to, że trójkąt
oznacza to, że trójkąt 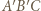 jest równoboczny. W konsekwencji, wobec równości kątów
jest równoboczny. W konsekwencji, wobec równości kątów 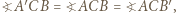 uzyskujemy
uzyskujemy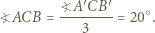
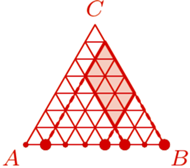
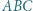 o boku
o boku 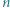 podzielony na
podzielony na 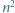 trójkątów równobocznych o boku
trójkątów równobocznych o boku 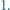 Każdy punkt, który jest wierzchołkiem co najmniej jednego z tych
Każdy punkt, który jest wierzchołkiem co najmniej jednego z tych 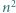 trójkątów, nazwijmy węzłem.
trójkątów, nazwijmy węzłem.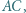 a dwa do
a dwa do 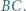
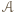 będzie zbiorem
będzie zbiorem 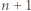 węzłów należących do boku
węzłów należących do boku 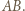
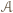 jednoznacznie wyznacza równoległobok o zadanych własnościach, którego punktami przecięcia z
jednoznacznie wyznacza równoległobok o zadanych własnościach, którego punktami przecięcia z 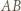 są te cztery punkty i którego "najniższy" wierzchołek nie leży na
są te cztery punkty i którego "najniższy" wierzchołek nie leży na 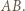 Z kolei każda trójka różnych punktów z
Z kolei każda trójka różnych punktów z 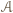 jednoznacznie wyznacza taki równoległobok, którego "najniższy" wierzchołek leży na
jednoznacznie wyznacza taki równoległobok, którego "najniższy" wierzchołek leży na 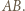
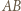 w trzech lub czterech punktach i są to punkty należące do
w trzech lub czterech punktach i są to punkty należące do 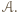 Stąd wniosek, że szukana liczba równoległoboków jest równa łącznej liczbie wyborów trzech lub czterech elementów zbioru
Stąd wniosek, że szukana liczba równoległoboków jest równa łącznej liczbie wyborów trzech lub czterech elementów zbioru 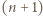 -elementowego, czyli
-elementowego, czyli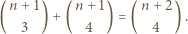
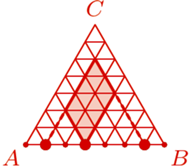
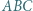 o boku
o boku 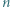 podzielony na
podzielony na 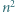 trójkątów równobocznych o boku
trójkątów równobocznych o boku 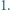 Każdy punkt, który jest wierzchołkiem co najmniej jednego z tych
Każdy punkt, który jest wierzchołkiem co najmniej jednego z tych 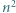 trójkątów, nazwijmy węzłem.
trójkątów, nazwijmy węzłem.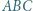 ).
).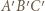 o wierzchołkach w węzłach nazwijmy czapeczką, jeżeli
o wierzchołkach w węzłach nazwijmy czapeczką, jeżeli 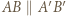 oraz punkty
oraz punkty 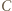 i
i 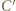 leżą po tej samej stronie prostej
leżą po tej samej stronie prostej 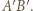
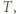 spełniającemu warunki zadania, przyporządkujmy najmniejszą zawierającą go czapeczkę. Precyzyjniej: jeżeli
spełniającemu warunki zadania, przyporządkujmy najmniejszą zawierającą go czapeczkę. Precyzyjniej: jeżeli 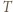 jest czapeczką, to przyporządkowujemy mu siebie samego, natomiast w przeciwnym przypadku - czapeczkę ograniczoną prostymi: równoległą do
jest czapeczką, to przyporządkowujemy mu siebie samego, natomiast w przeciwnym przypadku - czapeczkę ograniczoną prostymi: równoległą do 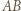 przechodzącą przez wierzchołek
przechodzącą przez wierzchołek 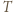 leżący najbliżej
leżący najbliżej 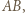 równoległą do
równoległą do 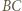 przechodzącą przez wierzchołek
przechodzącą przez wierzchołek 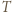 leżący najbliżej
leżący najbliżej 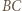 oraz równoległą do
oraz równoległą do 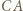 przechodzącą przez wierzchołek
przechodzącą przez wierzchołek 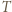 leżący najbliżej
leżący najbliżej 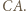
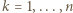 zostało w ten sposób przyporządkowanych dokładnie
zostało w ten sposób przyporządkowanych dokładnie 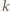 trójkątów spełniających warunki zadania. Co więcej, liczba czapeczek o boku
trójkątów spełniających warunki zadania. Co więcej, liczba czapeczek o boku 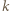 jest równa
jest równa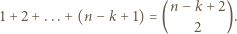
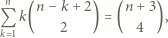
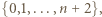 którego drugim co do wielkości elementem jest
którego drugim co do wielkości elementem jest 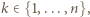 można wybrać na dokładnie
można wybrać na dokładnie 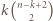 sposobów (wybierając najmniejszy element spośród
sposobów (wybierając najmniejszy element spośród 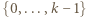 oraz dwa większe od
oraz dwa większe od 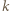 spośród
spośród 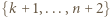 ). Sumując po wszystkich możliwych
). Sumując po wszystkich możliwych 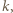 uzyskujemy liczbę sposobów wyboru
uzyskujemy liczbę sposobów wyboru 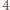 spośród
spośród 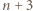 elementów.
elementów.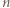 ) oraz w poprzednim (dla trójkąta o boku
) oraz w poprzednim (dla trójkąta o boku 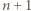 ).
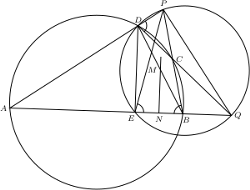
).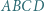 jest wpisany w okrąg. Jego najmniejszy kąt wewnętrzny ma wierzchołek
jest wpisany w okrąg. Jego najmniejszy kąt wewnętrzny ma wierzchołek 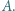 Zakładamy, że proste
Zakładamy, że proste 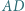 i
i 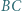 przecinają się w punkcie
przecinają się w punkcie 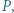 zaś proste
zaś proste 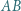 i
i 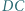 przecinają się w punkcie
przecinają się w punkcie 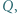 przy czym
przy czym 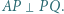 Niech
Niech 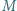 będzie środkiem przekątnej
będzie środkiem przekątnej 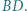 Wykazać, że
Wykazać, że 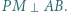
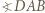 jest najmniejszym kątem czworokąta
jest najmniejszym kątem czworokąta 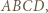 nietrudno wywnioskować, że punkt
nietrudno wywnioskować, że punkt 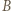 leży między
leży między 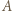 i
i 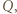 a punkt
a punkt 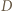 między
między 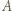 i
i 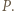 Weźmy pod uwagę okrąg o średnicy
Weźmy pod uwagę okrąg o średnicy 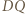 ; ów okrąg przechodzi przez punkt
; ów okrąg przechodzi przez punkt 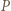 (bo
(bo 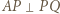 ) oraz przecina odcinek
) oraz przecina odcinek 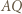 w punkcie, który nazwiemy
w punkcie, który nazwiemy 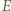 ; zatem
; zatem 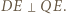
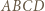 i
i 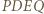 ma okrąg opisany. Wynikają stąd równości kątów
ma okrąg opisany. Wynikają stąd równości kątów 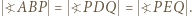 Zatem trójkąt
Zatem trójkąt 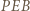 jest równoramienny.
jest równoramienny.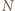 będzie środkiem odcinka
będzie środkiem odcinka 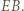 Skoro
Skoro 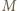 jest środkiem odcinka
jest środkiem odcinka 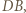 prosta
prosta 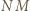 jest równoległa do prostej
jest równoległa do prostej 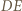 - która jest prostopadła do
- która jest prostopadła do 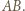 To znaczy, że prosta
To znaczy, że prosta 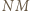 jest symetralną podstawy
jest symetralną podstawy 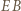 trójkąta równoramiennego
trójkąta równoramiennego 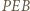 ; przechodzi więc przez punkt
; przechodzi więc przez punkt 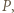 i mamy tezę
i mamy tezę